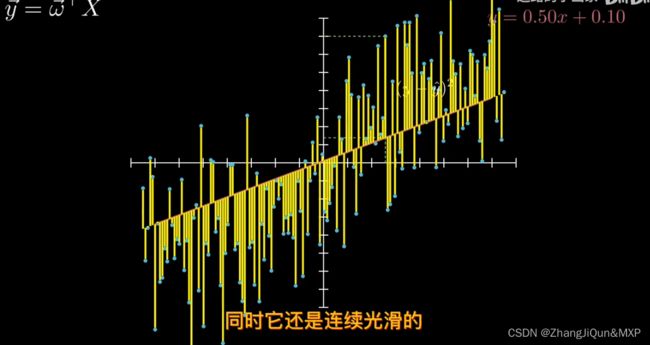
线性回归的正则化改进（岭回归、Lasso、弹性网络），最小二乘法和最大似然估计之间关系，正则化

目录

最小二乘法

极大似然估计的思想

概率：已知分布参数-对分布参数进行估计

概率描述的是结果;似然描述的是假设/模型​编辑

 似然：已知观测结果-对分布参数进行估计​编辑

 对数函数消灭连乘-连乘导致算法参数消失

 极大似然估计公式：将乘法转化为加法增加log​编辑

 最小二乘法=只是极大似然估计在高斯分布下的一种特殊形式​编辑

​极大似然估计就是变化形式最小二乘法

​极大似然估计 就是高斯分布下的特殊形式​编辑

线性回归的正则化改进（岭回归、Lasso、弹性网络）

岭回归的特点

1.正则化（Regularization）

正则化的L1，L2范数

正则化（增加模型参数，不要拟合的太真）

2.归一化 （Normalization）

---

最小二乘法和最大似然估计之间关系

对于最小二乘法，当从模型总体随机抽取n组样本观测值后，最合理的参数估计量应该使得模型能最好地拟合样本数据，也就是估计值和观测值之差的平方和最小。而对于最大似然法，当从模型总体随机抽取n组样本观测值后，最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大。显然，这是从不同原理出发的两种参数估计方法。

在最大似然法中，通过选择参数，使已知数据在某种意义下最有可能出现，而某种意义通常指似然函数最大，而似然函数又往往指数据的概率分布函数。与最小二乘 法不同的是，最大似然法需要已知这个概率分布函数，这在时间中是很困难的。一般假设其满足正态分布函数的特性，在这种情况下，最大似然估计和最小二乘估计相同。

最小二乘法以估计值与观测值的差的平方和作为损失函数，极大似然法则是以最大化目标值的似然概率函数为目标函数，从概率统计的角度处理线性回归并在似然概率函数为高斯函数的假设下同最小二乘建立了的联系。

最小二乘法

 

（1）μ是正态分布的位置参数，描述正态分布的集中趋势位置。正态分布以x = μ 为对称轴，左右完全对称。正态分布的均数、中位数、众数相同，均等于μ . 

（2） σ描述正态分布资料数据分布的离散程度，σ越大，数据分布越分散，σ越小，数据分布越集中。σ也称为是正态分布的形状参数，σ越大，曲线越扁平，反之，σ越小，曲线越瘦高。

极大似然估计的思想

概率：已知分布参数-对分布参数进行估计

概率描述的是结果;似然描述的是假设/模型

 似然：已知观测结果-对分布参数进行估计

 对数函数消灭连乘-连乘导致算法参数消失

 极大似然估计公式：将乘法转化为加法增加log

 最小二乘法=只是极大似然估计在高斯分布下的一种特殊形式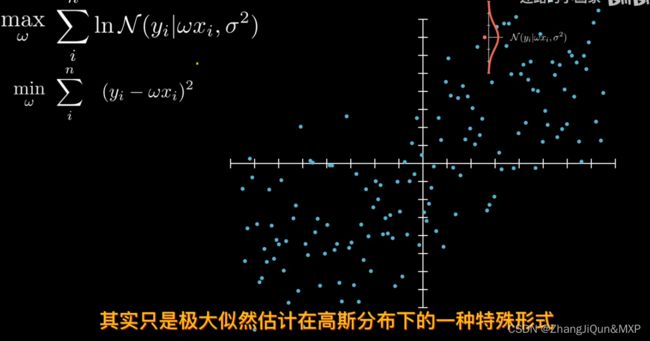

 

 

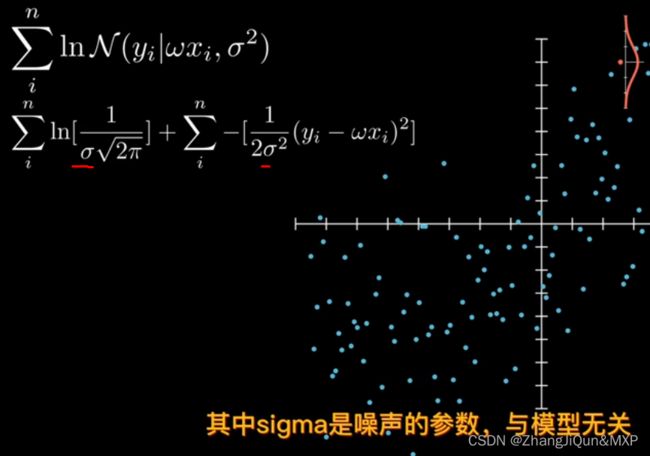 极大似然估计就是变化形式最小二乘法

 极大似然估计 就是高斯分布下的特殊形式

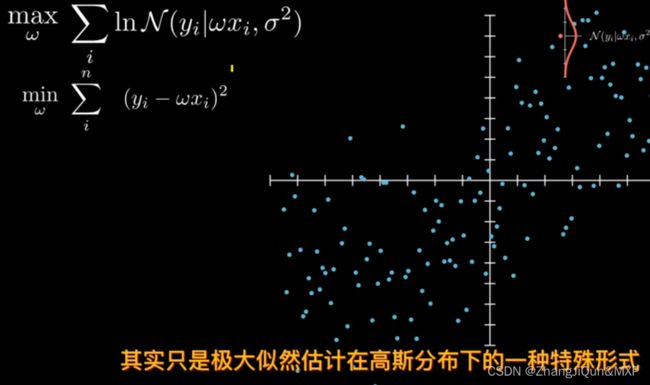
 【机器学习】重新理解线性回归 - 1 - 极大似然估计_哔哩哔哩_bilibili

线性回归的正则化改进（岭回归、Lasso、弹性网络）

 （ElasticNet Regression）。岭回归也叫线性回归的 L2 正则化(平方根函数)，它将系数值缩小到接近零，但不删除任何变量。岭回归可以提高预测精准度，但在模型的解释上会更加的复杂化。

Lasso 回归也叫线性回归的 L1 正则化，该方法最突出的优势在于通过对所有变量系数进行回归惩罚，使得相对不重要的独立变量系数变为 0，从而被排除在建模之外。因此，它在拟合模型的同时进行特征选择。

弹性网络是同时使用了系数向量的L1 范数和L2 范数的线性回归模型，使得可以学习得到类似于Lasso的一个稀疏模型，同时还保留了 Ridge 的正则化属性，结合了二者的优点，尤其适用于有多个特征彼此相关的场合。

岭回归的特点

岭回归是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数，它是更为符合实际、更可靠的回归方法，对存在离群点的数据的拟合要强于最小二乘法。

不同与线性回归的无偏估计，岭回归的优势在于它的无偏估计，更趋向于将部分系数向0收缩。因此，它可以缓解多重共线问题，以及过拟合问题。但是由于岭回归中并没有将系数收缩到0，而是使得系数整体变小，因此，某些时候模型的解释性会大大降低，也无法从根本上解决多重共线问题。

1.正则化（Regularization）

1.1 正则化的目的：我的理解就是平衡训练误差与模型复杂度的一种方式，通过加入正则项来避免过拟合（over-fitting）。（可以引入拟合时候的龙格现象，然后引入正则化及正则化的选取，待添加）

优化定义的加了正则项（也叫惩罚项）的损失函数：　　　　

正则化的L1，L2范数

• L1范数
  当p=1时，是L1范数，其表示某个向量中所有元素绝对值的和。
• L2范数
  当p=2时，是L2范数， 表示某个向量中所有元素平方和再开根， 也就是欧几里得距离公式。

说L1是稀疏的，L2是平滑的？

正则化（增加模型参数，不要拟合的太真）

是一种常用的防止机器学习模型过拟合的技术。过拟合是指模型在训练数据上表现得太好，以至于它不能很好地推广到未见过的数据上。正则化通过引入一个惩罚项来限制模型的复杂度，使得模型在尽可能减小训练误差的同时，也要尽量保持模型的简单。
常见的正则化方法有L1正则化和L2正则化：
1. L1正则化（Lasso回归）：L1正则化将模型的参数权重的绝对值之和作为惩罚项。这意味着模型的某些参数可能会变为零，从而使得模型更稀疏，也就是说模型会依赖于更少的特征。这也使得L1正则化具有特征选择的功能。
2. L2正则化（岭回归）：L2正则化将模型的参数权重的平方和作为惩罚项。这使得模型的参数会被适度地缩小，但是不太可能变为零。这种方法可以防止模型的参数值过大，导致模型过于敏感。
在损失函数中引入这些正则项，模型在训练时不仅要最小化原始的损失函数（如均方误差、交叉熵等），还要尽量使得模型的复杂度（即参数的大小）保持较小。这种权衡使得模型在减小训练误差的同时，也要考虑模型的复杂度，从而防止过拟合。

正则化的选择和调整是一个重要的调参过程，选择合适的正则化方法和参数可以显著地提高模型的泛化性能。

2.归一化 （Normalization）

　　2.1归一化的目的：
　　　　1）归一化后加快了梯度下降求最优解的速度；
　　　　2）归一化有可能提高精度。
　　2.2归一化计算方法　　　　　　
　　公式：
　　　　对于大于1的整数p, Lp norm = sum(|vector|^p)(1/p)
　　2.3.spark ml中的归一化