正则化的线性回归 岭回归、Lasso回归
文章目录
-
-
-
-
- 概述
- 岭回归效果
- Lasso回归效果
- 线性回归效果
-
-
-
概述
正则化的线性回归
岭回归就是正则化的线性回归,线性回归容易出现过拟合,正则化是防止过拟合的常用方法。换句话说是修正后的最小二乘法。
线性回归的误差函数
f ( w ) = 1 2 ∑ i = 1 n ( y − y ‘ ) 2 f(w) = \frac{1}{2}\sum_{i=1}^{n}{(y-y`)^2} f(w)=21i=1∑n(y−y‘)2
优化的误差函数是原来线性回归的均方误差上加上L2范数的惩罚项(修正项),惩罚模型的复杂程度。
f ( w ) = 1 2 ∑ i = 1 n ( y − y ‘ ) 2 + 1 2 a ∗ ∑ j = 1 n w 2 f(w) = \frac{1}{2}\sum_{i=1}^{n}{(y-y`)^2}+\frac{1}{2}a*\sum_{j=1}^{n}{w^2} f(w)=21i=1∑n(y−y‘)2+21a∗j=1∑nw2
Lasso回归也是正则化的线性回归。和岭回归的差别在于修正项取的绝对值
f ( w ) = 1 2 ∑ i = 1 n ( y − y ‘ ) 2 + 1 2 a ∗ ∑ j = 1 n ∣ w ∣ f(w) = \frac{1}{2}\sum_{i=1}^{n}{(y-y`)^2}+\frac{1}{2}a*\sum_{j=1}^{n}{|w|} f(w)=21i=1∑n(y−y‘)2+21a∗j=1∑n∣w∣
岭回归效果
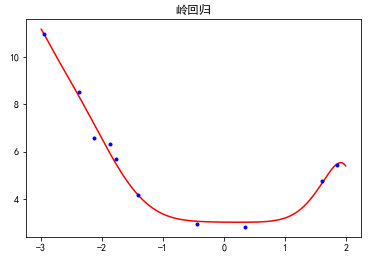
Lasso回归效果
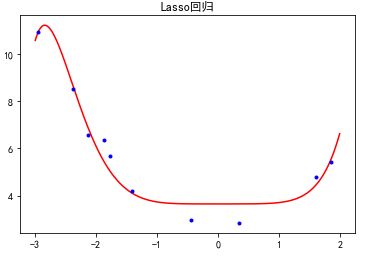
线性回归效果
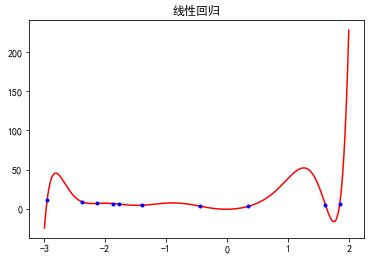
- 多项式特征构造 PolynomialFeatures
如果有a,b两个特征,那么它的2次多项式为(1,a,b,a^2,ab, b^2)
PolynomialFeatures有三个参数
degree:控制多项式的度
interaction_only: 默认为False,如果指定为True,那么就不会有特征自己和自己结合的项,上面的二次项中没有a2和b2。
include_bias:默认为True。如果为True的话,那么就会有上面的 1那一项
例子1,interaction_only为默认的False时
c=[[5,10]] #c=[[a,b]],这里要注意a的shape,如果是list形式,则将a.shape=-1,1
pl=PolynomialFeatures()
b=pl.fit_transform©
b
输出:array([[ 1., 5., 10., 25., 50., 100.]]) #符合(1,a,b,a^2,ab, b^2)
例子2,interaction_only=True时
c=[[5,10]]
pl=PolynomialFeatures(interaction_only=True)
b=pl.fit_transform©
b
输出:array([[ 1., 5., 10., 50.]]) #输出中不包含a^2 和b^2 项