算法练习- 其他算法练习4

xxx

压缩报文还原

• 输入一个压缩后的报文，返回它解压后的原始报文。
• 压缩规则：n[str]，表示方括号内部的 str 重复 n 次。
  注意 n 为正整数（0 < n <= 100），str只包含小写英文字母，不考虑异常情况。

输入：
压缩的报文
输出:
解压后的原始报文

示例一
输入：
3[k]2[mn]
输出
kkkmnmn

示例二
输入
3[m2[c]]
输出
mccmccmcc

示例三
输入
3[m2[cde3[ffgi]]]
输出
mcdeffgiffgiffgicdeffgiffgiffgimcdeffgiffgiffgicdeffgiffgiffgimcdeffgiffgiffgicdeffgiffgiffgi

思路：

• 遍历压缩的报文的每个字符；
• 如果是字母或者数字，则入栈char_digit_stack;
• 如果是$[$则入栈parenth_stack;
• 如果是$]$ 则while parenth_stack: 循环出栈字符和[

python实现：

if __name__ == '__main__':
    s = input().strip()

    char_digit_stack = []
    parenth_stack = []

    result = ""
    # 入栈
    for i in s:
        if i.isdigit() or i.isalpha():
            char_digit_stack.append(i)
        elif i == '[':
            parenth_stack.append(i)
        elif i == "]":
            # 出栈
            temp = ""
            while parenth_stack:
                char = char_digit_stack.pop()
                if char.isalpha():
                    temp = char + temp
                elif char.isdigit():
                    parenth_stack.pop()
                    temp = int(char) * temp

            result += temp

    print(result)

java实现：

import java.util.Scanner;
import java.util.regex.Matcher;
import java.util.regex.Pattern;

public class Main0115 {

  public static final Pattern PATTERN = Pattern.compile("[0-9]+\\[[a-z]+]");

  public static void main(String[] args) {
    try (Scanner scanner = new Scanner(System.in)) {
      String line = scanner.nextLine();
      String res = solution(line);
      System.out.print(res);
    }
  }

  private static String solution(String line) {
    Matcher matcher = PATTERN.matcher(line);
    if (matcher.find()) {
      String group = matcher.group();
      int pos = group.indexOf('[');
      int times = Integer.parseInt(group.substring(0, pos));
      String words = group.substring(pos + 1, group.length() - 1);
      StringBuilder builder = new StringBuilder();
      for (int i = 0; i < times; i++) {
        builder.append(words);
      }
      String fixed = line.replace(group, builder.toString());
      return solution(fixed);
    } else {
      return line;
    }
  }
}

 

符合条件的子串长度

• 给定字符串A、B和正整数V，字符串A和B的长度相等，
• 计算A中满足如下条件的最大连续子串的长度：
  • 该连续子串在A和B中的位置和长度相同。（对应位置截取子串）
  • 该连续子串每个元素差距$|A[i]-B[i]|$（两个字母ASCII码之差的绝对值）之和小于等于V

输入：
第一行输入字符串A，仅包含小写字母，1 <= A.length <= 1000
第二行输入字符串B，仅包含小写字母，1 <= B.length <= 1000
第三行输入正整数V，0 <= V <= 10000

输出：
字符串A 最大连续子串的长度

示例一
输入:
xxcdefg
cdefghi
5
输出:
2

思路：

• 遍历字符串A B的索引（for i in range(n) ），对应A B位置，以每个字符开头的连续子串中，寻找最大长度的；
• 满足子串中对应字符的差值（绝对值）求和 <= V；
• 每次取最大长度；

python实现：

if __name__ == '__main__':
    # xxcdefg
    # cdefghi
    # 5
    # 输入
    s1 = input().strip()
    s2 = input().strip()
    v = int(input().strip())

    n = len(s1)
    max_len = 0
    for i in range(n): # 以每个字符开头的连续子串
        j = i
        sum_ = 0
        while j < n:
            a, b = s1[j], s2[j]
            sum_ += abs(ord(a) - ord(b))
            if sum_ <= v:
                j += 1
            else:
                max_len = max(max_len, j-i)
                break
    print(max_len)

java实现：

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;


public class Main0128 {
  public static void main(String[] args) {
    try (Scanner scanner = new Scanner(System.in)) {
      String a = scanner.nextLine();
      String b = scanner.nextLine();
      int v = scanner.nextInt();
      solution(a, b, v);
    }
  }


  private static void solution(String a, String b, int v) {
    int max = 0;
    int length = 0;
    List<Integer> list = new ArrayList<>();

    list.add(Math.abs(a.charAt(0) - b.charAt(0)));
    int count = list.get(0);

    for (int i = 1; i < a.length(); i++) {

      int temp = Math.abs(a.charAt(i) - b.charAt(i));

      list.add(temp);
      count += Math.abs(temp);

      if (count <= v) {
        length = list.size();
      } else {
        count -= list.get(0);
        list.remove(0);
      }
      max = Math.max(length, max);
    }

    System.out.println(max);
  }
}

 

找单词

• 给一个二维数组和一个字符串，如果该字符串（每个字符）存在于该数组中，则按字符串的字符顺序，输出每个字符所在数组的位置下标，如果找不到，返回字符串。

• 按照字符串的字符顺序搜索，且搜索到的位置必须是相邻的，其中“相邻”是指那些水平相邻或垂直相邻的位置。

• 同一个位置内的字母不允许被重复使用。假定在数组中最多只存在一个可能的匹配。

输入：
第1行 二维数组的行数 n ;
后续n行 大写字符 数组，以 , 分割
最后一行 待查找的字符串，由大写字符组成。
二维数组的大小为N*N，0 < N <= 100。
单词长度K，0 < K < 1000。
输出：
输出位置下标字符串，拼接格式为：第1个字符行下标+“,”+第1个字符列下标+“,”+第2个字符行下标+“,”+第2个字符列下标…+“,”+第N个字符行下标+“,”+第N个字符列下标

示例一
输入：
4
A,C,C,F
C,D,E,D
B,E,S,S
F,E,C,A
ACCESS
输出
0,0,0,1,0,2,1,2,2,2,2,3
说明
ACCESS分别对应二维数组的[0,0] [0,1] [0,2] [1,2] [2,2] [2,3]下标位置

思路：

• 遍历 目标字符串 中的每个字符，逐一在arr二维数值每行中循环查找；
• 查找第一个字符，找到则将（i,j）位置存入idx_list中，并标记flag=True表示当前字符找到，break 查找的循环。
• 查找第二个、三个、… 字符时
  • 若出现一个找不到的（查找循环结束 flag=False），则停止外层字符串的遍历，输出当前字符串（未找到）
  • 若找到位置（i,j），判断是否重复（即是否在idx_list中），重复则从下一行 或者 下一列 的位置继续查找（index(val, j)）；
  • 找到不重复的位置，需要判断是否与上一个位置上下左右连续，是则存入idx_list 并flag=True，结束查找循环。

python实现：

if __name__ == '__main__':
    # 4
    # A, C, C, F
    # C, D, E, D
    # B, E, S, S
    # F, E, C, A
    # ACCESS
    n = int(input().strip())
    arr = []
    for i in range(n):
        arr.append(input().strip().split(","))
    target_word = input().strip()

    # 搜索单词中的每个字符
    idx_list = []
    for char in target_word: # 必须按照顺序查找
        i = 0
        j = 0
        flag = False # 标识某次没有查询到
        print("cur char:", char)
        while i < n: # 搜索
            print("******", i)
            try:
                j = arr[i].index(char, j)
                if (i,j) in idx_list: # 位置不能重复
                    print("11111:", i,j)
                    print("idx list:", idx_list)
                    j += 1
                    if j < n:
                        continue
                    else:
                        raise ValueError(j)
                elif not idx_list:
                    print("2222:", j)
                    idx_list.append((i,j))
                    flag = True
                    break # 结束搜索
                else: # 找到的点是否连续
                    print("33333:", j)
                    pre = idx_list[-1]
                    if (abs(pre[0] - i) == 1 and pre[1] == j) or (abs(pre[1] - j) == 1 and pre[0] == i):
                        print("3333找到连续点", i,j)
                        idx_list.append((i,j))
                        flag = True
                    break

            except ValueError:
                i += 1
                j = 0
        if not flag:
            # 某个字符没找到
            print(target_word)
            break

    # 找到位置
    result = ""
    for i in idx_list:
        i_str = f"{i[0]},{i[1]},"
        result += i_str
    print(result[:-1])

java：

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;


public class Main0100 {
  static List<String> res = new ArrayList<>();

  public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    int N = Integer.parseInt(scanner.nextLine());
    char[][] matrix = new char[N][N];
    for (int i = 0; i < N; i++) {
      matrix[i] = scanner.nextLine()
        .replaceAll(",", "")
        .toCharArray();
    }
    String word = scanner.nextLine();
    scanner.close();

    if (exist(matrix, word)) {
      for (int i = res.size() - 1; i >= 0; i--) {
        System.out.print(res.get(i));
        if (i != 0) {
          System.out.print(",");
        }
      }
    } else {
      System.out.println("N");
    }

  }

  public static boolean exist(char[][] board, String word) {
    int h = board.length, w = board[0].length;
    boolean[][] visited = new boolean[h][w];
    for (int i = 0; i < h; i++) {
      for (int j = 0; j < w; j++) {
        boolean flag = check(board, visited, i, j, word, 0);
        if (flag) {
          res.add(i + "," + j);
          return flag;
        }
      }
    }
    return false;
  }

  public static boolean check(char[][] board,
                              boolean[][] visited,
                              int i, int j, String s, int k) {
    if (board[i][j] != s.charAt(k)) {
      return false;
    } else if (k == s.length() - 1) {
      return true;
    }
    visited[i][j] = true;
    int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
    boolean result = false;
    for (int[] dir : directions) {
      int newi = i + dir[0], newj = j + dir[1];
      if (newi >= 0 && newi < board.length &&
        newj >= 0 && newj < board[0].length) {
        if (!visited[newi][newj]) {
          boolean flag = check(board, visited, newi, newj, s, k + 1);
          if (flag) {
            res.add(newi + "," + newj);
            result = true;
            break;
          }
        }
      }
    }
    visited[i][j] = false;
    return result;
  }
}

 

叠放书籍

书籍的长宽都是整数对应(l, w)
如果书A的长宽度都比B长宽大时，
则允许将B排列放在A上面，
现在有一组规格的书籍，
书籍叠放时要求,书籍不能做旋转，
请计算最多能有多少个规格书籍能叠放在一起。

输入描述
输入:books=[[20,16],[15,11],[10,10],[9,10]]
说明:总共有4本书，第一本长度为20 宽度为16
第一本长度为15 宽度为11
以此类推
最后一本书长度为9 宽度为10
输出描述
输出:3
说明: 最多三个规格的书籍可以叠放在一起 ，
从下到上依次是[20,16],[15,11],[10,10]
示例一
输入
[[20,16],[15,11],[10,10],[9,10]]
输出
3

思路：

• 所有书按照长度降序排序；
• while i< n-1 遍历每一本书，若大于(长度&宽度均大于)后一本书，则 i+=1;
• 否则计算一次最大长度max_len; i+=1; pre=i
• 循环结束时，再计算一次max_len;
• 输出max_len(最小为1)

python实现：

pending...

java:

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;


public class Main0118 {
  public static void main(String[] args) {
    try (Scanner scanner = new Scanner(System.in)) {
      String input = scanner.nextLine();
      solution(input);
    }
  }

  private static void solution(String input) {
    List<Book> books = new ArrayList<>();
    String[] split = input.substring(2, input.length() - 2)
        .split("],\\[");
    for (String book : split) {
      String[] lw = book.split(",");

      int l = Integer.parseInt(lw[0]);
      int w = Integer.parseInt(lw[1]);
      books.add(new Book(l, w));
    }

    books.sort(Book::compareTo);

    int res = counter(books);
    System.out.println(res);


  }

  private static int counter(List<Book> books) {
    int count = 0;
    Book last = null;
    for (Book cur : books) {
      if (last == null) {
        count = 1;
        last = cur;
      } else if (last.l > cur.l && last.w > cur.w) {
        count++;
        last = cur;
      }
    }
    return count;
  }

  private static class Book implements Comparable<Book> {
    int l;
    int w;

    public Book(int l, int w) {
      this.l = l;
      this.w = w;
    }

    @Override
    public int compareTo(Book o) {
      if (this.l >= o.l && this.w >= o.w) {
        return -1;
      } else {
        return o.l - this.l;
      }
    }
  }
}

 

篮球比赛

• 篮球（5v5）比赛中每个球员拥有一个战斗力，所有球员战斗力之和为该队伍的总体战斗力。
• 现有十个球员准备分为两队进行训练赛，希望两个队伍的战斗力差尽可能的小。如何划分？
• 输出分队方案下的最小战斗力差值。

示例一
输入
10 9 8 7 6 5 4 3 2 1
输出
1
说明
1 2 5 9 10 分为一队，3 4 6 7 8 分为一队，两队战斗力之差最小，输出差值1。
备注
球员分队方案不唯一，但最小战斗力差值固定是1

思路：

• 循环五次，每次都为A B 队伍分配一个随机的战斗力；
• 分配完成后，计算两队的战斗力差值，min(min_val, cur_val)
• 以上操作执行1w次，最大概率得到了最小战斗力差值；

python实现：

import random

if __name__ == '__main__':
    s_score = list(map(int, input().strip().split()))

    min_diff = 2**32 - 1
    for i in range(10000):
        temp_score = s_score.copy()
        # a b 队伍的战斗力值
        a = b = 0
        for j in range(5):
            # 随机分配
            n = len(temp_score)
            a += temp_score.pop(random.randint(0, n-1)) # 随机分配一个战斗力
            n = len(temp_score)
            b += temp_score.pop(random.randint(0, n-1)) # random.randint(a,b)包含两边界

        # 一次分配完成，计算最小差值
        min_diff = min(min_diff, abs(a-b))

    print(min_diff)

java:

import java.util.LinkedList; // 底层是链表
import java.util.List; //集合
import java.util.Random;
import java.util.Scanner;


public class Main {
    public static void main(String[] args) {
        try (Scanner scanner = new Scanner(System.in)) {
            String line = scanner.nextLine();
            solution(line);
        }
    }

    private static void solution(String line) {
        String[] split = line.split(" ");

        // 整型的集合
        List<Integer> ints = new LinkedList<>();
        for (String s : split) {
            ints.add(Integer.parseInt(s));
        }

        int min = Integer.MAX_VALUE;
        for (int i = 0; i < 10000; i++) { // 执行1w次 
            // 生产一个随机数对象
            Random random = new Random();
            // 数据复制一份
            List<Integer> tmp = new LinkedList<>(ints); // 集合大小 tmp.size()
            int x = 0, y = 0;
            // 控住分配次数
            for (int j = 0; j < 5; j++) {
                int size = tmp.size(); // 集合大小
                int rd1 = random.nextInt(size); // 0-size之间产生一个随机整数 不含size
                x += tmp.remove(rd1); // 集合删除

                size = tmp.size();
                int rd2 = random.nextInt(size); // 0-size之间产生一个随机整数 不含size
                y += tmp.remove(rd2);
            }
            int diff = Math.abs(x - y); // Math数学计算
            if (diff < min) {
                min = diff;
            }
        }

        System.out.println(min);
    }
}

 

跳格子

• 地上共有N个格子，你需要跳完地上所有的格子，格子间有强依赖关系，跳完前一个格子后，后续的格子才会被开启，格子间的依赖关系由多组steps数组给出。

• steps[0]表示前一个格子，steps[1]表示steps[0]可以开启的格子:
  比如[2,1]，[2,3]表示跳完第2个格子后第1个格子和第3个格子就被开启了

• 计算是否能由给出的steps数组跳完所有的格子，如果可以输出yes，否则输出no

说明：
你可以从一个格子跳到任意一个开启的格子，
没有前置依赖条件的格子默认就是开启的
如果总数是N，则所有的格子编号为[0,1,2,3…N-1]
1 <= N < 500

输入：
整数n表示总共有多少个格子，
输入多组steps表示格子之间的依赖关系

输出:
跳完所有的格子输出yes，否则输出no

示例一
输入
3
0 1
0 2
输出
yes
说明
总共有三个格子[0,1,2]，跳完0个格子后第1个格子就开启了，
跳到第0个格子后第2个格子也被开启了，
按照0->1->2或者0->2->1的顺序都可以跳完所有的格子

示例二
输入
2
1 0
0 1
输出
no
说明
总共有2个格子，第1个格子可以开启第0格子，
但是第1个格子又需要第0个格子才能开启，相互依赖，因此无法完成

示例三
输入
6
0 1
0 2
0 3
0 4
0 5
输出
yes
说明
总共有6个格子，第0个格子可以开启第1,2,3,4,5个格子，
所以跳完第0个格子之后其他格子都被开启了，之后按任何顺序可以跳完剩余的格子

示例四
输入
5
4 3
0 4
2 1
3 2
输出
yes
说明
跳完第0个格子可以开启格子4，跳完格子4可以开启格子3，
跳完格子3可以开启格子2，跳完格子2可以开启格子1，
按照0->4->3->2->1这样就跳完所有的格子

示例五
输入
4
1 2
1 0
输出
yes
说明
总共4个格子[0,1,2,3]，格子1和格子3没有前置条件所以默认开启，
格子1可以开启格子0和格子2，所以跳到格子1之后就可以开启所有的格子，因此可以跳完所有格子

思路：

• 所有格子编号origin集合，去除第二列的格子编号，即为无依赖（默认开启）的格子；
• 将所有默认开启的格子编号放入一个free集合；
• 跳完默认开启的格子，可以打开的格子，依次加入free集合；
• 最后比较origin集合是否等于free集合，是则为yes，否则no;

python：

def judge_walk_all(n, relations):
    # 所有的格子编号
    origin_ids = set(range(n))
    # 可跳的格子
    walk_ids = set()

    # 无依赖（默认开启）的格子编号
    # 获取第二列的格子
    col1, col2 = [], []
    for i in relations:
        col1.append(i[0])
        col2.append(i[1])
    # 默认开启
    free = origin_ids - set(col2)
    free_list = [i for i in col1 if i in free]

    if not free:
        # 没有默认开启的格子，无法开跳
        return "no"
    walk_ids |= free
    while free_list:
        cur_id = free_list.pop()
        try:
            # 根据当前id，获取可以开启的id
            idx = col1.index(cur_id)
            col1[idx] = -1 # 防止下次再次查询到
            open_id = col2[idx]
            free_list.append(open_id)
            walk_ids.add(open_id)
        except ValueError:
            continue
    return "yes" if walk_ids == origin_ids else "no"

# 格式数
n = int(input().strip())
# 循环输入 依赖关系
relations = []
while True:
    s = input().strip()
    if s:
        relations.append(list(map(int, s.split())))
    else:
        break
# 判断是否能走完
result = judge_walk_all(n, relations)
print(result)

java:

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;


public class Main0133 {
  public static List<List<Integer>> list = new ArrayList<>();

  public static void main(String[] args) {
    try (Scanner scanner = new Scanner(System.in)) {
      int n = scanner.nextInt();
      boolean isTrue = true;
      while (scanner.hasNext()) {
        int key = scanner.nextInt();
        if (key == -1) {
          break;
        }
        if (key < 1 && key > n) {
          System.out.println("输入有误");
          return;
        }

        int value = scanner.nextInt();
        if (value < 1 && value > n) {
          System.out.println("输入有误");
          return;
        }

        List<Integer> listChild = new ArrayList<>();
        listChild.add(key);
        listChild.add(value);
        list.add(listChild);
      }

      int len = list.size();
      for (List<Integer> integers : list) {
        if (isBH(integers)) {
          isTrue = false;
          break;
        }
      }

      System.out.println(isTrue ? "yes" : "no");
    }
  }

  public static boolean isBH(List<Integer> listC) {
    for (List<Integer> temp : list) {
      if (temp.get(0).equals(listC.get(listC.size() - 1))) {
        if (listC.contains(temp.get(1))) {
          return true;
        }
        listC.add(temp.get(1));
        isBH(listC);
      }
    }
    return false;
  }
}

 

跳格子2

小明和朋友玩跳格子游戏，有 n 个连续格子组成的圆圈，每个格子有不同的分数，小朋友可以选择以任意格子起跳，但是不能跳连续的格子，不能回头跳，也不能超过一圈;

给定一个代表每个格子得分的非负整数数组，计算能够得到的最高分数。

输入描述
给定一个数例，第一个格子和最后一个格子首尾相连，如: 2 3 2

输出描述
输出能够得到的最高分，如: 3

备注
1≤nums.length≤100
1≤nums[i]≤1000

示例一
输入
2 3 2
输出
3
说明
只能跳3这个格子，因为第一个格子和第三个格子首尾相连

示例二
输入
1 2 3 1
输出
4
说明
1 + 3 = 4

思路：

• 以遍历每个格子，作为start起点；
• 每次走两步，while end - start < n-1：加总分值； end+=2
• while循环结束时，取最大分值；

python:

def rob(nums, start, end):
    pre2, pre1 = 0, 0
    for i in range(start, end + 1):
        cur = max(pre1, pre2 + nums[i])
        pre2 = pre1
        pre1 = cur
    return pre1

nums = list(map(int, input().split()))
if len(nums) == 1:
    print(nums[0])
else:
    print(max(rob(nums, 0, len(nums) - 2), rob(nums, 1, len(nums) - 1)))

java:

package com.amoscloud.nowcoder.refactor.t0251_0260;

import java.util.Scanner;


public class Main0251 {
  public static void main(String[] args) {
    try (Scanner scanner = new Scanner(System.in)) {
      String[] input = scanner.nextLine().split(" ");
      int[] nums = new int[input.length];
      for (int i = 0; i < input.length; i++) {
        nums[i] = Integer.parseInt(input[i]);
      }
      System.out.println(solution(nums));
    }
  }

  public static int solution(int[] nums) {
    if (nums.length == 1) return nums[0];
    return Math.max(rob(nums, 0, nums.length - 2), rob(nums, 1, nums.length - 1));
  }

  private static int rob(int[] nums, int start, int end) {
    int pre2 = 0, pre1 = 0;
    for (int i = start; i <= end; i++) {
      int cur = Math.max(pre1, pre2 + nums[i]);
      pre2 = pre1;
      pre1 = cur;
    }
    return pre1;
  }
}

 

招聘

• 用(S1,E1)、(S2,E2)、(Sj,Ej)…(Si < Ei，均为非负整数)表示每场面试的开始和结束时间。
• 面试采用一对一的方式，面试官完成一次面试后可以立即进行下一场面试，且每个面试官的面试人次不超过m。
• 计算至少需要多少名面试官。

输入：
第一行 面试官的最多面试人次m，
第二行 当天总的面试场次n，
接下来的n行为每场面试的起始时间和结束时间
其中，1 <= n, m <= 500
输出：
至少需要的面试官数量

示例一
输入：
2
5
1 2
2 3
3 4
4 5
5 6
输出：
3
说明
总共有5场面试
且面试时间都不重叠
但每个面试官最多只能面试2人
所以需要3名面试官

示例二
输入
3
3
1 2
2 3
3 4
输出
1
说明
总共有3场面时，面试时间都不重叠
每个面试官最多能面试3人次
所以只需要一名面试官

示例三
输入
3
3
8 35
5 10
1 3
输出
2
说明
总共有3场面时，[5,10]和[8,35]有重叠
所以需要2名面试官

思路：

• 一个场次的开始、结束时间组成一个数组；
• 所有的场次，组成二维数组；
• 使用interviews 数组存储面试官信息
  • [场次的结束时间，场次数] 为一个面试官的信息； 每可以添加一场面试，就将该场面试的结束时间放入第一个位置，当前总场次放入第二个位置；
  • 最后统计interviews数组的长度，得总面试官人数；
  • 当一个面试官的结束时间小于等于另一场次的开始时间时，他才可以在面试人数允许的情况下，接收该场次的面试；否则需要另一个面试官加入interviews数组；

python：

if __name__ == '__main__':
    m = int(input().strip()) # 面试人次
    n = int(input().strip()) # 总场次

    # 接收时间
    times = []
    for i in range(n):
        temp = list(map(int, input().strip().split()))
        times.append(temp)

    # 二维数组排序
    times = sorted(times, key=lambda i:i[0])

    # 面试官的场次分组
    interviews = [[times[0][1], 1],] # 第一个场次的结束时间，面试场次
    # 遍历场次
    for i in range(1, n):
        flag = False # 未成功添加一个场次
        for item in interviews:
            cur_item = item
            # 当前场次的结束时间 小于等于 下一场的开始时间，
            # 则在面试人数允许的情况下，可以添加当前面试场次
            if cur_item[0] <= times[i][0] and cur_item[1] < m:
                # 为当前面试官添加当前场次
                cur_item[1] += 1  # 面试场次+1 （一个人）
                flag = True  # 成功添加一个场次
                cur_item[0] = times[i][1]  # 当前面试官的第一个位置设置为面试场次的结束时间
                # 结束循环，继续下一场面试
                break

        if not flag:
            # 若没有成功添加一个场次，则需要另一个面试官来面试当前场次
            interviews.append([times[i][1], 1])

    # 需要的面试官人数
    print(len(interviews))

java:

import java.util.*;


public class Main0111 {
  public static void main(String[] args) {
    try (Scanner scanner = new Scanner(System.in)) {
      int m = scanner.nextInt();
      int n = scanner.nextInt();
      int[][] arr = new int[n][2];
      for (int i=0;i<n;i++){
        arr[i][0] = scanner.nextInt();
        arr[i][1] = scanner.nextInt();
      }
      solution(m, n, arr);
    }

  }

  private static void solution(int m, int n, int[][] arr) {
    Arrays.sort(arr, Comparator.comparing(c1->c1[0]));
    Deque<int[]> deque = new ArrayDeque<>();
    deque.offer(new int[]{arr[0][1],1});
    for (int i = 1; i < n; i++) {
      boolean flag = false;
      for (int[] p : deque) {
        if (p[0]<= arr[i][0] && p[1]< m){
          p[1]++;
          p[0] = arr[i][1];
          flag = true;
          break;
        }
      }
      if (!flag){
        deque.offer(new int[]{arr[i][1],1});
      }
    }
    System.out.print(deque.size());
  }
}

 

最小传输时延

• 某通信网络中有 N 个网络结点，用 1 到 N 进行标识。网络通过一个有向无环图表示，其中图的边的值表示结点之间的消息传递时延。

• 现给定相连节点之间的时延列表 times[i]={u，v，w}，其中u表示源结点，v表示目的结点，w表示u和v之间的消息传递时延。

• 请计算给定源结点到目的结点的最小传输时延，如果目的结点不可达，输出-1。

N 的取值范围为 [1，100];
时延列表 times 的长度不超过 6000
1≤u,v≤N，0≤w≤100;

输入：
第一行 两个正整数，分别表示网络结点的个数 N，以及时延列表的长度 M，用空格分隔；
接下来的 M 行为两个结点间的时延列表[u v w];
最后一行为两个正整数，分别表示源结点和目的结点。

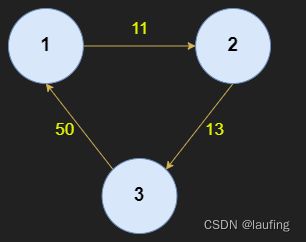
输出：
起点到终点的最小时延，不可达则返回-1。

示例一
输入：
3 3
1 2 11
2 3 13
1 3 50
1 3
输出
24

思路：

• 以字典存储每个节点到其他节点的时延；
• 起始节点到每个节点的最短时延 distances = {1:inf, 2:inf, 3:inf,…};
• 起始节点到自己的时延为设为0；并存入一个temp = [(0, start)]
• 依次计算起始节点到2、3、4…节点的最短时延；
• 每找到距离下一个节点的较短的时延，则将该节点append存入temp->[(dist, next_node)]

python:

def calc_min_dist(nodes, start, end):
    temp = [(0, start)]
    distances = {node: float('infinity') for node in nodes}
    distances[start] = 0

    while temp:
        cur_dist, cur_node = temp.pop()
        if distances[cur_node] < cur_dist: # 最小
            continue
        for next_node, w in nodes[cur_node].items():
            dist = cur_dist + w
            if dist < distances[next_node]:
                distances[next_node] = dist
                temp.append((dist, next_node))
    return distances.get(end, -1)


n, m = map(int, input().split())
nodes = {i: {} for i in range(1, n+1)}
for _ in range(m):
    u, v, w = map(int, input().split())
    nodes[u][v] = w

start, end = map(int, input().split())
result = calc_min_dist(nodes, start, end)

print(int(result) if result != -1 else -1)

java:

import java.util.*;


public class Main0255 {

  public static void main(String[] args) {
    try (Scanner scanner = new Scanner(System.in)) {
      int N = scanner.nextInt();
      int M = scanner.nextInt();
      List<List<int[]>> graph = new ArrayList<>(N + 1);
      for (int i = 0; i <= N; i++) {
        graph.add(new ArrayList<>());
      }

      for (int i = 0; i < M; i++) {
        int u = scanner.nextInt();
        int v = scanner.nextInt();
        int w = scanner.nextInt();
        graph.get(u).add(new int[]{v, w});
      }

      int source = scanner.nextInt();
      int target = scanner.nextInt();
      int result = dijkstra(graph, source, target, N);
      System.out.println(result == Integer.MAX_VALUE ? -1 : result);
    }

  }

  private static int dijkstra(List<List<int[]>> graph, int source, int target, int N) {
    PriorityQueue<int[]> heap = new PriorityQueue<>(Comparator.comparingInt(a -> a[1]));
    heap.offer(new int[]{source, 0});
    boolean[] visited = new boolean[N + 1];
    int[] distance = new int[N + 1];
    Arrays.fill(distance, Integer.MAX_VALUE);
    distance[source] = 0;

    while (!heap.isEmpty()) {
      int[] current = heap.poll();
      int node = current[0];
      int dis = current[1];

      if (node == target) return dis;
      if (visited[node]) continue;

      visited[node] = true;
      for (int[] edge : graph.get(node)) {
        int next = edge[0];
        int nextDis = edge[1] + dis;

        if (nextDis < distance[next]) {
          distance[next] = nextDis;
          heap.offer(new int[]{next, nextDis});
        }
      }
    }

    return Integer.MAX_VALUE;
  }
}