基于小波神经网络的短时交通流量预测Matlab代码

1案例背景

1.1小波理论

        小波分析是针对傅里叶变换的不足发展而来的。傅里叶变换是信号处理领域中应用最广泛的一种分析手段,然而它有一个严重不足,就是变换时抛弃了时间信息,通过变换结果无法判断某个信号发生的时间,即傅里叶变换在时域中没有分辨能力。小波是长度有限、平均为0的波形,它的特点包括:
        1.时域都具有紧支集或近似紧支集;

        2.直流分量为0。
        小波函数是由一个母小波函数经过平移与尺寸伸缩得到,小波分析即把信号分解成一系列小波函数的叠加。小波变换是指把某一基本小波函数ψ(t)平移t后,再在不同尺度α下与待分析的信号r(t)做内积。

        从式(32-1)与式(32-2)可以看出,小波分析能够通过小波基函数的变换分析信号的局部特征,并且在二维情况下具有信号方向选择性能力,因此,该方法作为一种数学理论和分析方法,引起了广泛关注。

1.2小波神经网络

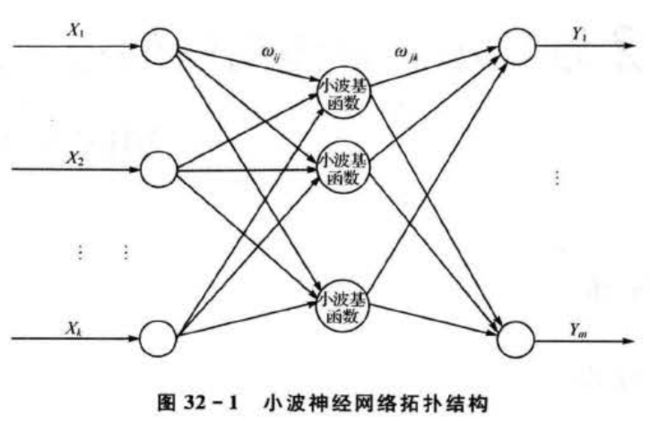
        小波神经网络是一种以BP神经网络拓扑结构为基础,把小波基函数作为隐含层节点的传递函数,信号前向传播的同时误差反向传播的神经网络。小波神经网络的拓扑结构如图32-1所示。

 

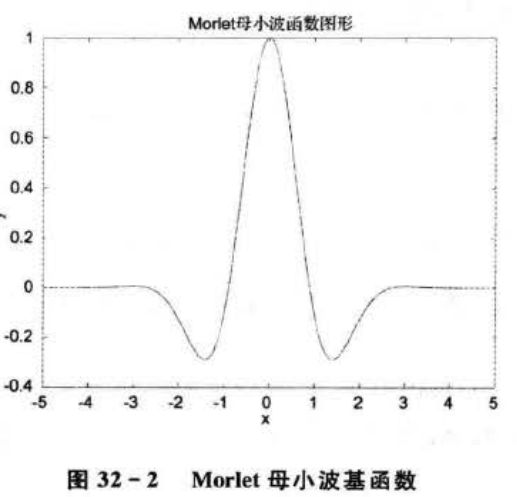
         函数图形如图32 - 2所示

        小波神经网络权值参数修正算法类似于 BP 神经网络权值修正算法 采用梯度修正法修 正网络的权值和小波基函数参数，从而使小波神经网络预测输出不断逼近期望输出 小波神 经网络修正过程如下。

        小波神经网络算法训练步骤如下。
        步骤1:网络初始化。随机初始化小波函数伸缩因子ak、平移因子bk以及网络连接权重wij, wjk,设置网络学习速率η。
        步骤2:样本分类。把样本分为训练样本和测试样本,训练样本用于训练网络,测试样本用于测试网络预测精度。
        步骤3:预测输出。把训练样本输入网络,计算网络预测输出并计算网络输出和期望输出的误差e。
        步骤4:权值修正。根据误差e修正网络权值和小波函数参数,使网络预测值逼近期望值。
        步骤5:判断算法是否结束,若没有结束,返回步骤3。

1.3交通流量预测

        随着交通基础设置建设和智能运输系统的发展,交通规划和交通诱导已成为交通领域研究的热点。对于交通规划和交通诱导来说,准确的交通流量预测是其实现的前提和关键。交通流量预测根据时间跨度可以分为长期交通流量预测和短期交通流量预测:长期交通流量预测以小时,天、月甚至年为时间单位,是宏观意义上的预测;短时交通流量预测一般的时间跨度不超过15分钟,是微观意义上的预测。短时交通流量预测是智能运输系统的核心内容,智能运输系统中多个子系统的功能实现都以其为基础。短时交通流量预测具有高度非线性和不确定性等特点,并且同时间相关性较强,可以看成是时间序列预测问题,比较常用的方法包括多元线性回归预测、AR模型预测、ARMA模型预测、指数平滑预测等。

2模型建立

        研究表明,城市交通路网中交通路段上某时刻的交通流量与本路段前几个时段的交通流量有关,并且交通流量具有24小时内准周期的特性。根据交通流量的特性设计小波神经网络,该网络分为输人层、隐含层和输出层三层。其中,输入层输入为当前时间点的前n个时间点的交通流量;隐含层节点由小波函数构成;输出层输出当前时间点的预测交通流。
        首先采集4天的交通流量数据,每隔15分钟记录一次该段时间内的交通流量，一共记录384个时间点的数据,用3天共288个交通流量的数据训练小波神经网络,最后用训练好的小波神经网络预测第4天的交通流量。基于小波神经网络的短时交通流量预测算法流程如图32-3所示。

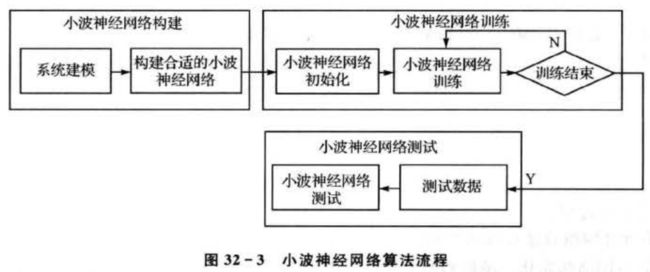
        小波神经网络的构建确定小波神经网络结构。本案例采用的小波神经网络结构为4一6—1:输入层有4个节点,表示预测时间节点前4个时间点的交通流量;隐含层有6个节点;输出层有1个节点,为网络预测的交通流量。网络权值和小波基函数在参数初始化时随机得到。
        小波神经网络训练:用训练数据训练小波神经网络,网络反复训练100次。
        小波神经网络测试:用训练好的小波神经网络预测短时交通流量,并对预测结果进行分析。

3 编程实现

        根据小波神经网络原理在MATLAB环境中编程实现基于小波神经网络的短时交通流量预测，代码如下：

%% 该代码为基于小波神经网络的交通流预测代码

%% 清空环境变量
clc
clear

%% 网络参数配置
load traffic_flux input output input_test output_test

M=size(input,2); %输入节点个数
N=size(output,2); %输出节点个数

n=6; %隐形节点个数
lr1=0.01; %学习概率
lr2=0.001; %学习概率
maxgen=100; %迭代次数

%权值初始化
Wjk=randn(n,M);Wjk_1=Wjk;Wjk_2=Wjk_1;
Wij=randn(N,n);Wij_1=Wij;Wij_2=Wij_1;
a=randn(1,n);a_1=a;a_2=a_1;
b=randn(1,n);b_1=b;b_2=b_1;

%节点初始化
y=zeros(1,N);
net=zeros(1,n);
net_ab=zeros(1,n);

%权值学习增量初始化
d_Wjk=zeros(n,M);
d_Wij=zeros(N,n);
d_a=zeros(1,n);
d_b=zeros(1,n);

%% 输入输出数据归一化
[inputn,inputps]=mapminmax(input');
[outputn,outputps]=mapminmax(output'); 
inputn=inputn';
outputn=outputn';

error=zeros(1,maxgen);
%% 网络训练
for i=1:maxgen
    
    %误差累计
    error(i)=0;
    
    % 循环训练
    for kk=1:size(input,1)
        x=inputn(kk,:);
        yqw=outputn(kk,:);
   
        for j=1:n
            for k=1:M
                net(j)=net(j)+Wjk(j,k)*x(k);
                net_ab(j)=(net(j)-b(j))/a(j);
            end
            temp=mymorlet(net_ab(j));
            for k=1:N
                y=y+Wij(k,j)*temp;   %小波函数
            end
        end
        
        %计算误差和
        error(i)=error(i)+sum(abs(yqw-y));
        
        %权值调整
        for j=1:n
            %计算d_Wij
            temp=mymorlet(net_ab(j));
            for k=1:N
                d_Wij(k,j)=d_Wij(k,j)-(yqw(k)-y(k))*temp;
            end
            %计算d_Wjk
            temp=d_mymorlet(net_ab(j));
            for k=1:M
                for l=1:N
                    d_Wjk(j,k)=d_Wjk(j,k)+(yqw(l)-y(l))*Wij(l,j) ;
                end
                d_Wjk(j,k)=-d_Wjk(j,k)*temp*x(k)/a(j);
            end
            %计算d_b
            for k=1:N
                d_b(j)=d_b(j)+(yqw(k)-y(k))*Wij(k,j);
            end
            d_b(j)=d_b(j)*temp/a(j);
            %计算d_a
            for k=1:N
                d_a(j)=d_a(j)+(yqw(k)-y(k))*Wij(k,j);
            end
            d_a(j)=d_a(j)*temp*((net(j)-b(j))/b(j))/a(j);
        end
        
        %权值参数更新      
        Wij=Wij-lr1*d_Wij;
        Wjk=Wjk-lr1*d_Wjk;
        b=b-lr2*d_b;
        a=a-lr2*d_a;
    
        d_Wjk=zeros(n,M);
        d_Wij=zeros(N,n);
        d_a=zeros(1,n);
        d_b=zeros(1,n);

        y=zeros(1,N);
        net=zeros(1,n);
        net_ab=zeros(1,n);
        
        Wjk_1=Wjk;Wjk_2=Wjk_1;
        Wij_1=Wij;Wij_2=Wij_1;
        a_1=a;a_2=a_1;
        b_1=b;b_2=b_1;
    end
end

%% 网络预测
%预测输入归一化
x=mapminmax('apply',input_test',inputps);
x=x';
yuce=zeros(92,1);
%网络预测
for i=1:92
    x_test=x(i,:);

    for j=1:1:n
        for k=1:1:M
            net(j)=net(j)+Wjk(j,k)*x_test(k);
            net_ab(j)=(net(j)-b(j))/a(j);
        end
        temp=mymorlet(net_ab(j));
        for k=1:N
            y(k)=y(k)+Wij(k,j)*temp ; 
        end
    end

    yuce(i)=y(k);
    y=zeros(1,N);
    net=zeros(1,n);
    net_ab=zeros(1,n);
end
%预测输出反归一化
ynn=mapminmax('reverse',yuce,outputps);

%% 结果分析
figure(1)
plot(ynn,'r*:')
hold on
plot(output_test,'bo--')
title('预测交通流量','fontsize',12)
legend('预测交通流量','实际交通流量','fontsize',12)
xlabel('时间点')
ylabel('交通流量')

        其中,程序中包含的小波函数mymorlet 及小波函数偏导数d_mymorlet的形式如下:
        mymorlet.m文件为：

function y=mymorlet(t)

y = exp(-(t.^2)/2) * cos(1.75*t);

        d_mymorlet.m文件为：

function y=d_mymorlet(t)

y = -1.75*sin(1.75*t).*exp(-(t.^2)/2)-t* cos(1.75*t).*exp(-(t.^2)/2) ;

        运行结果如下：


         从预测结果可以看出，小被神经网络能够比较精确地预测短时交通流量，网络预测值接近期望值。

4案例拓展

        小波神经网络的权值和参数修正采用梯度学习算法，进化缓慢并且容易陆人最小，可以采 用增加动量项的方法提高网络学习效率，增加动量项的权值和参 数修 正公式为

5.完整代码和数据文件

        完整代码和数据文件可以从这里下载：

【免费】基于小波神经网络的短时交通流量预测Matlab代码