DNQ算法原理(Deep Q Network)
![]()
1.强化学习概念
学习系统没有像很多其它形式的机器学习方法一样被告知应该做出什么行为
必须在尝试了之后才能发现哪些行为会导致奖励的最大化
当前的行为可能不仅仅会影响即时奖励,还会影响下一步的奖励以及后续的所有奖励
每一个动作(action)都能影响代理将来的状态(state)
通过一个标量的奖励(reward)信号来衡量成功
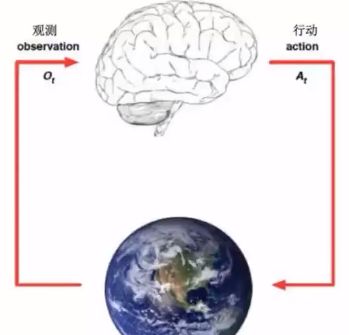
目标:选择一系列行动来最大化未来的奖励
具体的过程就是先观察,再行动,再观察....
状态(state)
Experience is a sequence of observations, actions, rewards.
The state is a summary of experience.
2.马尔科夫决策
马尔科夫决策要求:
-
能够检测到理想的状态
-
可以多次尝试
-
系统的下个状态只与当前状态信息有关,而与更早之前的状态无关,在决策过程中还和当前采取的动作有关
马尔科夫决策过程由5个元素构成:
S:表示状态集(states)
A:表示一组动作(actions)
P:表示状态转移概率P。表示在当前s∈S状态下,经过a∈A作用后,会转移到的其他状态的概率分布情况,在状态s下执行动作a,转移到s'的概率可以表示为p(s|s,a)
R:奖励函数(reward function)表示agent采取某个动作后的即时奖励
y:折扣系数意味着当下的reward比未来反馈的reward更重要
状态价值函数:v(s)=E[Ut|St=s]
t时刻的状态s能获得的未来回报的期望
价值函数用来衡量某一状态或状态 - 动作对的优劣价,累计奖励的期望
最优价值函数:所有策略下的最优累计奖励期望v (s)=max v.(s)
策略:己知状态下可能产生动作的概率分布
3.Bellman方程
Bellman方程:当前状态的价值和下一步的价值及当前的奖励(Reward)有关
价值函数分解为当前的奖励和下一步的价值两部分
这个过程通常采用迭代法实现,每一次迭代都会更新一次状态的值函数,直到收敛为止
值迭代求解:
值迭代是一种求解Bellman方程的方法,其基本思想是通过不断迭代更新状态的值函数,直到收敛到最优解。具体步骤如下:
-
初始化值函数V(s)为0,或者任意一个非负值。
-
对于每个状态s,按照以下公式更新值函数:
V(s) = max{R(s, a) + γ * V(next_state)},其中a为状态s的一个动作,next_state为动作a对应的下一个状态,γ为折扣因子。 3. 重复步骤2,直到值函数收敛到最优解。
值迭代的时间复杂度为O(NT^2),其中N为状态数,T为迭代次数。值迭代的优点是计算量较小,缺点是只能找到局部最优解,而无法保证全局最优解。
前提是安装一下gym
pip install一下就可以了
import numpy as np
import sys
from gym.envs.toy_test import discrete
UP = 0
RIGHT = 1
DOWN = 2
LEFT = 3
class CridworldEnv(discrete.DiscreteEnv):
metadata = {'render.modss':['humin','ansi']}
def __init__(self, shape=[4,4]):
if not isinstance(shape, (list, tuple)) or not len[shape] == 2:
raise ValueError('shape argument must be a list/tuple of length 2')
self.shape = shape
# 定义状态空间、动作空间、转移概率和即时奖励
state_space = [0, 1, 2, 3, 4]
action_space = [0, 1, 2, 3]
transition_probabilities = {
(0, 0): [0.5, 0.5],
(0, 1): [0.5, 0.5],
(1, 0): [0.1, 0.8, 0.1],
(1, 1): [0.8, 0.1, 0.1],
(2, 0): [0.5, 0.5],
(2, 1): [0.5, 0.5],
(3, 0): [0.8, 0.1, 0.1],
(3, 1): [0.1, 0.8, 0.1],
(4, 0): [0.5, 0.5],
(4, 1): [0.5, 0.5]
}
reward_matrix = {
(0, 0): [-1, -1],
(0, 1): [10, -1],
(0, 2): [-1, 10],
(1, 0): [-1, -1],
(1, 1): [-1, -1],
(1, 2): [-1, -1],
(2, 0): [-1, -1],
(2, 1): [10, -1],
(2, 2): [-1, 10],
(3, 0): [-1, -1],
(3, 1): [-1, -1],
(3, 2): [-1, -1],
(4, 0): [-1, -1],
(4, 1): [-1, -1]
}
# 定义值函数初始值和折扣因子
V = {s: 0 for s in state_space}
gamma = 0.9
# 值迭代求解
T = 1000 # 迭代次数
for t in range(T):
for s in state_space:
Q = {a: 0 for a in action_space}
for a in action_space:
for next_s in state_space:
Q[a] += transition_probabilities[(s, a)][next_s] * (reward_matrix[(s, a)][next_s] + gamma * V[next_s])
V[s] = max(Q.values())
# 输出最优值函数和最优策略
print("Optimal value function:")
for s in state_space:
print("V(%d) = %f" % (s, V[s]))
print("Optimal policy:")
for s in state_space:
max_action = argmax(Q.items(), key=lambda x: x[1])[0]
print("Policy for state %d: take action %d" % (s, max_action))手写案例:
import numpy
from gridworld import GridworldEnv
env = GridworldEnv()
def value_iteration(env, theta=0.0001,discount_factor = 1.0):
def one_setp_lookahead(state, v):
A = np.roros(env.nA)
#更新值
for a in range(env.nA):
for prob,next_state,reward,done in env.P[state][a]:
A[a] += ropb*(reward + discount_factor*v[next_state])
return A
w = np.reros(env.nS)
#进行一个迭代更新
while True:
delta = 0
for s in range(env.nS):
# Do a one step lookahead to find the best action
A = one_step_lookahead(s,v)
# Calculate delta across all states seen so far
best_action_value = np.max(A)
# Update the value function
delta = max(delta,np.abs(best_action_value-v[s]))
v[s] = best_action_value
# Check if we can stop
if delta < theta:
break
policy = np.zeros((env.nS,env.nA))
for s in range(env.nS):
A = one_step_lookahead(s,v)
best_action_value = np.max(A)
policy[s,best_action_value] = 1.0
return policy,v
policy, v = value_iteration(env)
print("Policy Probability Distribution")
print(policy)
print("")
print("Reshaped Grid Policy (0=up, 1=right, 2=down, 3=left):")
print(np.reshape(np.argmax(policy, axis=1), env.shape))
print("")4.Q-learning
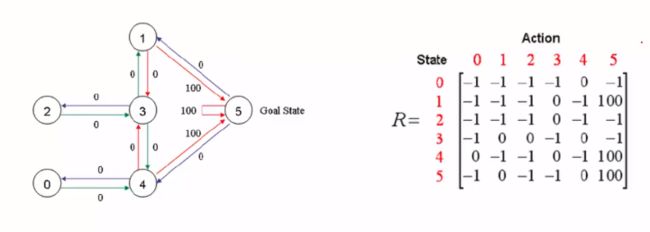
针对图例的形式,我们想要走到5号Goal State,我们要给靠近5的几条路径上加上一些分数奖励,这样才能吸引智能体靠近,并获取达到最后的目的。
Q-learning是强化学习的主要算法之一,是一种无模型的学习方法。它基于一个关键假设,即智能体和环境的交互可看作为一个Markov决策过程(MDP),根据智能体当前所处的状态和所选择的动作,决定一个固定的状态转移概率分布、下一个状态、并得到一个即时回报。Q-learning的目标是寻找一个策略可以最大化将来获得的报酬。
Q-learning的内在思想是通过一个价值表格或价值函数来选取价值最大的动作。Q(s,a)表示在某一具体初始状态s和动作a的情况下,对未来收益的期望值。Q-Learning算法维护一个Q-table,Q-table记录了不同状态下s(s∈S),采取不同动作a(a∈A)的所获得的Q值。在探索环境之前,初始化Q-table,当智能体与环境交互的过程中,算法利用贝尔曼方程来迭代更新Q(s,a),每一轮结束后就生成了一个新的Q-table。智能体不断与环境进行交互,不断更新这个表格,使其最终能收敛。最终,智能体就能通过表格判断在某个状态下采取什么动作,才能获得最大的Q值。
Q-learning迭代计算:
Step1 给定学习参数γ和reward矩阵R
Step2 令Q=0
Step3 For each episode
步骤3中也可以细分:首先,可以随机选择一个初始状态s。然后当没有达到目标状态,则执行一下几步,在当前状态s的所有可能行为中选取一个行为a,再利用选定的行为a,得到下一个状态s1,按照前面规定的计算方式来计算Q(s, a),再把s1赋值给我们的s,进行下一步迭代计算。
这可能需要上千上万次才能收敛到一个状态。
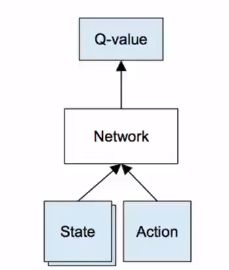
5.Deep Q Network
Q-table是Q学习算法中的一个关键概念,它是一个表格,记录了每个状态和动作对应的最大Q值。
Q-table中的每一行代表一个状态,每一列代表一个动作,表格中的每个元素Q(s,a)表示在状态s下采取动作a所能获得的最大收益的期望值。在Q-learning算法中,智能体通过不断探索环境,与环境交互,更新Q-table,从而逐渐学习到在特定状态下采取何种动作能够获得最大的收益.
-
Convert image to grayscale
-
Resize image to 80 * 80
-
Stack last 4 frames to produce an 80 * 80 * 4 input array for network
Exploration VS Exploitation : we both need.
δ - greedy exploration : have chances to explore.
6.DQN的环境搭建
我们主要是以小鸟为例子进行操作的。
import tensorflow as tf
import cv2
import sys
sys.path('game')
import random
import numpy as np
from collections import deque
GAME = 'bird'
# 或上或下
ACTIONs = 2
GAMMA = 0.99
OBSERVE = 1000
ECPLORE = 3000000
FINAL_EPSILOW = 0.0001
INITIAL = 0.1
REPLAY_MOMORY = 50000
RATCH = 32
FRAME_PER_ACTION = 1
def createNetwork():
# 三层卷积的形式
# 注意,池化层是没有参数的
W_conv1 = weights_variable([8, 8, 4, 32])
b_conv1 = bias_variable([32])
W_conv2 = weights_variable([4, 4, 32, 64])
b_conv2 = bias_variable([64])
W_conv3 = weights_variable([3, 3, 64, 64])
b_conv3 = bias_variable([32])
W_fc1 = weights_variable([1600,512])
b_fc1 = weights_variable([512])
W_fc1 = weights_variable([512,ACTIONS])
b_fc1 = weights_variable([ACTIONS])
s = tf.placeholder('float', [None,80,80,4])
h_conv1 = tf.nn.relu(conv2d(s,W_conv1,4)+b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
h_conv2 = tf.nn.relu(conv2d(h-pool1,W_conv2,2)+b_conv2)
# h_pool2 = max_pool_2x2(h_conv2)
h_conv3 = tf.nn.relu(conv2d(h-pool1,W_conv3,1)+b_conv3)
# reshape是将连接操作,将立体图转化为向量化数据
h_conv3_flat = tf.reshape(h_conv3, [-1,1600])
h_fc1 = tf.nn.relu(tf.matmul(h_conv3_flat,W_fc1)+b_fc1)
readout = tf.matmul(h_fc1,W_fc2) + b_fc2
return s,readout,h_fc1
def weights_variable(shape):
initial = tf.truncated_normal(shape,stddev=0.01)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.01,shape = shape)
return tf.Variable(initial)
def conv2d(x,W,stride):
return tf.nn.conv2d(x,W,strides=[1,stride,stride,1],padding='SAME')
def max_pool_2x2(x):
return nn.max_pool(x,ksize = [1,2,2,1],strides=[1,stride,stride,1],padding='SAME')
def trainNetwork(s,readout,,h_fc1,sess):
a = tf.placeholder('float', [None,ACTIONS])
y = tf.placeholder('float', [None])
readout_action = tf.reduce_mean(tf.multiply(readout,a),reduce_indices = 1)
cost = tf.reduce_mean(tf.square(y = readout_action))
train_step = tf.train.AdamOptimizer(1e-6).minimaize(cost)
game_state = game.GameState()
D = deque()
do_nothing = np.zeros(ACTIONS)
do_nothing[0] = 1
x_t,r_0,terminal = game_state.frame_step(do_nothing)
# 将图变为80*80的二维图像,在转化为1,255的
x_t = cv2.cvtColor(cv2.resize(x_t,(80,80),cv2.COLOR_BGR2CRAY))
ret,x_t = cv2.threshold(x_t,1,255,cv2.THRESH_BINARY)
s_t = np.stack((x_t,x_t,x_t,x_t),axis = 2)
saver = tf.train.Saver()
see.run(tf.initialize_all_variables())
checkpoint = tf.train.get_checkpoint_state('saved network')
if checkpoint and checkpoint.model_checkpoint_path:
saver.restore(sess, checkpoint.model_checkpoint_path)
print('Successfully loaded')
else:
print('load failed')
epsilon = INITIAL_EPSILOW
t = 0
while 'flappy bird' != 'angry bird':
readout_t = readout.eval(feed_dict = {s:[s_t]})[0]
a_t = np.zeros([ACTIONS])
action_index = 0
if t % 1 == 0:
if random.random() <= epsilon:
print('Rondom Action')
action_index = random.randint(ACTIONS)
a_t[action_index] = 1
else:
# 决定小鸟向上飞还是向下
action_index = np.argmax(readout_t)
a_t[action_index] = 1
x_t1_colored,r_t,r_t,terminal = game_state.frame_step(a_t)
x_t = cv2.cvtColor(cv2.resize(x_t1,colored,(80,80),cv2.COLOR_BGR2CRAY))
ret,x_t = cv2.threshold(x_t1,1,255,cv2.THRESH_BINARY)
x_t1 = np.reshape(x_t1, (80,80,1))
s_t1 = np.append(x_t1, s_t[:,:,3],axis = 2)
# 强化学习
D.append(s_t,a_t,r_t,s_t1,terminal)
# s_t当前状态
# a_t当前动作
# r_t奖励和回馈
# s_t1新的状态
# terminal判断是否结束
if len(D) > REPLAY_MOMORY:
D.popleft()
if t > OBSERVE:
minibatch = random.sample(D,BATCH)
s_j_batch = [d[0] for d in minibatch]
a_batch = [d[1] for d in minibatch]
r_batch = [d[2] for d in minibatch]
s_j1_batch = [d[3] for d in minibatch]
y_batch = []
# 神经网络的输出值
readout_j1_batch = readout.eval(feed_dict = [s:s_j1_batch])
for i in range(0, len(minibatch)):
terminal = minibatch[i][4]
if terminal:
y_batch.append(r_batch[i])
else:
y_batch.append(r_batch[i] + GAMMA*np.max(readout_j1_batch[i]))
train_step.run(feed_dict = {
y:y_batch,
a:a_batch,
s:s_j_batch,
})
# update information
s_t = s_t1
t += 1
if t % 10000 == 0:
saver.save(sess, './',global_step = t)
state = ''
if t <= OBSERVE:
state = 'OBSERVE'
else:
state = 'train'
print
def playGame():
sess = tf.InterativeSession()
s,readout,h_fel = createNetwork()
# 训练
trainNetwork()
def main():
playGame()
if __name__ == '__main__':
main()![]()