C++之单字符串匹配问题
有很多算法可以解决单模式匹配问题。而根据在文本中搜索模式串方式的不同,我们可以将单模式匹配算法分为以下几种:
- 基于前缀搜索方法:在搜索窗口内从前向后(沿着文本的正向)逐个读入文本字符,搜索窗口中文本和模式串的最长公共前缀。
- 著名的
Knuth-Morris-Pratt (KMP)算法和更快的Shift-Or算法使用的就是这种方法。
- 著名的
- 基于后缀搜索方法:在搜索窗口内从后向前(沿着文本的反向)逐个读入文本字符,搜索窗口中文本和模式串的最长公共后缀。使用这种搜索算法可以跳过一些文本字符,从而具有亚线性的平均时间复杂度。
- 最著名的
Boyer-Moore算法,以及Horspool算法、Sunday (Boyer-Moore 算法的简化)算法都使用了这种方法。
- 最著名的
- 基于子串搜索方法:在搜索窗口内从后向前(沿着文本的反向)逐个读入文本字符,搜索满足「既是窗口中文本的后缀,也是模式串的子串」的最长字符串。与后缀搜索方法一样,使用这种搜索方法也具有亚线性的平均时间复杂度。这种方法的主要缺点在于需要识别模式串的所有子串,这是一个非常复杂的问题。
Rabin-Karp算法、Backward Dawg Matching (BDM)算法、Backward Nondeterministtic Dawg Matching (BNDM)算法和Backward Oracle Matching (BOM)算法使用的就是这种思想。其中,Rabin-Karp算法使用了基于散列的子串搜索算法。
摘取自01.字符串基础知识 | 算法通关手册 (itcharge.cn)
这里主要是通过C++实现单模式串匹配问题
- Brute Force算法
- Rabin Karp算法
- KMP算法
- Boyer Moore算法
- Horspool算法
- Sunday算法
Brute Force算法
中文意思是暴力匹配算法,也可以叫做朴素匹配算法。
算法思想:将子串的第一个元素与主串的每一个元素逐一对比,直到在主串中匹配到该子串,或者找不到匹配子串。
代码实现如下:
int BruteForce(const string& t, const string& p) {
int i,j;
i = j = 0;
while (i < t.size() && j < p.size()) {
if (t[i] == p[j]) {
i += 1;
j += 1;
}
else {
//这波恢复属实精彩
i = i - (j - 1);
j = 0;
}
}
if (j == p.size()) return i - j;
else return -1;
}
代码较为简单,要注意的是,当匹配到n个元素,出现错误时,需要回到最开始匹配的地方。
时间复杂度分析:(n为主串长度,m为子串长度)
- 最好的情况:直接匹配成功,
O(m) - 最换的情况:每一次匹配都要进行
m次匹配,总共要进行n-m+1。 - 平均时间复杂度:在一般的情况下,根据等概率原则,时间复杂度
O(n+m)。
Rabin Karp算法
Rabin Karp算法简称为RK算法,
算法思想:对于给定文本串 T 与模式串 p,通过滚动哈希算法快速筛选出与模式串 p 不匹配的文本位置,然后在其余位置继续检查匹配项。
代码实例
int RabinKarp(const string& t, const string& p, int d,int q) {
if (t.size() < p.size()) return -1;
int hash_p, hash_t;
hash_p = hash_t = 0;
// 获取p和t的哈希值
for (int i = 0; i < p.size(); i++) {
hash_p = (hash_p * d + int(p[i]-'a')) % q;
hash_t = (hash_t * d + int(t[i]-'a')) % q;
}
// 最大一位为1的值
int power = int(pow(d,int(p.size()) - 1)) % q;
// 开始进行匹配
for (int i = 0; i < t.size() - p.size() + 1; i++) {
if (hash_p == hash_t) {
bool match = true;
for (int j = 0; j < p.size(); j++) {
if (t[i + j] != p[j]) {
match = false;
break;
}
}
if (match) return i;
}
if (i < t.size() - p.size()) {
hash_t = (hash_t - power * int(t[i]-'a')) % q; //减去前一个值
hash_t = (hash_t * d + int(t[i + p.size()]-'a')) % q; //加入新值
hash_t = (hash_t + q) % q; //确保 hash_t > 0
}
}
return -1;
}
对于这个RK算法,我们用到了4个参数,主串t,子串p,进制数d,以及最大取余数q。
RK算法主要用到了哈希函数,且采用的是进制hash函数。
比如 cat 的哈希值就可以表示为:
H a s h ( c a t ) = c × 26 × 26 + a × 26 + t × 1 = 2 × 26 × 26 + 0 × 26 + 19 × 1 = 1371 \begin{aligned} Hash(cat)&=c×26×26+a×26+t×1\\ &=2×26×26+0×26+19×1\\ &=1371 \end{aligned} Hash(cat)=c×26×26+a×26+t×1=2×26×26+0×26+19×1=1371
比如你的匹配字符串中有26个字符,那么可以采用26进制,这样就将cat通过哈希函数转换成了整数。不过为了防止数值过大而溢出,需要采用q对于计算的结果取余。
了解哈希函数之后,我们再来看代码。
- 防止p子串长度大于t主串。
- 计算p子串的哈希值,也计算和p相同长度的t截取部分的哈希值。
- 同时先储存p最高位且系数为1的值,方便后续计算。
- 然后遍历主串,从0到n-m+1,如果t的哈希值与p的哈希值相同,就进行后续的匹配操作,匹配成功则返回索引,失败了则继续循环。
- 如果上述匹配没有成功,那么就需要移动一步,并且重新计算t的哈希值,不过只需要去掉最高位,在重新计算就可以了。
可能有人会有疑惑,为什么哈希值相同了还需要进行匹配操作,那是因为哈希函数存在一个问题,那就是哈希冲突,即不同的子串却得到了相同的哈希值,因此最后还需要进行一步验证。
时间复杂度分析
如果不存在哈希冲突问题,那么时间复杂度为O(n),只需要遍历一次即可。
最坏的情况则是每次都会出现冲突,也就是BF算法一样,时间复杂度为O(m*n)
这里实现的RK算法,只针对小写字母,大写字符以及大小写混合,还需要修改提取ASCII值的那个部分。
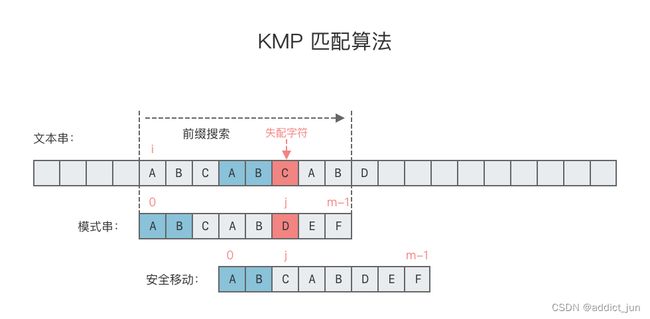
KMP算法
KMP 算法思想:对于给定文本串 T 与模式串 p,当发现文本串 T 的某个字符与模式串 p 不匹配的时候,可以利用匹配失败后的信息,尽量减少模式串与文本串的匹配次数,避免文本串位置的回退,以达到快速匹配的目的。
这里列举一个简单的例子
我们可以看到,KMP算法相比于BF算法,在匹配失败之后,KMP回退了2格,而BF算法要回退了4格,即起始位置的后一位。显然KMP算法的效率是更快的。那么他是怎么实现的呢?
它应用了额外的空间,即next数组。我们可以这样想,子串长度是3,那么无非就是4种情况,1.无匹配;2.匹配一个;3.匹配两个;4.匹配成功。
除掉最后第四种情况,我们只需要将上述三种情况发生,子串应该回退多少记录就行了。这样每次匹配失败,直接根据next数据进行回退就可以了。
当然next的构造肯定是需要通过代码实现的,而不是人为计算。
代码如下
vector<int> GenerateNext(const string& p) {
vector<int> next(p.size(), 0);
int left = 0;
for (int right = 1; right < p.size(); right++) {
while (left > 0 && p[left] != p[right]) left = next[left - 1]; //不同的,且left不为0的,等于left-1为索引的数组值。
if (p[left] == p[right]) left += 1; //遇到相同的,则left+1
next[right] = left; //next赋值
}
return next;
}
这里举一个例子ABCDEFG,他们都是不同的字符,所以都为0。
0 0 0 0 0 0 0
接下来我们再来看ABCABCF
0 0 0 1 2 3 0
这里next数组中的数字表示下一次匹配,可以跳过字符的个数。
当你匹配到第二个B,发现匹配错误,说明前4个字符匹配成功,然后查找最后一个匹配成功的next数组值,即A,值是1,代表下一次匹配可以跳过1个字符。
所以最后算法实现代码如下:
int Kmp(const string& t, const string& p) {
vector<int> next = GenerateNext(p);
int j = 0;
for (auto i = 0; i < t.size(); i++) {
while (j > 0 && t[i] != p[j]) j = next[j - 1]; //j-1表示最后一个匹配成功的字符
if (t[i] == p[j]) j++;
if (j == p.size()) return i-j+1;
}
return -1;
}
算法实现非常简单;
- 获取next数组
- 遍历主串
- 如果匹配失败,且j>0,则通过最后一次匹配成功的next数组值进行回退。
- 如果一个元素匹配成功,接着匹配下一个。
- 全部匹配成功,而返回匹配成功字符串的起始位置。
我们可以发现该算法速度极快,只需要O(n+m)。即next数组和一个for循环。
Boyer Moore算法
一种基于后缀的搜索匹配算法,如果想了解详细的原理,可以参考下面这篇文章,浅显易懂。
浅谈字符串匹配算法 —— BM算法_-红桃K的博客-CSDN博客_bm算法的优缺点
如果阅读了上述博客之后,这里我们在进行字符串匹配的代码实现。
首先是坏字符表
unordered_map<char, int> GenerateBadCharTable(const string& p) {
unordered_map<char, int> bc_table;
for (auto i = 0; i < p.size(); i++) bc_table[p[i]] = i;
return bc_table;
}
这里将出现过的字符进行一对一赋值,我们可以发现最后相同字符对应的值为该字符最后一次出现的位置。坏规则表有什么作用呢?
-
如果匹配到坏字符,发现坏字符不在字典中,则直接大步移动子串到新一位。
-
如果匹配到坏字符在字典中,可能出现两种情况,这里讲一下位移为负的情况
a b c c c
c e c
这里我们匹配到c和e是不同的,然后我们查到坏字符表总的c的值为2(取字符最后一次出现)这样我们计算移动位置,1-2=-1,反而要想向后移动,这样是不合理的,所以就需要另一个规则,好后缀。
这里时间复杂度为O(m)
接下来是好后缀
vector<int> GenerageSuffixArray(const string& p) {
vector<int> suffix(p.size(), 0);
for(int i = p.size() - 2; i >= 0; i--) {
int start = i;
while (start >= 0 && p[start] == p[p.size() - 1 - i + start]) start--;
suffix[i] = i - start; // 更新下标以i结尾的子串与模式后缀匹配的最大长度
}
return suffix;
}
这里需要先构建suffix数组,其中 suffix[i] = s 表示为以下标 i 为结尾的子串与模式串后缀匹配的最大长度为 s。即满足 p[i-s...i] == p[m-1-s, m-1] 的最大长度为 s。
这个数组里面每一个结尾的子串都是和后缀进行比较,所以称为好后缀。
加下来就是生成好后缀后移位数表gs_list代码如下:
这里好后缀规则后移位数表有三种情况
- 模式串中有子串匹配上好后缀。
- 模式串中无子串匹配上好后缀,但有最长前缀匹配好后缀的后缀。
- 模式串中无子串匹配上好后缀,也找不到前缀匹配。
vector<int> GenerageGoodSuffixList(const string& p) {
vector<int> gs_list(p.size(), p.size()); //初始化时,假设全部为情况3
vector<int> suffix = GenerageSuffixArray(p);
int j = 0; // j为好后缀前的坏字符位置
for (int i = p.size() - 1; i >= 0; i--) { // 情况2 从最长的前缀开始检索
if (suffix[i] == i + 1) { // 匹配到前缀, p[0...i]==p[m-1-i...m-1]
while(j < p.size()-1-i){
if (gs_list[j] == p.size()) {
gs_list[j] = p.size() - 1 - i; //更新在j处遇到坏字符可向后移动位数
}
j++;
}
}
}
//情况1 匹配到子串 p[i-s...i] == p[m-1-s, m-1]
for (int i = 0; i < p.size() - 1; i++) {
gs_list[p.size() - 1 - suffix[i]] = p.size() - 1 - i;
}
return gs_list;
}
这里全程是取后缀进行比较,不必考虑前缀或者内部子串与内部子串是匹配的。这个位移表核心的作用就是如果在第j位出现错误匹配,那么后面的好后缀是否在子串p后面存在相同的匹配,存在则位移到前方。
根据三种情况,如果好后缀匹配不到,则直接赋为最大值。
如果匹配得到,则位移到匹配的地方。这里通过先分析前缀,在分析内部子串来进行全覆盖分析。
- 前缀的话,计算j在任意匹配位置上出现换字符的移动位数
- 内部字串的话,直接更新匹配到字符的位置即可。
BM算法时间复杂度分析
- BM 算法在预处理阶段的时间复杂度为 O(n+σ),其中 σ 是字符集的大小。
- BM 算法在搜索阶段最好情况是每次匹配时,模式串
p中不存在与文本串T中第一个匹配的字符。这时的时间复杂度为 O(n/m)。 - BM 算法在搜索阶段最差情况是文本串
T中有多个重复的字符,并且模式串p中有m - 1个相同字符前加一个不同的字符组成。这时的时间复杂度为 O(m∗n)。 - 当模式串
p是非周期性的,在最坏情况下,BM 算法最多需要进行 3∗n 次字符比较操作。
Horspool算法
「Horspool 算法」 是一种在字符串中查找子串的算法,它是由 Nigel Horspool 教授于 1980 年出版的,是首个对 Boyer Moore 算法进行简化的算法。
代码实现
unordered_map<char, int> GenerateBadCharTable_2(const string& p) {
unordered_map<char, int> bc_table;
for (auto i = 0; i < p.size()-1; i++) bc_table[p[i]] = p.size()-1-i; //更新遇到坏字符可向右移动的距离
return bc_table;
}
和BM不一样的是,这个坏字符表的数值和BM是相反的,BM是递增,Horspool是递减。相同之处则是,如果遇到相同字符,以最右侧的字符的值为准。
代码实现
int Horspool(const string& t, const string& p) {
int n = t.size();
int m = p.size();
unordered_map<char, int> bc_table = GenerateBadCharTable_2(p);
int i = 0;
while (i <= n - m) {
int j = m - 1;
while (j > -1 && t[i + j] == p[j]) j -= 1; //进行后缀匹配
if (j < 0) return i;
//失败则通过坏字符表进行移位
i += bc_table.find(t[i + m - 1]) != bc_table.end() ? bc_table[t[i + m - 1]] : m;
}
return -1;
}
这次的实现则只有坏字符表,因为这里的坏字符采用的是逐渐递减的移位方式,如果匹配失败,则对比后缀最后一位数字,来进行移位操作。
- Horspool 算法在平均情况下的时间复杂度为 O(n),但是在最坏情况下时间复杂度会退化为 O(n∗m)。
Sunday算法
Sunday 算法思想:对于给定文本串 T 与模式串 p,先对模式串 p 进行预处理。然后在匹配的过程中,当发现文本串 T 的某个字符与模式串 p 不匹配的时候,根据启发策略,能够尽可能的跳过一些无法匹配的情况,将模式串多向后滑动几位。
与Horspool不同的是,如果匹配失败,它关注的是参加匹配的末尾字符的下一位字符。
首先是坏字符表
unordered_map<char, int> GenerateBadCharTable_3(const string& p) {
unordered_map<char, int> bc_table;
for (auto i = 0; i < p.size(); i++) bc_table[p[i]] = p.size() - i; //更新遇到坏字符可向右移动的距离
return bc_table;
}
对于坏字符表和Horspool算法不一样的是,这里少了一个-1。且覆盖到所有元素
然后是代码实现
int Sunday(const string& t, const string& p) {
int n = t.size();
int m = p.size();
unordered_map<char, int> bc_table = GenerateBadCharTable_3(p);
int i = 0;
while (i <= n - m) {
int j = 0;
if (t.substr(i, m) == p) return i; //匹配完成,返回模式串p
if (i + m >= n) return -1;
i += bc_table.find(t[i + m]) != bc_table.end() ? bc_table[t[i + m]] : m+1;
}
return -1;
}
首先进行完成的匹配,如果匹配成功,则返回i。如果偏移量i加上子串m的长度大于n,推出,匹配失败。
然后就是位移准则:匹配失败之后,直接匹配主串中匹配失败末尾的后一位字符,进行移位操作。
算法的时间分析
- Sunday 算法在平均情况下的时间复杂度为 O(n),但是在最坏情况下时间复杂度会退化为 O(n∗m)。
总结:
BM算法非常的复杂,而且也会有效率不高的情况,但是它常态的效率却是KMP的2~3倍,而KMP的效率可以说是非常快了,所以说BM还是非常经典的算法。
每次对同一个问题,不同的解决办法时,我们总需要思考和总结他们对这个问题的优化思路是什么?
- 牺牲一定的效率,提高代码的健壮性和稳定性。
- 面对某个多次调动的表达式,通过预处理,或者缓存来实现加速。
- 通过空间来换时间。
- 又或者对于查找,采用hash结构来提高效率。
等等,都是值得我们思考和总结的。
如果有用希望得到大家的二连,同时也感觉大家的阅读。