《剑指offer》 -day4-查找算法（简单）--【二分专题】

剑指 Offer 03. 数组中重复的数字

题目描述

找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

限制：

• $2<=n<=100000$

排序

思路：

• 对nums中所有元素排序
• 从前向后扫描，遇到相邻元素相同，则为重复元素

class Solution {
    public int findRepeatNumber(int[] nums) {
        Arrays.sort(nums); // 排序
        for (int i = 1; i < nums.length; i++) {
        	// 相邻元素相同，则为重复元素
            if (nums[i] == nums[i - 1]) return nums[i];
        }
        return -1; // 不存在重复的数字
    }
}

• 时间复杂度：$O(nlogn)$ （快排）
• 空间复杂度：$O(logn)$ （快排 的栈消耗）
  

哈希

Map

思路：使用Map统计nums中每个元素的个数，取 次数大于1的，即可。

简单，但是带来很多不必要的统计，而且 Map 消耗空间较大

class Solution {
    public int findRepeatNumber(int[] nums) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int i : nums) {
            map.put(i, map.getOrDefault(i, 0) + 1);
        }
        for (int i : map.keySet()) {
            if (map.get(i) > 1) {
                return i;
            }
        }
        return -1; // 没有重复的数
    }
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$
  

Set

本题是只用找到一个重复的数字，即可。所以，使用 Set 比 Map 更友好一些。但是，如果要找所有重复的数字 以及 次数，那还是得用 Map。

思路：

• 使用 Set 一次 for，每次查看当前元素 i 是否在 set中
• 若 i 在 set 中，则说明 i 为重复元素；
• 否则，则将 i 添加到 set 中

Note：二者顺序 不可颠倒…

class Solution {
    public int findRepeatNumber(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for (int i : nums) {
            if (set.contains(i)) return i; // ！！！ 二者顺序 不可颠倒...
            set.add(i);
        }
        return -1; // 没有重复的数
    }
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

数组

• 题目中说了所有元素都在 $[0,n-1]$ 内，所以可以使用一个长度为 $n$ 的数组来作为哈希表，即可。

class Solution {
    public int findRepeatNumber(int[] nums) {
        int n = nums.length;
        int[] hash = new int[n];
        for (int i : nums) {
            if (hash[i] > 0) {
                return i;
            }
            hash[i]++;
        }
        return -1; // 无
    }
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

重排 ⭐️

• 原地算法，参考 题解

题目说了：所有数字都在 0～n-1 的范围内。如果这个数组中没有重复数字，则数组排序后数字 i 应该出现在下标 i 的位置；否则，有些可能存在多个数字，同时有些位置没有数字。

思路：

• 从头到尾扫描数组
• 若 nums[i] == i（元素和下标 能对上，即 萝卜在它的坑），则 继续向后扫描；
• 若 nums[i] != i（元素和下标 对不上，即 萝卜不在它的坑），则 需要将 nums[i] 和第 nums[i] 个元素（即，nums[nums[i]]）进行比较：
  • 如果二者相等，即 nums[i] == nums[nums[i]]，则说明找到重复元素（两个萝卜一个坑）
  • 否则，则 交换二者（即，将萝卜放到它应该的坑里）

栗子：
以 $nums=2,3,1,0,2,4,,3$ 为例，初始化 i = 0。

• 由于 $nums[0]=2!=0$ 并且 $nums[2]=1!=2$，所以交换二者，得到 $nums=1,3,2,0,2,4,,3$
• 此时 $nums[0]=1!=0$ 并且 $nums[1]=3!=1$，所以交换二者，得到 $nums=3,1,2,0,2,4,,3$
• 仍然 $nums[0]=3!=0$ 并且 $nums[3]=0!=3$，所以交换二者，得到 $nums=0,1,2,3,2,4,,3$
• 此时 $nums[0]=0==0$（萝卜放入正确的坑了），继续向后扫描，即 i = 1
• 可以看到 i = 1、2、3 时，均为 $nums[i]==i$，继续向后扫描即可，即 i = 4
• 此时 $nums[4]=2!=4$ 并且 $nums[2]=2==3$，所以得到 重复元素 2

class Solution {
    public int findRepeatNumber(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            // 若当前位置元素和下标不相等，则交换之（相当于把萝卜放到正确的坑中）
            while (nums[i] != i) {
            	// 交换前查看一下，若当前元素和要交换的元素相等（两个萝卜一个坑），则说明遇到重复元素。 
                if (nums[i] == nums[nums[i]]) return nums[i];
                swap(nums, i, nums[i]);
            }
        }
        return -1; // 不存在重复的数字
    }

    public void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

剑指 Offer 53 - I. 在排序数组中查找数字 I

题目描述

统计一个数字在排序数组中出现的次数。

提示：

• $0<=nums.length<=10^5$
• $10^9<=nums[i]<=10^9$
• nums 是一个非递减数组
• $-10^9<=target<=10^9$

暴力

思路：纯暴力，一个一个找

class Solution {
    public int search(int[] nums, int target) {
        int res = 0;
        for (int i = 0; i < nums.length; i++){
            if (nums[i] == target) {
                res++;
            }
        }
        return res;
    }
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

二分查找 （一次二分）

有序数组，一般可以联想到使用二分求解

思路：

• 题目说了 该数组 nums 已经是 排序数组，所以可以使用 二分查找。
• 先用二分查找在 nums 中查找 target，并返回下标 index：
• 若 index == -1，说明 nums 中没有 target，则直接 return 0 即可；
• 若 index != 1，则需要从 i = index 开始 向左、向右 查找 nums 中元素值为 target 的左右边界 [left, right]。则最终 target 次数为 $right-left+1$。

class Solution {
    public int search(int[] nums, int target) {
        int res = 0;
        // 二分查找，找到一个为target的下标
        int index = binarySearch(nums, target);
        if (index == -1) { // 不存在 target
            return 0;
        }
        System.out.println("index = " + index);
        // 向前滑动
        int left = index; // target 左端点
        while (left > 0 && nums[left] == nums[left - 1]) {
            left--;
        }
        System.out.println("left = " + left);
        // 向后滑动
        int right = index; // target 右端点
        while (right + 1 < nums.length && nums[right] == nums[right + 1]) {
            right++;
        }
        return right - left + 1;
    }

    int binarySearch(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1; // 左闭右闭区间 [left, right]
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                return mid;
            }
        }
        return -1; // 不存在
    }
}

• 时间复杂度：最好 $O(logn)$（target不太多）、最差 $O(n)$（nums中几乎全是 target，左右滑动找 left、right 时间为 $O(n)$）
• 空间复杂度：$O(1)$

二分查找 （2次二分）⭐️

参考 K佬题解

上面一次 二分查找 的最坏时间复杂度为 $O(n)$，所以可以 通过 2次 二分查找：分别找 $nums[i]==target$ 的 left 和 right。

思路：

1. 先通过第一次二分，搜索右边界 right（nums中最右的target 右边第一个元素下标）；
2. 然后，再通过第二次二分 ，搜索左边界 left（nums中最左的target 左边第一个元素下标）；
3. 最终，$nums$ 中值为 $target$ 的元素个数为 right - left - 1

class Solution {
    public int search(int[] nums, int target) {
        if (nums.length == 0) return 0;
        // 搜索右边界（nums中最右的target 右边第一个元素下标）
        int i = 0;
        int j = nums.length - 1; // 左闭右闭区间
        while (i <= j) {
            int mid = i + (j - i) / 2;
            if (nums[mid] <= target) { // 相等，说明右边界（最右的target右边第一个元素下标）一定在mid右边
                i = mid + 1;
            } else {
                j = mid - 1;
            }
        }
        int right = i; // 右边界为退出时候的i
        System.out.println("right = " + right);
        // 搜索左边界（nums中最左的target 左边第一个元素下标）
        i = 0;
        j = nums.length - 1;
        while (i <= j) {
            int mid = i + (j - i) / 2;
            if (nums[mid] < target) {
                i = mid + 1;
            } else { // // 相等，说明左边界（最左的target左边第一个元素下标）一定在mid左边
                j = mid - 1;
            }
        }
        int left = j;
        System.out.println("left = " + left);
        return right - left - 1;
    }
}

• 时间复杂度：$O(logn)$
• 空间复杂度：$O(1)$

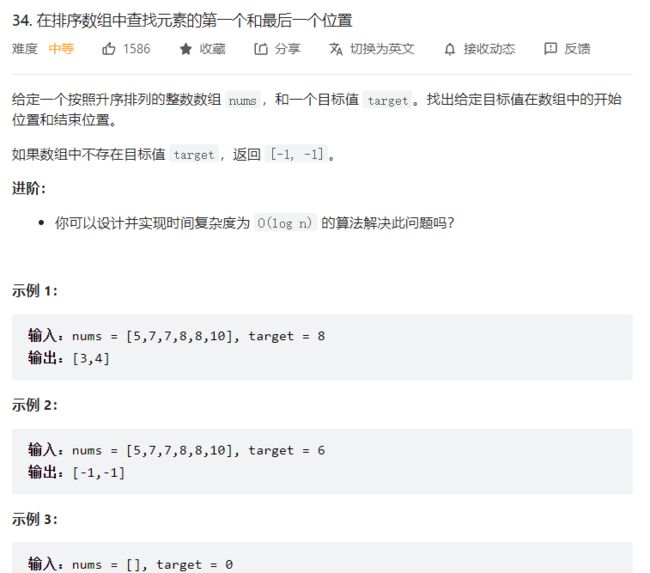
34. 在排序数组中查找元素的第一个和最后一个位置

提示：

• 0 <= nums.length <= 10^5$
• $-10^9<=nums[i]<=10^9$
• nums 是一个非递减数组
• $-10^9<=target<=10^9$

本题中数组也是有序的，所以也可以采用 “两次二分查找”，分别查找 左边界、右边界

class Solution {
    public int[] searchRange(int[] nums, int target) {
        if (nums.length == 0) {
            return new int[] {-1, -1};
        } 
        int i = 0;
        int j = nums.length - 1;
        // 找target右边界
        while (i <= j) {
            int mid = i + (j - i) / 2;
            if (nums[mid] <= target) { // 相等，说明右边界在mid右边
                i = mid + 1;
            } else {
                j = mid - 1;
            }
        }
        int right = j;
        System.out.println("right = " + right);
        // nums中不存在target
        if (right == -1 || nums[right] != target) {
            return new int[] {-1, -1};
        }
        // 找target左边界
        i = 0;
        j = nums.length - 1;
        while (i <= j) {
            int mid = i + (j - i) / 2;
            if (nums[mid] < target) {
                i = mid + 1;
            } else { // 相等，说明左边界在mid左边
                j = mid - 1;
            }
        }
        int left = i;
        System.out.println("left = " + left);
        System.out.println("right = " + right);
        return new int[] {left, right};
    }
}

• 时间复杂度：$O(logn)$
• 空间复杂度：$O(1)$
  

剑指 Offer 53 - II. 0～n-1中缺失的数字

题目描述

一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

限制：

• $1<=数组长度<=10000$

排序

思路：

• 题目中说了 所有元素都在$0～n-1$内、元素唯一、且缺少一个元素，所以，可以利用题目信息
• 首先，对 $nums$ 升序排序；
• 然后，遍历 $nums$，若 “当前下标$i$ 和 元素$nums[i]$不相等，则说明找到缺失元素”，返回下标 $i$；
• 最终，退出 for 时，说明“缺失元素为 $n$”，返回“数组长度$n$即可”

class Solution {
    public int missingNumber(int[] nums) {
        Arrays.sort(nums);
        for (int i = 0; i < nums.length; i++) {
            if (i != nums[i]) return i;
        }
        return nums.length; // 数组中没有n
    }
}

• 时间复杂度：$O(nlogn)$ （快排时间消耗）
• 空间复杂度：$O(1)$ （忽略快排栈的空间消耗）
  

哈希-数组

思路：使用哈希表（范围不大，这里用数组就 ok）标记 $nums$ 每个元素出现的情况，最后再一遍扫描 arr 中为 0 的即为 缺失元素。

class Solution {
    public int missingNumber(int[] nums) {
        int[] arr = new int[nums.length + 1]; // 这里是 n + 1，而不是 n
        for (int i = 0; i < nums.length; i++) {
            arr[nums[i]]++;
        }
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == 0) {
                return i;
            }
        }
        return -1; // 无
    }
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$
  

二分查找 ⭐️

参考 K佬题解

Note：题目中说了 给定的数组为 排序数组，有序数组常会用到 二分法 或 双指针。

本题采用 二分法 是一种更优的解法…

思路：

• 给定数组有序，所以可以考虑用 二分
• 将数组分为 2 个部分：
  • 左子数组， 即 $nums[i]==i$；–> 左边部分
  • 右子数组， 即 $nums[i]!=i$；–> 右边部分
• 则缺失的数字为 右子数组的第一个元素对应的下标

class Solution {
    public int missingNumber(int[] nums) {
        int left = 0;
        int right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == mid) { // 仍然在左子数组中，缺失数字（即 右子数组的第一元素对应下标）在 [mid + 1, len - 1] 中
                left = mid + 1;
            } else { // 在右子数组中了，但是需要找右子数组的第一个元素，缺失数字在 [left, mid - 1] 中
                right = mid - 1;
            }
        }
        return left; // 右子数组 第一个元素对应的下标
    }
}

• 时间复杂度：$O(logn)$
• 空间复杂度：$O(1)$