《剑指offer》 -day5-查找算法（中等）【二分】

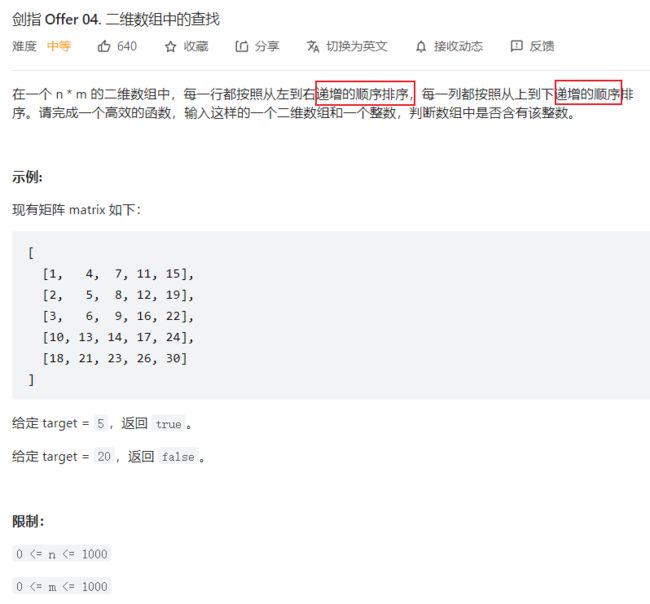
剑指 Offer 04. 二维数组中的查找

暴力

思路：一个一个找，效率低。

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        if (matrix.length == 0) return false;
        int n = matrix.length;
        int m = matrix[0].length;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (matrix[i][j] == target) {
                    return true;
                }
            }
        }
        return false;
    }
}

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

二分

思路：

• 因为数组 $matrix$ 中的 行、列 均有序，所以可以考虑使用 二分查找。

逐行二分

思路

• 若 matrix[i][0] <= target，则逐行二分查找 $target$；
• 否则，说明当前 $matrix$ 中不存在 $targetr$.

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        if (matrix.length == 0 || matrix[0].length == 0) return false;
        int n = matrix.length;
        int m = matrix[0].length;
        // 对所有行，逐行进行二分
        for (int i = 0; i < n && matrix[i][0] <= target; i++) {
            int left = 0;
            int right = m - 1; // 左闭右闭
            while (left <= right) {
                int mid = left + (right - left) / 2;
                if (matrix[i][mid] < target) {
                    left = mid + 1;
                } else if (matrix[i][mid] > target) {
                    right = mid - 1;
                } else {
                    return true;
                }
            }
        }
        return false; // 不存在
    }
}

• 时间复杂度：$O(nlogn)$ （逐行二分）
• 空间复杂度：$O(1)$

两次二分

注意：无法利用“二段性” 直接定位 $target$ “可能” 所在的行 row（定位到的 row 只是 $>target$ 和 $<target$ 的 “行分界”）

但是，可以首先通过“二分”找到 row，然后从 row 开始逆序 逐行二分。

思路

1. 第一次二分：查找 row

   利用“二段性”，所以定位到的 row 只是 $>target$ 和 $<target$ 的 “行分界”

2. 从 row 开始 逆序逐行二分：在matrix[i]中查找target

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        if (matrix.length == 0 || matrix[0].length == 0) return false;
        int n = matrix.length;
        int m = matrix[0].length;
        // 1、第一次二分：查找row
        int left = 0;
        int right = n - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (matrix[mid][0] < target) {
                left = mid + 1;
            } else if (matrix[mid][0] > target) {
                right = mid - 1;
            } else {
                return true;
            }
        }
        int row = right; // target“可能”存在的行
        System.out.println("row = " + row);
        // 2、从row开始 逆序逐行二分：在matrix[i]中查找target
        for (int i = row; i >= 0; i--) {
            left = 0;
            right = m - 1;
            while (left <= right) {
                int mid = left + (right - left) / 2;
                if (matrix[i][mid] < target) {
                    left = mid + 1;
                } else if (matrix[i][mid] > target) {
                    right = mid - 1;
                } else {
                    return true;
                }
            }
        }
        return false; // 不存在
    }
}

• 时间复杂度
  • 最坏 $O(nlogn)$（row在中间一行，但是$target$在第一行，此时需要对 $n/2$行 进行二分）
  • 最好 $O(logn\ast logn)$ （row直接定位到了 $taraget$ 所在行，只用进行对一行进行 二分）
• 空间复杂度：$O(1)$
  

二分查找树 ⭐️

思路

• 题目中说了 每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。所以，可以把整个 $matrix$ 看成一颗以 右上角（即，(0, m)）为 root 的 BST.
• 初始化：i = 0; j = m - 1;
• 若 $matrix[i][j]>target$，表示 target “可能” 在 左子树中，所以 j--;
• 若 $matrix[i][j]<target$，表示 target “可能” 在 右子树中，所以 i++;

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        if (matrix.length == 0) { // 空矩阵，单独处理
            return false;
        }
        int n = matrix.length;
        int m = matrix[0].length;
        // 以右上角为 root，看成一颗 BST
        int i = 0;
        int j = m - 1;
        while (i < n && j >= 0) {
            if (matrix[i][j] > target) { // 左子树
                j--;
            } else if (matrix[i][j] < target) { // 右子树
                i++;
            } else {
                return true;
            }
        }
        return false;
    }
}

• 时间复杂度：$O(n+m)$
• 空间复杂度：$O(1)$
  

剑指 Offer 11. 旋转数组的最小数字

提示：

• $n==numbers.length$
• $1<=n<=5000$
• $-5000<=numbers[i]<=5000$
• numbers 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

注意：本题与主站 154 题相同：https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array-ii/

暴力

class Solution {
    public int minArray(int[] numbers) {
        int res = Integer.MAX_VALUE;
        int n = numbers.length;
        for (int i : numbers) {
            res = res < i ? res : i;
        }
        return res;
    }
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$
  

二分 ⭐️

和 二分专题 中的 81. 搜索旋转排序数组 II 类似，但较之更为简单一些。

思路

• 由于本题中 $nums$ 可能存在重复元素，所有首先需要“维护两段性”之后才能使用 二分；

  参考： 二分专题 中的 81. 搜索旋转排序数组 II

• 使用 二分查找“旋转点” index
  • 若 $nums$ 整体升序（即，“旋转点”为$n$），此时 min为 $number[0]$；
  • 否则，即 $index<n$ 时，则“旋转点” numbers[index] 即为 最小值 min。

class Solution {
    public int minArray(int[] numbers) {
        int n = numbers.length;
        int left = 0;
        int right = n - 1;
        // 维护“两段性”（数组只有一个元素时，不用维护，所以是 `<`）
        while (left < right && numbers[right] == numbers[0]) { 
            right--;
        }
        System.out.println("right1 = " + right);
        // 二分：找“旋转点”
        while (left <= right) { // 左闭右闭（这里是 <=）
            int mid = left + (right - left) / 2;
            if (numbers[mid] >= numbers[0]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        int index = left; // 旋转点
        System.out.println("left = " + left);
        System.out.println("right = " + right);
        // 若nums整体升序（即，没有旋转、或称之为“旋转点”为n），此时min为number[0]
        return index >= n ? numbers[0] : numbers[index];
    }
}

• 时间复杂度：$O(logn)$
• 空间复杂度：$O(1)$
  

类似题目

• 153. 寻找旋转排序数组中的最小值
• 154. 寻找旋转排序数组中的最小值 II

剑指 Offer 50. 第一个只出现一次的字符

暴力 + HassMap

思路：

• 使用 Map 统计 s 中每个字符出现的次数；
• 再次对 s 从前向后扫描，找到第一次只出现一次的 字符。

class Solution {
    public char firstUniqChar(String s) {
        Map<Character, Integer> map = new HashMap<>();
        for (char c : s.toCharArray()) {
            map.put(c, map.getOrDefault(c, 0) + 1);
        }
        for (char c : s.toCharArray()) {
            if (map.get(c) == 1) {
                return c;
            }
        }
        return ' '; // 不存在
    }
}

本题使用 HashMap 是更好的选择，当然 直接用 Set 其实也是可以的。

• 时间复杂度：$O(n\ast 2)$ （在忽略Map存、取时间消耗的前提下）
• 空间复杂度：$O(n)$

LinkedHashMap 有序 ⭐️

参考：K佬题解

思路：

• 由于 HashMap 无序，所以需要遍历两遍 s；
• 而 LinkedHashMap 是有序的（可以保证 FIFO），可以只遍历一遍 s、再遍历一遍 LinkedHashMap即可（map 中至多不超过 $26$ 个元素）

class Solution {
    public char firstUniqChar(String s) {
        HashMap<Character, Boolean> map = new LinkedHashMap<>();
        char[] arr = s.toCharArray();
        // 1、遍历s
        for (char c : arr) {
            map.put(c, !map.containsKey(c)); // 巧妙！
        }
        // 2、遍历map（最多不超过26）
        for (Map.Entry<Character, Boolean> entry : map.entrySet()) {
            if (entry.getValue()) {
                return entry.getKey();
            }
        }
        return ' '; // 不存在
    }
}

• 时间复杂度：$O(n\ast 1)$
• 空间复杂度：$O(n)$