常见图像噪声和常见图像噪声处理算法

1、图像噪声

1.1图像噪声的分类

图像噪声按噪声与信号的关系可分为加性噪声和乘性噪声；按照产生原因可分为外部噪声和内部噪声；按照统计特性可分为平稳噪声和非平稳噪声；平稳噪声基于统计后的概率密度函数又可以分为：高斯噪声、泊松噪声、脉冲噪声、瑞利噪声。

1.2基于统计后的概率密度函数

图像噪声的种类是根据不同分类方法而划分的，硬件工程师为了排查故障，可能更为关注外部噪声和内部噪声；通信工程师可能会分为加性噪声和乘性噪声；为了对图像进行去噪，图像处理工程师更多的关注其统计后的概率密度，从而建立数学模型去处理相应的噪声

1.2.1高斯噪声

 高斯噪声污染图

高斯噪声的产生原因主要是图像在拍摄时不够明亮、亮度不够均匀；电路各元器件自身噪声和相互影响；传感器长期工作温度过高等。

1.2.2椒盐噪声

椒盐噪声是脉冲噪声取值0或1的特例。它是一种随机出现的黑点（胡椒）或者白点（盐），前者是高灰度噪声，后者是低灰度噪声，一般两者同时出现在图像中。如下图所示：

一般低光照条件下，图像的噪声多为椒盐噪声而不是高斯噪声，比如矿井下的图像。椒盐噪声通常使用中值滤波器进行处理。

2、图像去噪算法

2.1空域滤波

空域滤波是在原图像上直接进行数据运行，对像素值进行处理。如邻域平均法、中值滤波、低通滤波等。

2.1.1均值滤波

在进行均值滤波时，首先要考虑需要对周围多少个像素点取平均值。通常情况下，我们会以当前像素点为中心，对行数和列数相等的一块区域内的所有像素点的像素值求平均。

例：

对于矩阵：

对所选定的3×3矩阵，选定中心像素点，对这个矩阵进行运算

中心点新值 = （ 1 +8 + 15 + 2 + 9 + 16 + 3 + 10 + 17）/9

                   = 9

对于边缘像素点，如图所示：

新值 = （ 1 + 8 + 2 + 9）/4

           =  5

除此以外，还可以扩展当前图像的周围像素点。完成图像边缘扩展后，可以在新增的行列内填充不同的像素值。OpenCV提供了多种边界处理方 式，我们可以根据实际需要选用不同的边界处理模式。

2.1.1.1OpenCv实现均值滤波

在OpenCV中，实现均值滤波的函数是cv2.blur（），其语法格式为：          

        dst=cv2.blur（src,ksize,anchor,borderType）

        式中：

         ● dst是返回值，表示进行均值滤波后得到的处理结果。

         ● src 是需要处理的图像，即原始图像。它可以有任意数量的通道，并能对各个通道独立处理。图像深度应该是CV_8U、CV_16U、CV_16S、CV_32F 或者 CV_64F中的一种。

        ● ksize是滤波核的大小。滤波核大小是指在均值处理过程中，其邻域图像的高度和宽度。

        ● anchor 是锚点，其默认值是（-1,-1），表示当前计算均值的点位于核的中心点位置。该值使用默认值即可，在特殊情况下可以指定不同的点作为锚点。

        ● borderType是边界样式，该值决定了以何种方式处理边界。一般情况下不需要考虑该值的取值，直接采用默认值即可。                      

            通常情况下，使用均值滤波函数时，对于锚点anchor和边界样式borderType，直接采用其默认值即可。因此，函数cv2.blur（）的一般形式为：

        dst=cv2.blur（src,ksize）    

2.1.1.2程序实例   

import cv2  as cv
import numpy as np
 
def cv_show(name, img):
    cv.imshow(name, img)
    cv.waitKey(0)
    cv.destroyAllWindows()
 
# 在图片上生成椒盐噪声
def add_peppersalt_noise(image, n=10000):
    result = image.copy()
    # 测量图片的长和宽
    w, h =image.shape[:2]
    # 生成n个椒盐噪声
    for i in range(n):
        x = np.random.randint(1, w)
        y=  np.random.randint(1, h)
        if np.random.randint(0, 2) == 0 :
            result[x, y] = 0
        else:
            result[x,y] = 255
    return result
 
# 在图片上生成高斯噪声
def add_gauss_noise(image, mean=0, val=0.01):
    size = image.shape
    image = image / 255
    gauss = np.random.normal(mean, val**0.05, size)
    image = image + gauss
    return image
 
# blur均值滤波，对高斯噪声有较好的去除效果，对象可以是彩色图像和灰度图像
img = cv.imread('D:\\dlam.jpg')
if img is None:
    print('Failed to read the image')
 
img1 = add_peppersalt_noise(img)
cv_show('img', img1)
 
# 默认为规定尺寸的1/n的全1矩阵
img2 = cv.blur(img1, (3, 3))
cv_show('img2', img2)
 
img3 = cv.blur(img1, (5, 5))
cv_show('img3', img3)
 
# 观察不同滤波核对图像滤波的影响

例：

原图

添加椒盐噪声后

3X3卷积核滤波结果

 5X5卷积核滤波结果

 2.1.2高斯滤波

 在进行均值滤波时，其邻域内每个像素的权重是相等的。在高斯滤波中，会将中心点的权重值加大，远离中心点的权重值减小，在此基础上计算邻域内各个像素值不同权重的和。

2.1.2.1OpenCv实现均值滤波

在OpenCV中，实现中值滤波的函数是cv2.medianBlur（），其语法格式如下：

         dst=cv2.medianBlur（src,ksize）

        式中：

        ● dst是返回值，表示进行中值滤波后得到的处理结果。

         ● src 是需要处理的图像，即源图像。它能够有任意数量的通道，并能对各个通道独立处理。图像深度应该是CV_8U、CV_16U、CV_16S、CV_32F 或者 CV_64F中的一种。

        ● ksize 是滤波核的大小。滤波核大小是指在滤波处理过程中其邻域图像的高度和宽度。需要注意，核大小必须是比1大的奇数，比如3、5、7等。 

2.1.2.2程序实例

import cv2  as cv
 
def cv_show(name, img):
    cv.imshow(name, img)
    cv.waitKey(0)
    cv.destroyAllWindows()
 
 
def add_peppersalt_noise(image, n=10000):
    result = image.copy()
    # 测量图片的长和宽
    w, h =image.shape[:2]
    # 生成n个椒盐噪声
    for i in range(n):
        x = np.random.randint(1, w)
        y=  np.random.randint(1, h)
        if np.random.randint(0, 2) == 0 :
            result[x, y] = 0
        else:
            result[x,y] = 255
    return result
 
 
img = cv.imread('D:\\dlam.jpg')
if img is None:
    print('Failed to read the image')
 
img1 = add_peppersalt_noise(img)
cv_show('after', img1)
 
# 中值滤波，可对灰色图像和彩色图像使用
img2 = cv.medianBlur(img1, 3)
cv_show('after1', img2)
# ksize变大图像变模糊
img3 = cv.medianBlur(img1, 9)
cv_show('after2', img3)

原图如下：

        

添加高斯噪声：

 高斯滤波结果：

        高斯滤波对高斯噪声消除效果较好。

2.1.3中值滤波

之前介绍的均值滤波、高斯滤波，都是线性滤波方式。由于线性滤波的结果是所有像素值的线性组合，因此含有噪声的像素也会被考虑进去，噪声不会被消除，而是以更柔和的方式存在。这时使用非线性滤波效果可能会更好。中值滤波与前面介绍的滤波方式不同，不再采用加权求均值的方式计算滤波结果。它用邻域内所有像素值的中间值来替代当前像素点的像素值。

2.1.3.1OpenCv实现中值滤波

在OpenCV中，实现中值滤波的函数是cv2.medianBlur（），其语法格式如下：

         dst=cv2.medianBlur（src,ksize）

        式中：

        ● dst是返回值，表示进行中值滤波后得到的处理结果。

         ● src 是需要处理的图像，即源图像。它能够有任意数量的通道，并能对各个通道独立处理。图像深度应该是CV_8U、CV_16U、CV_16S、CV_32F 或者 CV_64F中的一种。

        ● ksize 是滤波核的大小。滤波核大小是指在滤波处理过程中其邻域图像的高度和宽度。需要注意，核大小必须是比1大的奇数，比如3、5、7等。 

2.1.3.2程序实例

import cv2  as cv
 
def cv_show(name, img):
    cv.imshow(name, img)
    cv.waitKey(0)
    cv.destroyAllWindows()
 
 
def add_peppersalt_noise(image, n=10000):
    result = image.copy()
    # 测量图片的长和宽
    w, h =image.shape[:2]
    # 生成n个椒盐噪声
    for i in range(n):
        x = np.random.randint(1, w)
        y=  np.random.randint(1, h)
        if np.random.randint(0, 2) == 0 :
            result[x, y] = 0
        else:
            result[x,y] = 255
    return result
 
 
img = cv.imread('D:\\dlam.jpg')
if img is None:
    print('Failed to read the image')
 
img1 = add_peppersalt_noise(img)
cv_show('after', img1)
 
# 中值滤波，可对灰色图像和彩色图像使用
img2 = cv.medianBlur(img1, 3)
cv_show('after1', img2)
# ksize变大图像变模糊
img3 = cv.medianBlur(img1, 9)
cv_show('after2', img3)

原图如图所示：

添加椒盐噪声：

3*3中值滤波效果： 

5*5中值滤波效果： 

         可以看出中值滤波对噪声的消除效果比线性滤波好，但是随着滤波核的增大，图像也会变模糊。

2.2变换域滤波

图像变换域滤波是对图像进行某种变换，将图像从空间域转换到变换域，再对变换域中的变换系数进行处理，之后再从变换域转换到空间域，达到降噪目的。如傅里叶变换、余弦变换、小波变换等。

2.2.1小波变换

小波阈值去噪的实质为抑制信号中无用部分、增强有用部分的过程。小波阈值去噪过程为：(1)分解过程，即选定一种小波对信号进行n层小波分解；(2)阈值处理过程，即对分解的各层系数进行阈值处理，获得估计小波系数；(3)重构过程，据去噪后的小波系数进行小波重构，获得去噪后的信号。

影响效果的主要因素有：分解层数、阈值、小波基的选择、阈值函数的选择

2.2.1.1程序实例

import pywt 
import numpy as np 
from cv2 import cv2
from PIL import Image

#==============固定阈值、预设小波=====================
img = cv2.imread("lenags15.bmp", 0)
w = 'sym4' # 定义小波基的类型
l = 3 # 变换层次为3
coeffs = pywt.wavedec2(data=img, wavelet=w, level=l) # 对图像进行小波分解
threshold = 0.04 

list_coeffs = []
for i in range(1, len(coeffs)):
    list_coeffs_ = list(coeffs[i])
    list_coeffs.append(list_coeffs_)

for r1 in range(len(list_coeffs)):
    for r2 in range(len(list_coeffs[r1])):
        # 对噪声滤波(软阈值)
        list_coeffs[r1][r2] = pywt.threshold(list_coeffs[r1][r2], threshold*np.max(list_coeffs[r1][r2])) 

rec_coeffs = [] # 重构系数
rec_coeffs.append(coeffs[0]) # 将原图像的低尺度系数保留进来

for j in range(len(list_coeffs)):
    rec_coeffs_ = tuple(list_coeffs[j])
    rec_coeffs.append(rec_coeffs_)


denoised_img = pywt.waverec2(rec_coeffs, 'sym4')
denoised_img = Image.fromarray(np.uint8(denoised_img))
denoised_img.save("result.bmp")

结果对比：

原图像：

结果图像：

 

总结：这里能够看到小波去噪对去除高斯噪声的效果还是可以的，但是效果不是很明显。大家可以从阈值的选择以及调整滤波的阈值，甚至将各层的阈值设置为不同的值再去试试。再看看有关的论文关于提升小波阈值效果的实现方法。本文只是举个简单的例子来说明小波阈值的处理过程

2.3深度学习方法

2.3.1DnCNN网络

DnCNN是图像去噪领域一篇鼻祖类型的文章，本文是关于该文章主要原理的解读。DnCNN（Denoising Convolutional Neural Network）顾名思义，就是用于去噪的卷积神经网络。

文章标题：Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising

文章链接：https://arxiv.org/pdf/1608.03981.pdf

代码链接： https://github.com/cszn/DnCNN（官方）

图像的去噪问题普遍存在，首先我们知道图像是真实世界的反映，或者说对真实世界的采样，既然是采样，难免失真，再加上采集元器件的一些不稳定性，后期得到的图像就含有更多的噪声。设理想的无噪声图像为 x ，每个像素都有一个噪声偏移量，得到的噪声图为 n ，作者把噪声产生的原因简化为下面的式子， y为添加噪声后的图像。

去噪任务的目的，就是根据噪声图像 y ，恢复出干净图像 x的过程。很显然，一个式子里未知数有两个，是有无穷多解的。传统算法通过各种滤波器算子处理噪声图像，而本文使用卷积神经网络（以下简称CNN）实现。CNN是强大的图像拟合器，把经验保存在网络中，在新样本中表现出较强的泛化性，以及比传统算法更好的去噪效果。

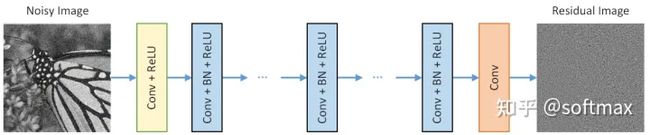
DnCNN在VGG的基础上进行修改，网络结构是（卷积、BN、ReLU）级联的结构，模型内部并不像ResNet一样存在跳远连接，而是在网络的输出使用残差学习。对于每个卷积层，采用3×3尺寸的卷积核，步长设置为1，因此，对于一个 层卷积的网络，感受野大小为  ，作者把层数设置为17，每个卷积层卷积核的数量设置为64。

模型的主要任务是，根据噪声图像 ，估计干净图像  ，但是，模型的直接输出并不是  ，而是噪声图像 ，最终干净图的获取过程用公式表达就是  。作者把这种方式称作残差学习（Residual Learning），并通过实验证实了残差学习对于提高训练稳定性和去噪效果的好处。

参考文献：

————————————————
版权声明：均值滤波部分为为CSDN博主「Justth.」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_49478668/article/details/123217030

————————————————
版权声明：高斯滤波部分为CSDN博主「Justth.」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_49478668/article/details/123485382

————————————————
版权声明：中值滤波部分为CSDN博主「Justth.」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_49478668/article/details/123485382

————————————————
版权声明：小波变换为CSDN博主「羊同学学Python」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/yy0722a/article/details/114855745

DnCNN网络：图像去噪最简单的网络之一DnCNN之讲解 - 知乎