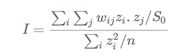GeoDa入门：安装、专题图、莫兰指数

之前写过GeoDa，不过比较分散，这里把它作为一个专题，单拎出来写。

一、GeoDa简介

GeoDa是一个免费、开源的空间数据分析软件。通过探索和建模空间模式，GeoDa向用户提供了全新的空间数据分析视角。

GeoDa支持很多空间算法，例如莫兰指数、高低聚类，支持多种文件格式，例如csv、shp等等，支持多种图表，例如折线图、散点图等等，支持多种底图，例如OSM、高德等等。

用作数据可视化和图表分析，GeoDa比QGIS更简单好用。

更多关于geoda的介绍，可参见官网：https://geodacenter.github.io/index-cn.html。

二、GeoDa安装

GeoDa安装简单，在下载页面根据操作系统的版本，下载安装包即可。

https://geodacenter.github.io/download.html

国内用户可以在gitee行下载，速度更快。

https://gitee.com/geoda/geoda_mirror/releases

下载后，双击exe文件，安装。

安装方法请参阅视频：

https://www.bilibili.com/video/BV1L64y1X7Tv/

三、GeoDa算法与学习资料

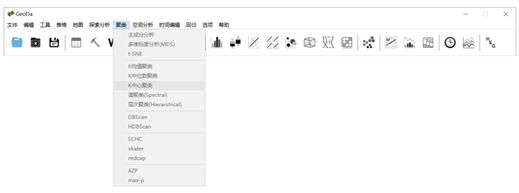
GeoDa几乎把所有空间相关的算法都集成了。

算法集中在工具条的聚类和空间分析中。

聚类是空间聚类，空间分析是量化分析。

桌面端工具很直观，我们可以拿一些数据，试试这些算法都是干什么的，有时候看书上的定义云里雾里，使用一下看结果反而就清楚了。

各种算法的原理和使用说明，在GeoDa的文档中都有。

http://geodacenter.github.io/documentation.html

文档虽然是英文的，但内容详实，操作和原理，写得比很多教科书都要清楚明白。

学习软件操作，也可以看书，例如：北京大学出版社的《空间计量分析软件：GeoDa、GeoDaSpace和PySAL操作手册》，这本书是软件开发团队写的操作指南的中译本（《Modern Spatial Econometrics in Practice: A Guide to GeoDa, GeoDaSpace and PySAL》）。英文原版亚马逊售价是71美元，京东上35元，中文书还是便宜。

原理类的，空间聚类和空间分析相关，虾神daxialu写过一版《白话空间统计》，可以看下原理和方法，这个很推荐，因为他的确写得很全面，浅显易懂，能看明白：

https://zhuanlan.zhihu.com/baihuakongjiantongji

（虾神这个系列已经完结了，一共36章。哪儿哪都好，我就是觉得他有点唠叨。）

一些教材类的书籍，说实话，我这水平，都不知道到底写的是个啥，好像中文英文都认识，但连在一起就不知道是什么了。建议大家买书的时候，优先选择外文翻译的吧。

因为空间分析是交叉学科，所以要学习原理，肯定也要学一些地理信息和统计学的书。

如果已经了解了学科基础，那么简单的学习路径应该是：

空间分析首先了解莫兰指数、P值和Z值；聚类首先了解均值聚类和密度聚类。把这几个搞懂，剩下的可以循序渐进。

四、GeoDa专题图

因为GeoDa内置了很多现成的模板，所以GeoDa制作专题图要比QGIS简单。但GeoDa毕竟不是制图软件，做不了太复杂的效果。

用北京房价shp数据，简单做一个专题图。

数据下载链接见：

https://download.csdn.net/download/sinat_41310868/18578336

或：

https://github.com/yimengyao13/qgis_tutorials

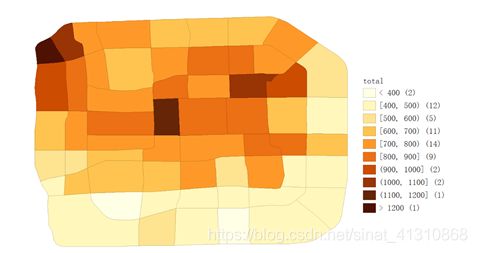
shp数据是面文件，其中total字段是房价总价，以万为单位，制作一张房价总价分布的专题图。

专题效果如下：

主要操作步骤就4个：打开文件，自定义分类，更改地图类型为自定义分类，导出PNG图片。

具体操作看视频教程，一共1分钟。

https://www.bilibili.com/video/BV1L64y1X7Tv/

五、GeoDa计算莫兰指数

我们要先了解一下啥是莫兰指数。

5-1.莫兰指数

莫兰指数是一个地学统计概念，最常用的空间自相关指标，最早由统计学家莫兰提出，所以叫做莫兰指数，很好听的名字。

莫兰指数计算公式：

其中：

看着有点晕，没关系就是个统计公式，我们只需要知道通过这个公式能计算出来莫兰指数。

莫兰指数的取值范围是[-1,1]。

莫兰指数结果如果在0到1之间，则为正相关，表示具有相似属性的对象聚集在一起。

莫兰指数结果如果在-1到0之间，则为负相关，表示具有相异属性的对象聚集在一起。

莫兰指数结果如果接近于0，则为随机分布，不存在空间自相关。

5-2.p值和z值

p值和z值都是用来表明置信度的，如果p值很小，意味着所观测的空间模式不太可能是随机的。z值表示标准差的倍数，如果z很大或很小，也意味着所观测的空间模式，不太可能是随机的。z值和p值，都与标准正态分布相关联，用来表示统计显著性，既零假设为真的情况下，拒绝零假设所要承担的风险水平，换到莫兰指数这里，零假设既是空间随机分布。

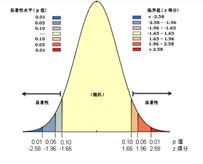
下图是一个显著性的正态分布。

把p值和z值与莫兰指数关联上，就是空间自相关性的置信度。

下表是z值、p值与置信度的关系。

5-3.GeoDa操作

软件操作不难，难的是理解数据结果。

还是用上文的shp文件，计算北京房价总价的空间自相关性。

主要操作就4步骤，打开文件、创建空间权重、计算莫兰指数、随机化。

具体看视频教程，不到1分钟。

https://www.bilibili.com/video/BV1L64y1X7Tv/

5-4.莫兰指数结果

莫兰指数为0.531，且相对成线性。

这就能看出来，房价是呈现空间自相关性的，既有相似属性的对象在空间上是聚在一起的，房价高的聚在一起，房价低的聚在一起。

5-5.随机化

随机化主要是为了对比显著性的。

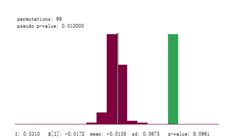
99次置换的随机化结果如下：

999次置换的随机化结果如下：

通常情况下，999次置换的结果要比99次置换的结果可靠。

我们可以看到999次置换生成的pseudo p-value是0.001，这个值的计算方式是1/（permutations+1）。

E[I]=-1/(n-1)，n是数据集中的观测值，我的对象数量是59，这个在空间权重管理界面上能看到。

mean是参考分布的平均值。

sd是参考解析的标准偏差。

z-value是标准差的倍数。

z-value越大，说明莫兰指数计算结果是强烈拒绝零假设的，既强烈拒绝随机分布。

以999次随机化的z-value的值7.7589，参照z值、p值与置信度的关系，置信度应该有99%。

5-6.综合结论

99%的可能性，北京的房价是有空间正相关性的。

莫兰指数计算的也是统计结果，统计结果就存在概率问题。

我们使用的数据，只是一份样本数据，我之前拿密度更高的全量数据计算，全局莫兰指数是0.997，z值是901.8945，莫兰指数更趋近于1，z值更大。说明北京房价是空间正相关的，房价高的小区挨在一起，房价低的小区挨在一起。这跟我们的认知是相符的。

六、总结

软件操作还是挺简单的，难的是理论上的，莫兰指数、p值和z值，想要了解理论，最好的方式，还是看书。