MATLAB解算坐标转换7参数
文章目录
- 前言
- 一、WGS_84与XIAN_80转换七参数说明
-
- 1、两种坐标系统说明
- 2、七参数求解公式(布尔莎模型)
-
- (1)七参数
- (2)布尔莎模型
- 3、转换流程
- 二、MATLAB代码实现以及解释
-
- MATLAB代码
- 程序运行结果
前言
1、布尔莎七参数模型一直被广泛用于测绘领域,不仅仅是几大常用坐标系统之间的七参数、或者是两个独立(建筑)坐标系统之间的七参数,其都可以利用最小二乘求解的方法进行解算。
2、MATLAB作为数学计算编程软件的天花板,其高精度的数据处理方式和简易的语言风格,一直以来很受欢迎。此处,我利用MATLAB作为平台以及布尔莎七参数模型,对WGS_84到XIAN_80两个坐标系统的七参数进行解算。
3、如有错误,还望各位指正,谢谢
一、WGS_84与XIAN_80转换七参数说明
1、两种坐标系统说明
WGS_84坐标系:
其属于地心坐标系,坐标原点位于地球质心,z轴指向BIH1984定义的地级CTP方向,x轴指向BIH1984定义的零子午面和CTP赤道的交点,y轴与xz组成右手坐标系,是世界大地坐标系统。
XIAN_80坐标系:
其属于参心坐标系,坐标原点位于陕西省泾阳县永乐镇,x轴在大地起始子午面内与z轴垂直指向经度0方向,其主要的参数采用国际标准,y轴与xz组成右手坐标系,是中国在1980年设立的全国大地坐标系统。
| 椭球参数 | 长半轴a | 短半轴b | 扁率a | 第一偏心率 |
|---|---|---|---|---|
| WGS84椭球 | 6378137±2(m) | 6356752.3142 (m) | 1/298.2572236 | 0.00669437999013 |
| XIAN80椭球 | 6378140±5(m) | 6356755.2882(m) | 1/298.2570 | 0.00669438499959 |
在此处需要说的就是,由于地球椭球是数学体面,所以其实常见的几种大地坐标系统其椭球参数都相差无几。
| 坐标形式 | x’ | y’ | z ’ | 坐标类型 |
|---|---|---|---|---|
| 地理大地坐标 | L(经度) | B(纬度) | H(大地高) | 数学坐标系 |
| 投影平面坐标 | y | x | z(水准高) | 投影坐标系 |
| 空间直角坐标 | X | Y | Z | 数学坐标系 |
2、七参数求解公式(布尔莎模型)
(1)七参数
本次利用的是WGS84以及XIAN80分别的三个空间直角坐标系计算的七参数
备注:
若源数据为BLH地理坐标系,可参考的我上一个文章,里面有经纬度转空间直角坐标的转换过程和源码;
若源数据为xyz投影坐标系,可以自行寻找高斯反算的流程和代码进行转换,我将于不久之后发布高斯反算
所谓七参数,就是两个坐标系之间的转换参数,通常用7个参数形式来表示,分别是:
坐标平移参数(dx,dy,dz): ---------原点O1相对于原点O2的平移距离,单位m
坐标旋转参数(rx,ry,rz):---------该坐标系的三个坐标轴相对于另一坐标系的三个坐标轴的旋转角度的余弦值
坐标尺度因子(m):---------该坐标系与另一坐标系之间的尺度变化因子,一般都是无限接近于0,所以一般用(1+m’)表示,程序中m=m’+1
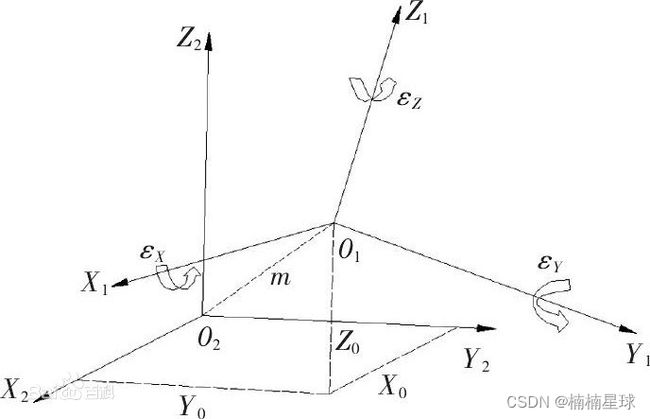 七参数图示(来源百度百科) 七参数图示(来源百度百科)
|
(2)布尔莎模型
所谓布尔莎(Bursa)模型,俗你七参数转换法,是用来转换两个不同椭球之间相应点坐标,因为每个点有坐标和高程,所以最少有三个点才能解算,多余的点要用最小二法求最或然值
 图1 线性矩阵形式表示 图1 线性矩阵形式表示
|
 图2 方程组形式表示 图2 方程组形式表示
|
3、转换流程
- 源数据:
由于布尔莎模型中含有7个参数,因此需要至少3组或3组以上的数据进行计算,留1组进行最后的验证工作。
在下面的txt文件8行数据中,前4行表示4个点WGS_84坐标系的空间直角坐标,后4行表示该4点在XIAN _80坐标系的空间直角坐标

- 带入公式最小二乘求参:
由于MATLAB中最小二乘拟合参数的函数很难对高维空间的!多元一次方程组!进行解算,或许是我技术不精没有找到相关函数,故利用普通方法解算,希望读者能够理解
由于数据和涉及的参数比较多,我这里就说一下大概流程,具体可以参考代码
1、将3个点的坐标数据分别带入布尔莎方程组,可以产生9个公式
2、根据最小二乘原理,将上面的9个公式进行移项并分别整体平方,然后相加赋值给S,形成一个总的公式
3、利用此公式对7个参数进行求偏导并分别赋值为0,可产生9个公式
4、将这9个公式联立解得7个参数的值
二、MATLAB代码实现以及解释
程序清单:
importdata函数: 以文件的方式读取文件
diff函数(a=diff(s,b)): 利用公式s对b求偏导,如果s是多元方程,则a的结果是一个式子
solve函数(a=solve(s)): 解算公式s的值,并赋值给a
format long g: 临时关闭科学计数法,以双精度或者浮点数的形式输出
MATLAB代码
clc;
clear all;
filename=importdata("WX_XYZ.txt");
WGS_X=double(filename.data(1:3,1));
WGS_Y=double(filename.data(1:3,2));
WGS_Z=double(filename.data(1:3,3));
XIAN_X=double(filename.data(5:7,1));
XIAN_Y=double(filename.data(5:7,2));
XIAN_Z=double(filename.data(5:7,3));
% X2=dx+m*x1-ry*z1+rz*y1;
% y2=dy+m*y1+rx*z1-rz*x1;
% z2=dz+m*z1-rx*y1+ry*x1;
% y=kx+b
syms dx dy dz m rx ry rz gg
gg(1)=WGS_X(1)-(dx+m*XIAN_X(1)-ry*XIAN_Z(1)+rz*XIAN_Y(1));
gg(2)=WGS_X(2)-(dx+m*XIAN_X(2)-ry*XIAN_Z(2)+rz*XIAN_Y(2));
gg(3)=WGS_X(3)-(dx+m*XIAN_X(3)-ry*XIAN_Z(3)+rz*XIAN_Y(3));
gg(4)=WGS_Y(1)-(dy+m*XIAN_Y(1)+rx*XIAN_Z(1)-rz*XIAN_X(1));
gg(5)=WGS_Y(2)-(dy+m*XIAN_Y(2)+rx*XIAN_Z(2)-rz*XIAN_X(2));
gg(6)=WGS_Y(3)-(dy+m*XIAN_Y(3)+rx*XIAN_Z(3)-rz*XIAN_X(3));
gg(7)=WGS_Z(1)-(dz+m*XIAN_Z(1)-rx*XIAN_Y(1)+ry*XIAN_X(1));
gg(8)=WGS_Z(2)-(dz+m*XIAN_Z(2)-rx*XIAN_Y(2)+ry*XIAN_X(2));
gg(9)=WGS_Z(3)-(dz+m*XIAN_Z(3)-rx*XIAN_Y(3)+ry*XIAN_X(3));
ss=(gg(1))^2+(gg(2))^2+(gg(3))^2+(gg(4))^2+(gg(5))^2+(gg(6))^2+(gg(7))^2+(gg(8))^2+(gg(9))^2;
s_dx=diff(ss,dx)==0;
s_dy=diff(ss,dy)==0;
s_dz=diff(ss,dz)==0;
s_m=diff(ss,m)==0;
s_rx=diff(ss,rx)==0;
s_ry=diff(ss,ry)==0;
s_rz=diff(ss,rz)==0;
[dx,dy,dz,m,rx,ry,rz]=solve(s_dx,s_dy,s_dz,s_m,s_rx,s_ry,s_rz);
check_X=dx+m.*(filename.data(8,1))-ry.*(filename.data(8,3))+rz.*(filename.data(8,2));
check_Y=dy+m.*(filename.data(8,2))+rx.*(filename.data(8,3))-rz.*(filename.data(8,1));
check_Z=dz+m.*(filename.data(8,3))-rx.*(filename.data(8,2))+rz.*(filename.data(8,1));
wucha_xx=(check_X-filename.data(4,1));
wucha_yy=(check_Y-filename.data(4,2));
wucha_zz=(check_Z-filename.data(4,3));
format long g;
result=[];
result(1,:)=[double(dx),double(dy),double(dz)];
result(2,:)=[double(rx),double(ry),double(rz)];
result(3,:)=[double(m),str2double('null'),str2double('null')];
result(4,:)=[double(check_X),double(check_Y),double(check_Z)];
result(5,:)=[double(filename.data(4,1)),double(filename.data(4,2)),double(filename.data(4,3))];
result(6,:)=[double(wucha_xx),double(wucha_yy),double(wucha_zz)]
% xlswrite('C:\Users\稳魂\Desktop\result.xls',result);
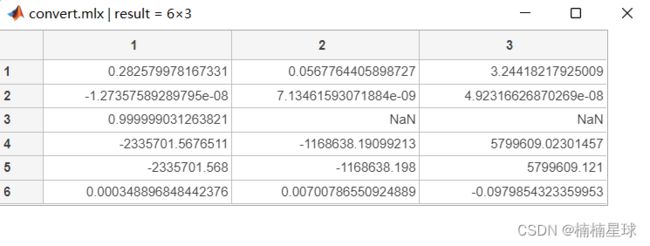
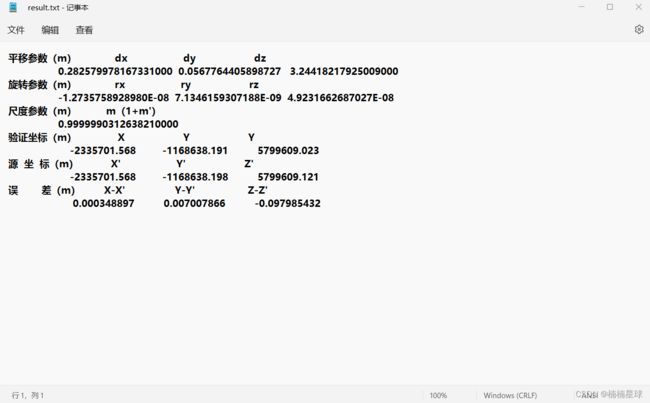
程序运行结果
我们可以将其输出为xls表格文件(最后一行代码),加以编辑成txt文档,可以观察到本次七参数计算结果