【前缀和】算法实战
文章目录
- 一、算法原理
-
- 1. 一维前缀和
- 2. 二维前缀和
- 二、算法实战
-
- 1. leetcode560 和为K的子数组
- 2. leetcode974 和可被K整除的子数组
- 3. leetcode525 连续数组
- 4. leetcode1314 矩阵区域和
- 5. leetcode724 寻找数组的中心下标
- 6. leetcode238 除自身以外数组的乘积
- 三、总结
一、算法原理
前缀和算法指的是某段序列的前n项和,前缀和一般用来求数组中某段连续区间的和。下面我们来看一下它的算法原理。
1. 一维前缀和
思路:
先预处理一个前缀和数组:dp[i] 表示 [1, i] 区间内所有元素的和。dp数组的递推公式为:dp[i] = dp[i - 1] + arr[i];这里我们的数组下标从1开始是为了处理边界情况。
使用前缀和数组:[ l , r ]区间和 = dp[ r ] - dp[ l - 1 ];
代码实现:
#include 2. 二维前缀和
思路:
类⽐于⼀维数组的形式,如果我们能处理出来从 [0, 0] 位置到 [i, j] 位置这⽚区域内所有元素的累加和,就可以在 O(1) 的时间内,搞定矩阵内任意区域内所有元素的累加和。因此我们接下来仅需完成两步即可:
- 第⼀步:搞出来前缀和矩阵
这⾥就要⽤到⼀维数组⾥⾯的拓展知识,我们要在矩阵的最上⾯和最左边添加上⼀⾏和⼀列,这样我们就可以省去⾮常多的边界条件的处理(同学们可以⾃⾏尝试直接搞出来前缀和矩阵,边界条件的处理会让你崩溃的)。处理后的矩阵就像这样:

这样,我们填写前缀和矩阵数组的时候,下标直接从 1 开始,能⼤胆使⽤【i - 1 , j - 1】 位置的值。 - 递推方程
递推⽅程就是:sum[i][j]=sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1]+matrix[i - 1][j - 1] - 使用前缀和矩阵:

目标矩阵的面积 =dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]
代码实现:
#include 二、算法实战
1. leetcode560 和为K的子数组
解题思路:前缀和 + 哈希表
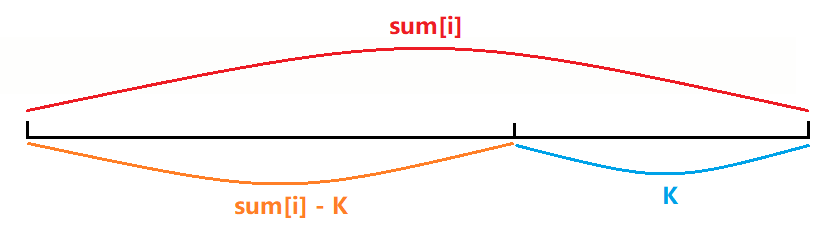
我们可以将这个问题的求解转换一下,这道题的原意是让我们求以i为结尾的所有满足要求的子数组,我们可以将问题转换为:在[0, i - 1]区间内,有多少前缀和等于sum[i] - k。
我们建立哈希表,以和为键,出现的次数为对应的值,记录prev[i]出现的次数,那么以 i 结尾的答案 mp[pre[i]−k] 即可在 O(1) 时间内得到。由于prev[i]的计算只与前一项的答案有关,因此我们直接用prev变量来记录答案即可。
这里有一个细节问题,如果整个前缀和等于K需要特殊处理一下,我们需要提前让hash表中的hash[0] = 1;
代码实现:
// 写法一:
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int,int> hash;
int pre = 0, cnt = 0;
hash[0] = 1;
for(auto& e : nums)
{
pre += e;
if(hash.find(pre - k) != hash.end())
cnt += hash[pre - k];
hash[pre]++;
}
return cnt;
}
};
// 写法二:
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int n = nums.size();
vector<int> pre(n + 1);
for(int i = 1; i <= n; i++)
pre[i] = pre[i - 1] + nums[i - 1];
unordered_map<int,int> hash;
int res = 0;
hash.insert({0, 1});
for(int i = 1; i <= n; i++)
{
res += hash[pre[i] - k];
hash[pre[i]]++;
}
return res;
}
};
2. leetcode974 和可被K整除的子数组
补充知识:同余定理+(C++、Java)中[负数%正数]的结果以及修正
解题思路:前缀和+哈希表
这道题和上一道题目很相似。一个是求和为k的子数组,一个是求和可被k整除的子数组,方法是一样的。首先使用pre变量来遍历数组存储到目前为止的前缀和,根据同余定理,只需要满足pre[j] mod K == pre[i-1] mod K即可。
我们可以考虑对数组进行遍历,在遍历同时统计答案。当我们遍历到第 i 个元素时,我们统计以 ji 结尾的符合条件的子数组个数。然后维护一个以前缀和模 K 的值为键,出现次数为值的哈希表 ,在遍历的同时进行更新。这样类似上一题进行维护和计算即可得到结果。
代码实现:
class Solution {
public:
int subarraysDivByK(vector<int>& nums, int k) {
unordered_map<int,int> hash;
int pre = 0, cnt = 0;
hash[0] = 1;
for(auto& e : nums)
{
pre += e;
int r = ((pre - k) % k + k) % k;
if(hash.find(r) != hash.end())
cnt += hash[r];
hash[r]++;
}
return cnt;
}
};
3. leetcode525 连续数组
解题思路:前缀和+哈希表
根据题意可得,数组中的元素不是0就是1,题目要求我们找到含有相同数量的 0 和 1 的最长连续子数组,那么我们可以转化一下思路:1. 将所有的0修改为-1。2. 在数组中找出最长的子数组,使数组中所有元素的和为0。
这里我们还是使用前缀和+哈希表的方式来解决。在哈希表中存的是前缀和的末尾元素的下标。当哈希表中有重复的【后者-前者】区间内的元素之和为0。这时,我们使用一个Max变量来更新我们的结果即可。当然,区间长度=[当前下标-前一个前缀和等于0的末尾元素下标],否者则将该前缀和的末尾元素下标丢入哈希表即可。这保证了我们如果有重复的hash[0]=-1。
代码实现:
class Solution {
public:
int findMaxLength(vector<int>& nums) {
unordered_map<int, int> hash;
int pre = 0, Max = 0;
hash[0] = -1;
for(int i = 0; i < nums.size(); i++)
{
if(!nums[i]) nums[i] = -1;
pre += nums[i];
if(hash.count(pre))
Max = max(Max, i - hash[pre]);
else
hash[pre] = i;
}
return Max;
}
};
4. leetcode1314 矩阵区域和
解题思路:二维前缀和
首先我们需要读懂题目的含义,我们需要将原数组的每个元素变成对应矩阵范围的区域和,为了能够快速求出矩阵某段区域的面积之和。因此我们需要构造前缀和数组。
因为我们所学习的前缀和数组下表是从1开始的,但是在力扣中的数组的下标都是从0开始的,所以我们构造前缀和数组时需要将前缀和数组在原数组的基础上添加一行一列,以便于后续好处理。
但是这道题目真正的难点在于下标之间的关系,因为前缀和数组的下标是从1开始的,但是我们所求的目标数组又是从0开始的,所以这之间就必须要存在一种转换关系,需要我们自己把握。
代码实现:
class Solution {
public:
int getRet(int x1, int x2, int y1, int y2)
{
return tmp[x2][y2] - tmp[x1 - 1][y2] - tmp[x2][y1 - 1] + tmp[x1 - 1][y1 - 1];
}
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
int n = mat.size(), m = mat[0].size();
tmp = vector<vector<int>>(n + 1, vector<int>(m + 1));
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
tmp[i][j] = tmp[i - 1][j] + tmp[i][j - 1] - tmp[i - 1][j - 1] + mat[i - 1][j - 1];
// 目标数组
vector<vector<int>> ret(n, vector<int>(m));
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++){
int x1 = max(i - k, 1);
int x2 = min(i + k, n);
int y1 = max(j - k, 1);
int y2 = min(j + k, m);
ret[i - 1][j - 1] = getRet(x1, x2, y1, y2);
}
return ret;
}
private:
vector<vector<int>> tmp; // 前缀和数组
};
5. leetcode724 寻找数组的中心下标
解题思路:
题目要求我们求解数组的中心下标,中心下标的定义为:其左侧所有元素相加的和等于右侧所有元素相加的和。根据题目的这个意思,我们可以构建前缀和数组。我们可以根据:左侧元素相加之和=dp[n - 1] - dp[i],右侧元素相加之和=dp[i-1],我们使用左侧元素减去右侧元素之和,看结果是否为0,如果为零,该位置则为数组的中心下标。当然我们需要注意边界情况特殊处理一下即可。
代码实现:
class Solution {
public:
int pivotIndex(vector<int>& nums) {
int ret = -1, n = nums.size();
int dp[10001] = {0};
for(int i = 0; i < n; i++){
if(i == 0) dp[0] = nums[0];
else dp[i] = dp[i - 1] + nums[i];
}
for(int i = 0; i < n; i++)
{
int tmp = 0;
if(i == 0)
tmp = dp[n - 1] - nums[i];
else if(i == n - 1)
tmp = dp[n - 1] - nums[n - 1];
else
tmp = dp[n - 1] - dp[i] - dp[i - 1];
if(tmp == 0)
return i;
}
return ret;
}
};
6. leetcode238 除自身以外数组的乘积
解题思路:
这道题的要求是让我们将数组中的每个元素变成除了它自身外其他元素之积,我们可以根据前缀和的思想,构造两个数组:前缀积数组和后缀积数组。前缀积数组: f[i]表示 [0, i-1] 区间内所有元素的乘积。后缀积数组: g[i]表示 [i+1, n-1] 区间内所有元素的乘积。我们求目标数组的元素时直接 ret[i] = f[i] * g[i] 即可。
当然这道题目我们还可以使用滚动数组进行优化,原本需要开三个数组,但是优化后只需要一个数组就可以解决。先开一个前缀积数组,然后求出前缀积。然后接下来for循环从后往前遍历,因为后缀积数组的后一项可以推出前一项,所以使用一个临时变量right来依次滚动推导每一次需要使用的后缀积,然后乘以前缀积数组中的元素,就可以直接将前缀积数组推导成为目标数组。
代码实现:
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
if(n == 0) return {};
vector<int> ret(n, 0);
ret[0] = 1;
for(int i = 1; i < n; i++)
{
ret[i] = ret[i - 1]*nums[i - 1];
}
int right = 1;
for(int i = n - 1; i >= 0; i--)
{
ret[i] *= right;
right *= nums[i];
}
return ret;
}
};
三、总结
在算法题中,前缀和计算时间复杂度为O(n),后续要查询对应的操作算法复杂度为O(1),使用前缀和后,能大大减少算法复杂度。同时,前缀和属于「空间换时间」的算法或者也可以说不是算法,而是一种数组的「预处理」。