C语言总谐波失真（THD）实现，从理论到应用分析改进详解

引言

从Matlab总谐波失真（THD）仿真到C语言总谐波失真（THD）应用

对于如何实现THD，上篇文章中已经叙述的比较清晰，但是，正如结尾中表述，实际计算数据与理论数据差距过大，无法应用在实际的系统中，所以有了这篇文章，目的就是分析和解决FFT过程中产生的频谱泄露和栅栏效应问题

因为THD对FFT生成后的幅频特性曲线要求严格，因此需要对于窗和插值的使用也要小心。

下面依然是从测试信号生成开始讲起

测试信号生成

为了更好的分析THD，依然是生成一个测试正弦信号

通过matlab生成，然后再去使用au软件进行处理

M=8192*8;%fft采样点
Fs=48000; %采样频率，一秒多少个采样点
N=48000*4; %序列长度，总数据有多少个点
f1=100;                 
f2=200;
f3=300;
T=1/Fs; %单个点采样时间
t=(0:1:N-1)*T; %总时间T/Fs，每个点时间间隔t 
y=0.1*sin(2*pi*f1*t-pi/6)+0.0001*sin(2*pi*f2*t+pi/2)+0.0001*sin(2*pi*f3*t+pi/3);  %生成输入信号
% % y=6*sin(2*pi*f1*t+pi/3);
% figure(1)
% plot(t, y);

% y = awgn(y, 0, 'measured');
% 存储信号到wav文件
filename = 'sine_24bit_48k.wav';
audiowrite(filename, y, Fs, 'BitsPerSample', 24);

[y, Fs] = audioread('sine_24bit_48k.wav');    %读取wav文件
figure
plot(t, y);

Y = fft(y, M); %作FFT变换
A = abs(Y); %计算幅值
figure
% plot(0:1:(N-1)/2, A(1:N/2));
plot(0:1:M-1, A(1:M));title('Matlab N=131,072');xlabel('N');ylabel('Amplitude');%作图

最终生成一个24位，48khz的wav文件

wav音频文件解析读取 定点转浮点分析 幅值提取（C语言实现）

正如此篇文章，对于wav文件解析以及提取就不再赘述

THD分析

因为FFT采用的是基2-FFT，因此FFT采样点均选择2的整数次幂，因此截断信号很难会是整数周期

采样点选择

对于THD，原理上没有什么可深挖的，就是谐波能量与基波能量的比值，公式变形后就是谐波分量的幅值平方和相加再开根，然后比上基波的幅值

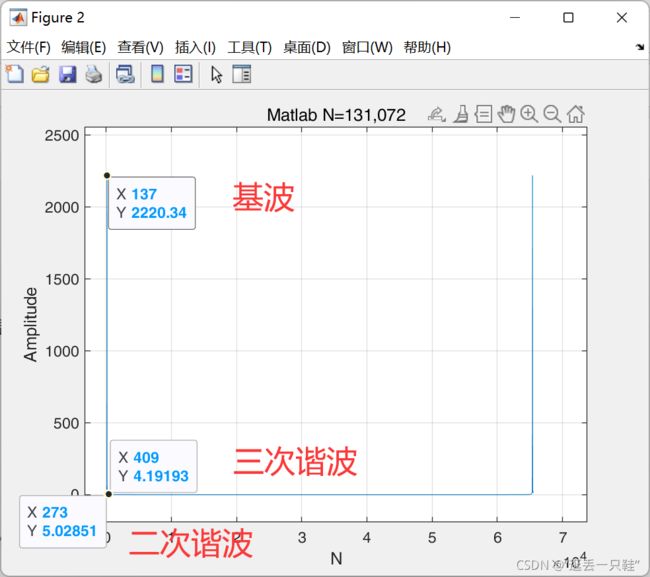
对与理想的信号源以及FFT后，应该出现的是如上图所示的频谱图，所以在我们之前的C语言代码中，简单粗暴的只要频谱图中这个信号是高于两侧信号，就认为这个是谐波信号。

但是，对于这么一个24位的wav音频文件，我们得到的实际fft后信号没有这么的完美。

罪魁祸首就是采样点导致的频率分辨率的问题

我们这段信号采用频率为48000Hz，FFT的采样点为 8192*8 = 65536，按理来说，频率分辨率为 48000 / 65536 = 0.732421875

所以，对于正弦信号来讲基波的理论频域频率点应该是 100 / 0.732421875 = 136.5333

理论频域中的幅值应该是 0.1 * 65536 / 2 = 32768

但是实际基波的值为 频率点 137，频率幅值 2220.34

频率点值还好，差别不大，可以忽略误差，但是对于频率的幅值来讲，简直就是灾难，如果使用实际中基波频域的幅值去换算时域的幅值，得到的是 2220.34 / 65536 * 2 = 0.067759399 ，与理论值的0.1幅值相比相差甚远。

除了这个问题，在采样点为65536的程序中还存在一个BUG

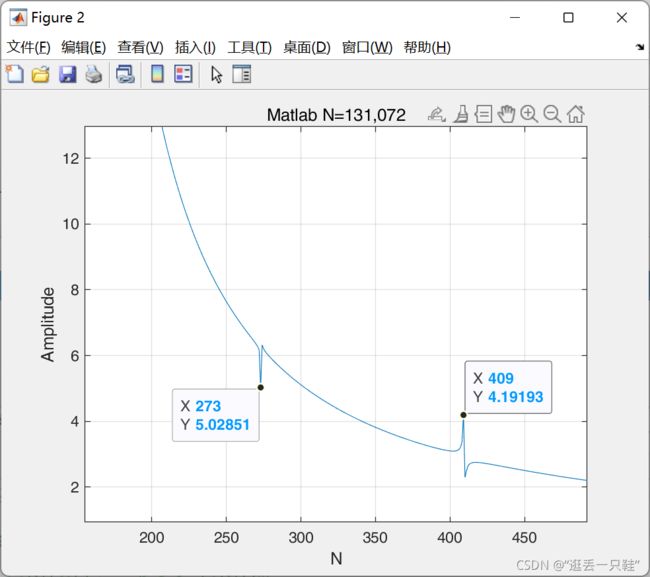
例如在频谱图中的点273处

我们可以看到不同于我们一般见到的谐波信号是一个脉冲，这里是一个凹陷，这就是矩形窗带来的一个后果，主瓣衰减太慢了，影响了其他信号

这里虽然不是脉冲信号，但是，根据谐波是基波频率的整数倍的原理，我们知道在273频点上就是我们的二次谐波

这个其实也是频率分辨率为0.7和矩形窗一起带来的偏差，在这里显示的非常直观和清晰

虽然看起来我们的频率分辨率比频率分辨率为1时候更加精准了

但是因为采样的是非整周期信号，所以还是会导致栅栏效应

脉冲信号消失问题

所以，针对这个问题，解决方法就在FFT采样点的选择上，因为罪魁祸首就是截断信号不是整周期信号！

在matlab仿真的过程中，采样点选择65536，按理来说处理一个采样频率为48000采样率的信号绰绰有余，但是现实就是无情的打脸（基础不牢和受制于C语言中基2的FFT算法）

因此，增加FFT的采样点，这一次增加到 8192*16 = 131,072

现在频率的分辨率来到了 48000 / 131072= 0.3662109375

这时候我们再来看频谱图

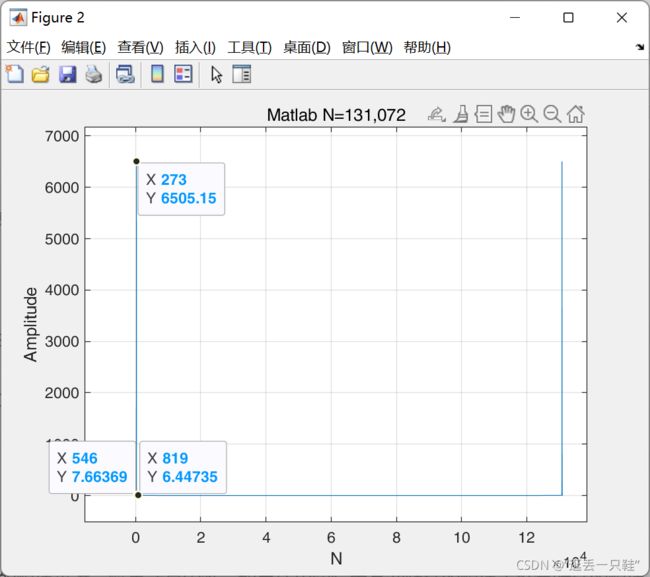
现在对这个采样点又增加了一倍的正弦信号分析

对于正弦信号来讲基波的理论频域频率点应该是 100 / 0.3662109375 = 273.0666666666666

理论频域中的幅值应该是 0.1 * 131072/ 2 = 6,553.6

但是实际基波的值为 频率点 273，频率幅值 6505.15，根据实际基波逆推得到的时域频率为 99.9755859375，时域幅值为 0.099260711669921875

这一次，我们终于正儿八经的接近了正确的答案，得到了理想的值

不过，这里还有一个问题

幅值不等问题

/ * 2021/11/30 更新 * /

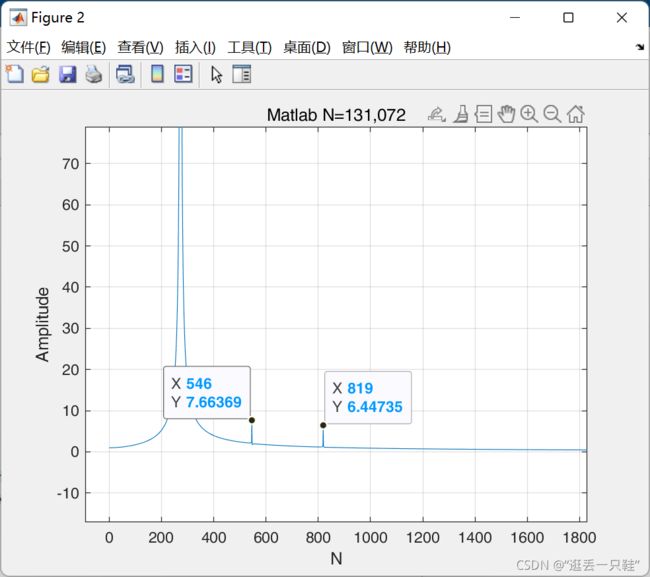
对于图中的两个点，按理论来讲，频率点没有任何问题，但是幅值出现了异常，因为这两个频率点的幅值应该是完全一致

而图中的幅值却相差20%左右，虽然经过转换后时域中幅值不会相差太多，但是仍然是个非常大的隐患

这个现象应该是出现了频率泄露，需要对信号进行加窗的操作。

FFT频谱分析（补零、频谱泄露、栅栏效应、加窗、细化、频谱混叠），Matlab、C语言代码

这篇文章中整理了FFT频谱分析会遇到的几乎全部问题，可以先行跳转

经过理论知识的补全

我们在FFT变换过程中，如果采样点和采样频率不相同，即没有取到完整的函数周期倍数，那么就会造成频谱泄露

对于频谱泄露，一般采取的方法步骤为加窗，然后插值，在进行FFT

加窗

在大量的论文阅读后，加窗是改善频谱泄露的好方法，在Matlab中进行仿真验证

clc;clear;close all;


fs=48000; %采样频率，一秒多少个采样点
M=8192*8; %序列长度，总数据有多少个点
f1=100;                 
f2=200;
f3=300;
T=1/fs; %单个点采样时间
t=(0:1:M-1)*T; %总时间T/Fs，每个点时间间隔t 
x=0.1*sin(2*pi*f1*t-pi/6)+0.0001*sin(2*pi*f2*t+pi/2)+0.0001*sin(2*pi*f3*t+pi/3);  %生成输入信号

% [x, fs] = audioread('sine_24bit_48k.wav');

N = 8192*8;                       %设置短时傅里叶变换的长度，同时也是汉明窗的长度
h = hamming(N);                   %设置汉明窗 1.36
%sprintf("%d",h);
for m=1:N                         %用汉明窗截取信号，长度为N，主要是为了减少截断引起的栅栏效应等
    b(m)=x(m)*h(m);
end

for mm=1:N
    y1(mm)=x(mm);
end

subplot(3,1,1),plot(t, x);title('original signal');
T=1/fs;                         %单个点采样时间
t=(1:1:N)*T;                    %总时间T/Fs，每个点时间间隔t 
subplot(3,1,2),plot(t, y1);title('window function signal');
subplot(3,1,3),plot(t, b);title('hamming added signal');
grid on
figure

% ya=20*log10(abs(fft(y1)));        %做傅里叶变换，取其模值，即幅频特性，然后用分贝（dB）表示
ya=abs(fft(y1, N));
subplot(2,1,1),                     %分配画布，一幅图上共两个图，这是第一个
plot(ya);title('window function signal');  %画出原始信号，即前面这个音频信号的原始波形
grid                                %添加网格线


% y=20*log10(abs(fft(b)));          %做傅里叶变换，取其模值，即幅频特性，然后用分贝（dB）表示
y=abs(fft(b, N));
subplot(2,1,2),                     %分配画布，第二副图
plot(y);title('hamming added signal');            %画出短时谱
grid

绘制出效果图

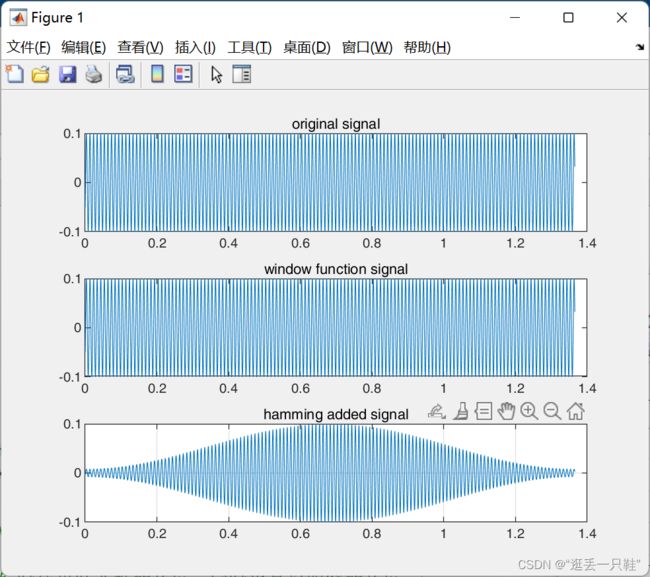
可以看到加窗后频率点274 和 410 的幅值一致了

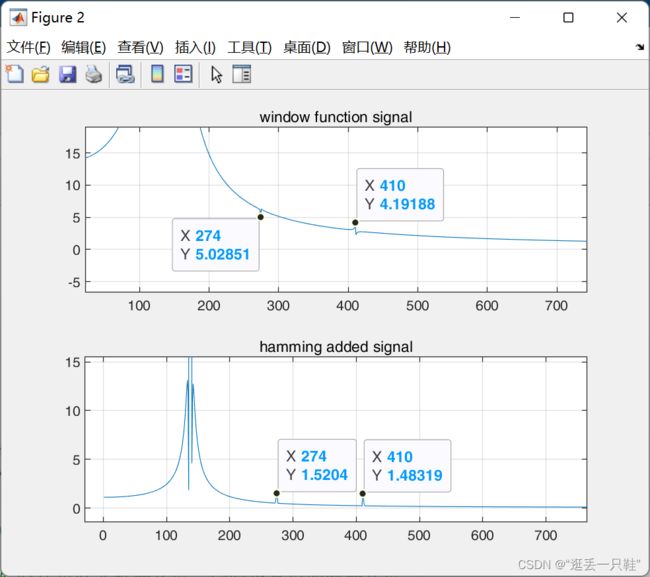
但是，仔细观察会发现，原来的基波主瓣虽然变窄了，但是多了两个明显的旁瓣，并且所有频率点的幅值都变小了

这就是加窗会带来的后果，虽然总的能量不变，但是会使得能量向周围泄露，因此要想还原时域中的幅值，就需要进行幅值的修正

经过一系列的调研，发现幅值的修正虽然理论可行，但是对于C语言实现需要大量的实验测试才能的出来一个比较好的结果

并且C语言实现工作量较大，所以加窗后插值的方法虽然在Matlab仿真实现，最后还是没有采用

还是可以看到，加窗后插值对于频谱改善还是非常的明显，并且因为插值成了整数倍，采样点也满足了整周期

插值

因此，对于加窗，虽然改善了幅频特性，但是也带来了很多麻烦

因此加窗虽然改善了幅频特性，但是也导致我需要的幅值发生了变化，还需要投入更大的精力去修正

这时我回想起了频谱泄露和栅栏效应最初的原因

没有取到完整的周期进行FFT

因为FFT算法使用基2的方法，采样点被限制在了2的整数次幂

而采样信号的频率为48000Hz，附近的整数次幂也只有 32768 和 65536

所以，既然没有办法对480000个点直接进行基2的FFT，那么就先取48000个点，然后通过插值算法插值到65536个点，再进行65536个点的FFT使得截断信号变成整周期

clc;clear;close all;

M=8192*8;%fft采样点
% M = 48000;
Fs=48000; %采样频率，一秒多少个采样点
N=48000*2; %序列长度，总数据有多少个点
f1=100;                 
f2=f1 * 2;
f3=f1 * 3;
T=1/Fs; %单个点采样时间
t=(0:1:N-1)*T; %总时间T/Fs，每个点时间间隔t 
y=0.1*sin(2*pi*f1*t-pi/6)+0.0001*sin(2*pi*f2*t+pi/2)+0.0001*sin(2*pi*f3*t+pi/3);  %生成输入信号
% % y=6*sin(2*pi*f1*t+pi/3);

% y = awgn(y, 20, 'measured');
% % 存储信号到wav文件
filename = 'sine_24bit_48k.wav';
audiowrite(filename, y, Fs, 'BitsPerSample', 24);

[y, Fs] = audioread('sine_24bit_48k.wav');    %读取wav文件
figure
plot(t, y);
% y = xlsread('test_data.xlsx');

y = y(1:48000);
% h = hamming(48000);                   %设置汉明窗 1.36
% %sprintf("%d",h);
% for m=1:48000                         %用汉明窗截取信号，长度为N，主要是为了减少截断引起的栅栏效应等
%     y(m)=y(m)*h(m);
% end
% t1 = 0: 1/Fs : (48000-1)/Fs;
% t2 = 0: 1/Fs/(8192*8/48000.0) : (48000-1)/Fs;%通过插值，提高48000Hz频率到65536Hz
for ii = 1:48000
    t1(ii) = ii;
end
for ii = 1:65536
    t2(ii) = ii*48000/65536.0;
end
y = interp1(t1, y, t2, 'spline');
y = y .';


% Matlab FFT
Y = fft(y, M); %作FFT变换
% A = 20*log10(abs(Y)); %计算幅值
A = abs(Y);
figure
% plot(0:1:(N-1)/2, A(1:N/2));
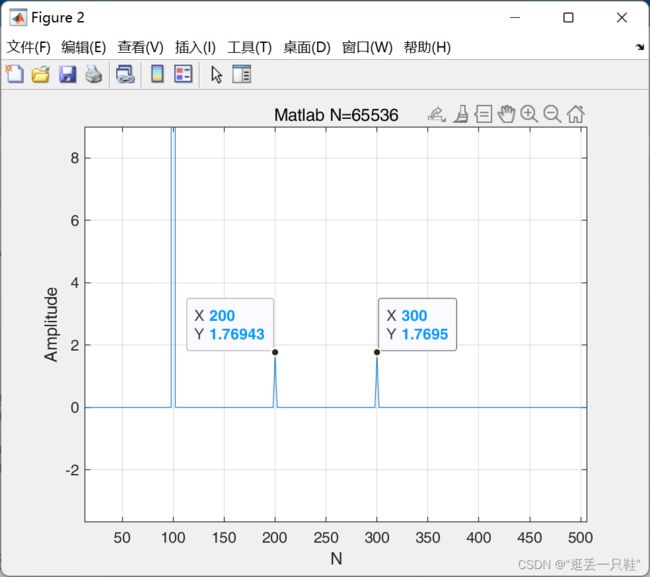
plot(0:1:M-1, A(1:M));title('Matlab N=65536');xlabel('N');ylabel('Amplitude');%作图
grid on

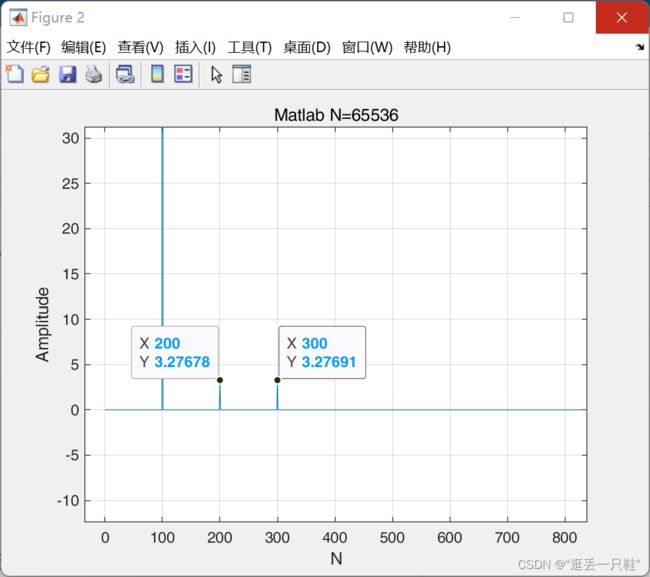
对于频率点100

3276.8 / 65536 * 2 = 0.1

对于频率点200

3.27678 / 65536 * 2 = 0.0000999993896484375

对于频率点300

3.27691 / 65536 * 2 = 0.00010000335693359375

这个结果不能所示差不多吧，只能说是完全符合预期！

并且因为只是从48000插值到了65536，插值的影响对原信号不是那么的大，所以因为插值本身引起的误差就很小

插值后可以对整周期点数进行FFT，所以也不会出现栅栏效应和频谱泄露

至此，问题粗暴的解决！

代码实现

有了充足的理论支撑，我们可以对C语言进行大刀阔斧的动手了

需要注意的有以下几点

1. 基波的判断，要先把所有的频域分量找出来，然后找到幅值最大的那个基波，一个是得到频域的幅值，另一个就是得到频域的频率点
2. 谐波的判断，首先谐波要在基波时域频率的整数倍上，其次谐波除了要比两边的频率点幅值大，还要保证不是误差引起的只是大了一丢丢的意外

下面的代码是相关的核心代码，对上篇文章出现的问题进行了有效的改进，肯定没有办法直接用，但是提供一个小思路

#define PI          acos(-1)
#define N           48000*4                     // 输入数据长度
#define Fs          48000
#define M           8192*8                      // FFT 采样点 2的n次幂
#define Mn          16                          // FFT 采样点次幂数 2^Mn

void THD_TEST_Pthread(void)
{  
    while(1) {
        
        if(fft_flag == 1) {

            int i = 0, j = 0;
            double T = 1.0 / Fs;
            double pr[N];
            double pi[N], fr[N], fi[N], t[N];

            int z = 0;
            int fft_data_n[1024], denominator_n = 0;
            double fft_data_a[1024];
            double molecule = 0.0, denominator = 0.0, thd = 0.0;
            double direct_frequency = 0.0, direct_amplitude = 0.0;
            int temp = 0;
            char thd_data[4];
            int ret = 0;
            double *wavdata;

            FILE *fp_fftdata, *fp_sine;                 //文件指针

            fp_fftdata=fopen("fftdata.txt","w");  
            if(fp_fftdata==NULL) {       
                printf("File cannot open! " );
                exit(0);
            }
            fp_sine=fopen("sinedata.txt","w");  
            if(fp_sine==NULL) { 
            
                printf("File cannot open! " );
                exit(0);                      
            }

            // 初始化要使用的数组
            
            fft_flag = 0;
            
            // int f1 = 100; 
            // int f2 = 200;
            // int f3 = 300;
            // for (i = 0; i < N; i++) {                       //生成输入信号

	        // 	t[i] = i * T;
	        // 	// pr[i] = 2 + 6 * sin(2 * PI * f1 * t[i] - PI / 6) + 0.02 * sin(2 * PI * f2 * t[i] + PI / 2) + 0.01 * sin(2 * PI * f3 * t[i] + PI / 3);
            //     pr[i] = 0.1*sin(2 * PI * f1 * t[i] - PI / 6) + 0.0001 * sin(2 * PI * f2 * t[i] + PI / 2) + 0.0001 * sin(2 * PI * f3 * t[i] + PI / 3);
            //     pi[i] = 0.0;
            //     fprintf(fp_sine,"%f\n", pr[i]);
            //     // printf("%d\t%f\n",i,pr[i]); //输出结果
            // }

            wavdata = (double *) calloc ( N, sizeof(double) );
            ret = parse_wave_file_double("sine_24bit_48k.wav", wavdata);
            if(ret != 0) {
                ERRO("parse_wave_file Error \n"); 
                break;
            }
            
            for(i = 0; i < N; i++) {
                pr[i] = wavdata[i];
                pi[i] = 0;
                // fprintf(fp_sine, "%.15f\n", pr[i]);
            }
            free(wavdata); 

            // 截断信号 48000 个
            double interp_x[Fs/2], interp_y[Fs/2], interp_spline_x[M/2], interp_spline_y[M/2];
            double interp_x2[Fs/2], interp_y2[Fs/2], interp_spline_x2[M/2], interp_spline_y2[M/2];

            for (i = 0; i < M/2; i++) {
		        interp_spline_x[i] = (double)(i*48000/65536.0);
                if(i < Fs/2) {
                    interp_x[i] = i;
                    interp_y[i] = pr[i];
                }
	        }
	        SPL(Fs/2, interp_x, interp_y, M/2, interp_spline_x, interp_spline_y);
            for (i = 0; i < M/2; i++) {
		        interp_spline_x2[i] = (double)(i*48000/65536.0);
                if(i < Fs/2) {
                    interp_x2[i] = i;
                    interp_y2[i] = pr[i + 48000/2];
                }
	        }
	        SPL(Fs/2, interp_x2, interp_y2, M/2, interp_spline_x2, interp_spline_y2);
            
            double interp_spline[N];
            memset(interp_spline, 0, sizeof(interp_spline));

            for(i = 0; i < M; i++) {

                if(i < M/2) {
                    interp_spline[i] = interp_spline_y[i];
                }else{
                    interp_spline[i] = interp_spline_y2[i - M/2];
                }

                fprintf(fp_sine, "%.15f\n", interp_spline[i]);        // 打印sine到txt
            }

            // FFT
            kfft(interp_spline, pi, M, Mn, fr, fi);                   //调用FFT函数 fft取样点M = 2^k
            
            double spl_fft_data[M];
	        for (i = 0; i < M; i++) { 
                fprintf(fp_fftdata, "%.15f\n", interp_spline[i]);      //打印FFT幅值到txt
                // printf("%d\t%f\n",i,pr[i]);                         //输出结果
                spl_fft_data[i] = interp_spline[i];
            }
            
            // 直流分量
            if(spl_fft_data[0] > spl_fft_data[1]) {
                direct_frequency = 0;
                direct_amplitude = spl_fft_data[0] / (M * 1.0);
            }

            z = 0;
            molecule = 0.0;
            denominator = 0.0;
            denominator_n = 0;
            thd = 0.0;
            temp = 0;

            // 找出频域中前1024个脉冲信号
            memset(fft_data_a, 0, sizeof(fft_data_a));
            memset(fft_data_n, 0, sizeof(fft_data_n));
            for(i = 1; i < (M/2 - 1); i++) {
                if(spl_fft_data[i] > 0.0001)
                    if( (spl_fft_data[i] > spl_fft_data[i - 1]) && (spl_fft_data[i] > spl_fft_data[i + 1]) ) {
                        fft_data_n[z] = i;
                        fft_data_a[z++] = spl_fft_data[i];
                        if(z >= 1024) {
                            break;
                        }   
                        i++;
                    }
            }

            // 冒泡法排序,目的找出基波信号
            int fft_len = (double) sizeof(fft_data_a) / sizeof(*fft_data_a);
            bubble_sort(fft_data_a, fft_data_n, fft_len);

            // 得到频域基波分量幅值
            denominator = fft_data_a[0] / (M / 2.0);                        // 基波分量 时域幅值

            // 频率分辨率
            double Fs_Resolution = 0.0;                                     // 频率分辨率
            // Fs_Resolution = Fs / (M * 1.0);
            Fs_Resolution = M / (M * 1.0);


            // 得到基波分量频率
            denominator_n = (int)(fft_data_n[0] * Fs_Resolution + 0.5);      // 基波分量 时域频率

            // 找出其他谐波分量
            int fn_n[30];                                                   // 存储谐波分量频率点
            memset(fn_n, 0, sizeof(fn_n));
            for(i = 0; i < 30; i++) {
                fn_n[i] = (denominator_n * i) / Fs_Resolution;
            }

            int count_n = 0;
            double fft_data[256];
            int fft_temp = 0;
            // double fft_buff_del;
            j = 2;
            memset(fft_data, 0, sizeof(fft_data));
            for(i = 0; i < 30; i++) {
                fft_temp = fn_n[j++];
                // fft_buff_del = pr[fft_temp];
                if( spl_fft_data[fft_temp] > spl_fft_data[fft_temp + 1] && spl_fft_data[fft_temp] > spl_fft_data[fft_temp - 1] ) {
                    fft_data[count_n++] = spl_fft_data[fft_temp];
                }

                if(j >= 30) {
                    break;
                }
            }
            
            // 计算THD分子
            for(i = 0; i < count_n; i++) {
                molecule = pow(fft_data[i] / (M / 2.0), 2) + molecule;
            }

            molecule = sqrt(molecule);                          // 各次谐波平方和开根

            thd = molecule / denominator;
            printf("THD is : %f(percentage)\n", thd);
            
            temp = thd * 100000000;
            
            //int数写入char数组
            // char *thd_char = (char *)&temp;
	        for (i = 0; i < 4; i++) {
		        thd_data[i] = (temp >> (8 * i)) & 0xff;
	        }

            tcp_send_qt(0x0a, thd_data, 4); 

            // 关闭文件
            fclose(fp_fftdata);
            fclose(fp_sine);
        }
    }

}


static int spline(int n, int end1, int end2,
				  double slope1, double slope2,
				  double x[], double y[],
				  double b[], double c[], double d[],
				  int *iflag)
{
	int nm1, ib, i, ascend;
	double t;
	nm1 = n - 1;
	*iflag = 0;
	if (n < 2) { /* no possible interpolation */
		*iflag = 1;
		goto LeaveSpline;
	}
	ascend = 1;
	for (i = 1; i < n; ++i) 
        if (x[i] <= x[i - 1]) 
            ascend = 0;
	
    if (!ascend) {
		*iflag = 2;
		goto LeaveSpline;
	}
	
    if (n >= 3) {
		
        d[0] = x[1] - x[0];
		c[1] = (y[1] - y[0]) / d[0];
		
        for (i = 1; i < nm1; ++i) {
			d[i] = x[i + 1] - x[i];
			b[i] = 2.0 * (d[i - 1] + d[i]);
			c[i + 1] = (y[i + 1] - y[i]) / d[i];
			c[i] = c[i + 1] - c[i];
		}
		/* ---- Default End conditions */
		b[0] = -d[0];
		b[nm1] = -d[n - 2];
		c[0] = 0.0;
		c[nm1] = 0.0;
		
        if (n != 3) {
			c[0] = c[2] / (x[3] - x[1]) - c[1] / (x[2] - x[0]);
			c[nm1] = c[n - 2] / (x[nm1] - x[n - 3]) - c[n - 3] / (x[n - 2] - x[n - 4]);
			c[0] = c[0] * d[0] * d[0] / (x[3] - x[0]);
			c[nm1] = -c[nm1] * d[n - 2] * d[n - 2] / (x[nm1] - x[n - 4]);
		}
		
        /* Alternative end conditions -- known slopes */
		if (end1 == 1) {
			b[0] = 2.0 * (x[1] - x[0]);
			c[0] = (y[1] - y[0]) / (x[1] - x[0]) - slope1;
		}
		if (end2 == 1) {
			b[nm1] = 2.0 * (x[nm1] - x[n - 2]);
			c[nm1] = slope2 - (y[nm1] - y[n - 2]) / (x[nm1] - x[n - 2]);
		}
		
        /* Forward elimination */
		for (i = 1; i < n; ++i) {
			t = d[i - 1] / b[i - 1];
			b[i] = b[i] - t * d[i - 1];
			c[i] = c[i] - t * c[i - 1];
		}
		
        /* Back substitution */
		c[nm1] = c[nm1] / b[nm1];
		for (ib = 0; ib < nm1; ++ib) {
			i = n - ib - 2;
			c[i] = (c[i] - d[i] * c[i + 1]) / b[i];
		}
		b[nm1] = (y[nm1] - y[n - 2]) / d[n - 2] + d[n - 2] * (c[n - 2] + 2.0 * c[nm1]);
		for (i = 0; i < nm1; ++i) {
			b[i] = (y[i + 1] - y[i]) / d[i] - d[i] * (c[i + 1] + 2.0 * c[i]);
			d[i] = (c[i + 1] - c[i]) / d[i];
			c[i] = 3.0 * c[i];
		}
		c[nm1] = 3.0 * c[nm1];
		d[nm1] = d[n - 2];
	}else{
		
        b[0] = (y[1] - y[0]) / (x[1] - x[0]);
		c[0] = 0.0;
		d[0] = 0.0;
		b[1] = b[0];
		c[1] = 0.0;
		d[1] = 0.0;
	}
LeaveSpline:
	return 0;
}
 
// n=48000 ni=65536 xi=插值后x  y=插值前y
static double seval(int ni, double u,
					int n, double x[], double y[],
					double b[], double c[], double d[],
					int *last)
{
	int i = 0, j = 0, k = 0;
	double w = 0.0;
	i = *last;
	if (i >= n - 1) 
        i = 0;
	if (i < 0) 
        i = 0;
	if ((x[i] > u) || (x[i + 1] < u)) {      //??
		i = 0;
		j = n;
		do {
			k = (i + j) / 2;
			if (u < x[k]) 
                j = k;
			if (u >= x[k]) 
                i = k;
		} while (j > i + 1);
	}
	*last = i;
	w = u - x[i];
	w = y[i] + w * (b[i] + w * (c[i] + w * d[i]));
	return (w);
}
 
 
void SPL(int n, double *x, double *y, int ni, double *xi, double *yi)
{
	double *b, *c, *d;
	int iflag = 0, last = 0, i = 0;
	b = (double *)malloc(sizeof(double) * n);
	c = (double *)malloc(sizeof(double) * n);
	d = (double *)malloc(sizeof(double) * n);
	if (!d) { 
        printf("no enough memory for b,c,d\n"); 
    }
	else {
        
		spline(n, 0, 0, 0, 0, x, y, b, c, d, &iflag);
		
        if (iflag == 0) 
			printf("I got coef b,c,d now\n"); 
		else 
			printf("x not in order or other error\n");

		for (i = 0; i < ni; i++) 
			yi[i] = seval(ni, xi[i], n, x, y, b, c, d, &last);
 
		free(b); 
		free(c); 
		free(d);
	}
}


/*
 * 冒泡法排序
 */
void bubble_sort(double arr[], int arr_n[], int len) 
{
    int i, j;
    double temp;
    int temp_n;

    for (i = 0; i < len - 1; i++)
        for (j = 0; j < len - 1 - i; j++)
            if (arr[j] < arr[j + 1]) {
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;

                temp_n = arr_n[j];
                arr_n[j] = arr_n[j + 1];
                arr_n[j + 1] = temp_n;
            }
}