【力扣】216. 组合总和 III <回溯、回溯剪枝>
【力扣】216. 组合总和 III
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
只使用数字 1 到 9,每个数字最多使用一次,返回所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。
示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在 [1,9] 范围内使用 4 个不同的数字,我们可以得到的最小和是 1+2+3+4 = 10,因为10 > 1,没有有效的组合。
提示:
2 <= k <= 9
1 <= n <= 60
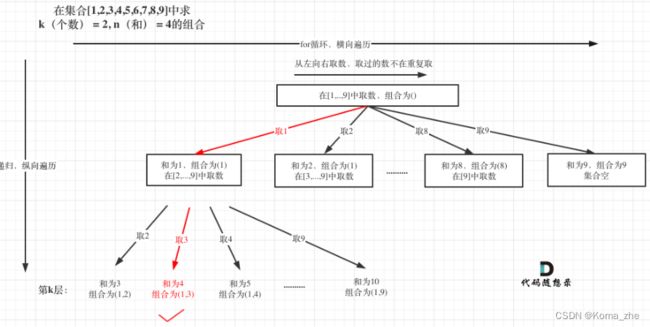
题解
import java.util.*;
class Solution {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
backTracking(n, k, 1, 0);
return result;
}
private void backTracking(int targetSum, int k, int startIndex, int sum) {
if (path.size() == k) {
if (sum == targetSum) {
result.add(new ArrayList<>(path));
}
return;
}
for (int i = startIndex; i <= 9 ; i++) {
path.add(i);
sum += i;
backTracking(targetSum, k, i + 1, sum);
//回溯
path.removeLast();
//回溯
sum -= i;
}
}
}
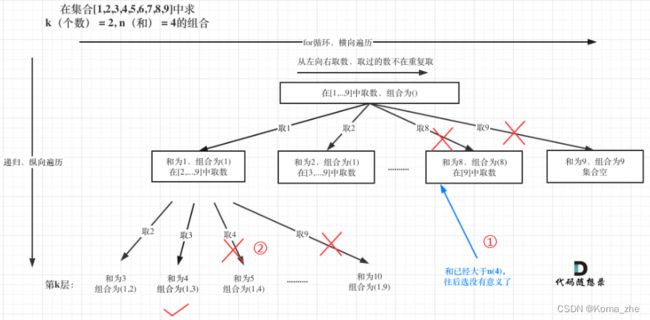
剪枝
import java.util.*;
class Solution {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
backTracking(n, k, 1, 0);
return result;
}
private void backTracking(int targetSum, int k, int startIndex, int sum) {
// 减枝
if (sum > targetSum) {
return;
}
if (path.size() == k) {
if (sum == targetSum) {
result.add(new ArrayList<>(path));
}
return;
}
// 减枝 9 - (k - path.size()) + 1
for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
path.add(i);
sum += i;
backTracking(targetSum, k, i + 1, sum);
//回溯
path.removeLast();
//回溯
sum -= i;
}
}
}