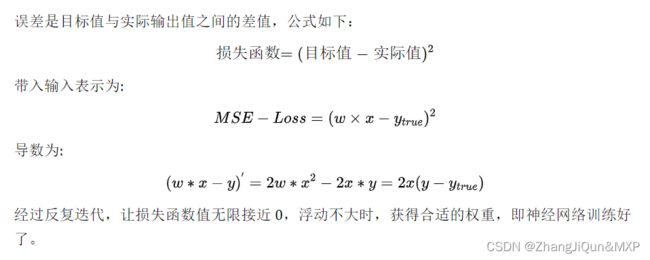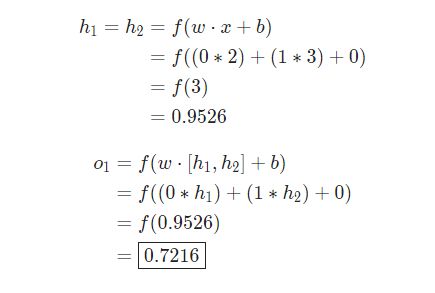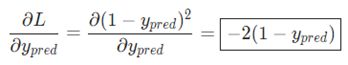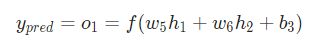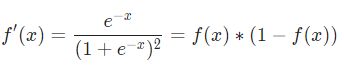神经网络的工作原理
目录
神经网络的介绍
神经网络的组成
神经网络的工作原理
Numpy 实现神经元
Numpy 实现前向传播
Numpy 实现一个可学习的神经网络
神经网络的介绍
神经网络受人类大脑启发的算法。简单来说,当你睁开眼睛时,你看到的物体叫做数据,再由你大脑中处理数据的 Nuerons(细胞)操作,识别出你所看到的物体,这是神经网络的工作过程。人工神经网络(Artificial Neural Network,ANN),它们不像你大脑中的神经元一样操作,而是模拟神经网络的性质和功能。
神经网络的组成
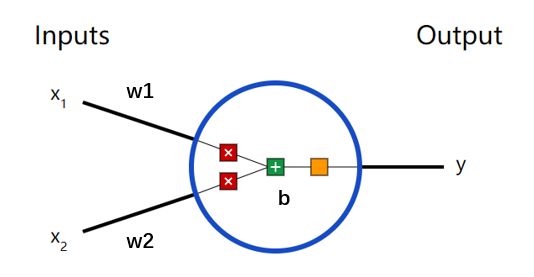
人工神经网络由大量高度相互关联的处理单元(神经元)协同工作来解决特定问题。首先介绍一种名为感知机的神经元。感知机接收若干个输入,每个输入对应一个权重值(可以看成常数),用它们做一些数学运算,然后产生一个输出。
接下来用形象化的例子解释感知机,假设有一个计划,周末去徒步,影响计划是否进行的因素有这些:
(1)周末是否加班;
(2)周末的天气是否恶劣;
(3)往返徒步地点是否方便;
对于不同人,三个因素的影响效果也不一样,如果 输入(2)对于你来说影响非常大,这样就设置的权重值就大,反之权重值就小。
再将输入二值化,对于天气不恶劣,设置为 1(),对于天气恶劣,设置为 0(),天气的影响程度通过权重值体现,设置为 10()。同样设置输入(1)的权值为 8(),输入(3)的权重值为 1()。输出二值化是去徒步为 1(),不去为 0()。
假设对于感知机,如果 的结果大于某阈值(如 5),表示去徒步 ,随机调整权重,感知机的结果会不一样。
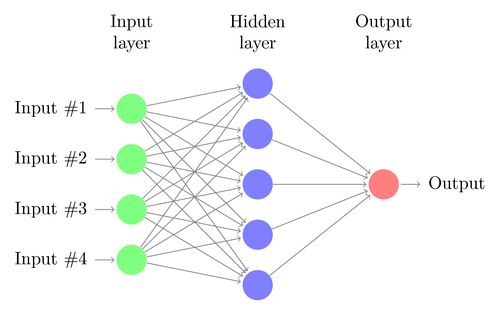
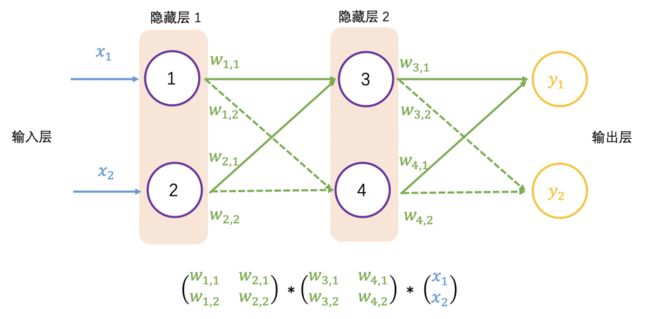
一个典型的神经网络有成百上千个神经元(感知机),排成一列的神经元也称为单元或是层,每一列的神经元会连接左右两边的神经元。感知机有输入和输出,对于神经网络是有输入单元与输出单元,在输入单元和输出单元之间是一层或多层称为隐藏单元。一个单元和另一个单元之间的联系用权重表示,权重可以是正数(如一个单元激发另一个单元) ,也可以是负数(如一个单元抑制或抑制另一个单元)。权重越高,一个单位对另一个单位的影响就越大。
神经网络的工作原理
神经网络的工作大致可分为前向传播和反向传播,类比人们学习的过程,
前向传播如读书期间,学生认真学习知识点,进行考试,获得自己对知识点的掌握程度;
反向传播是学生获得考试成绩作为反馈,调整学习的侧重点。
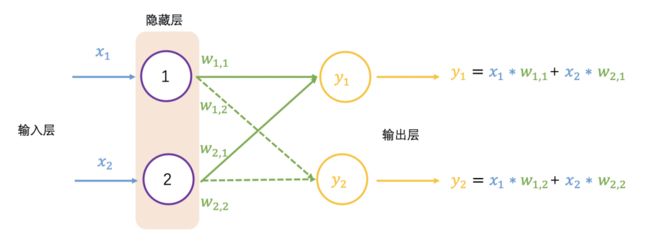
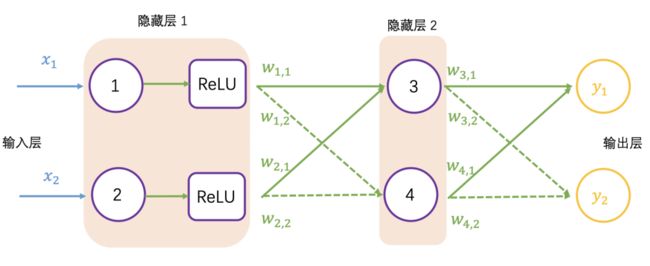
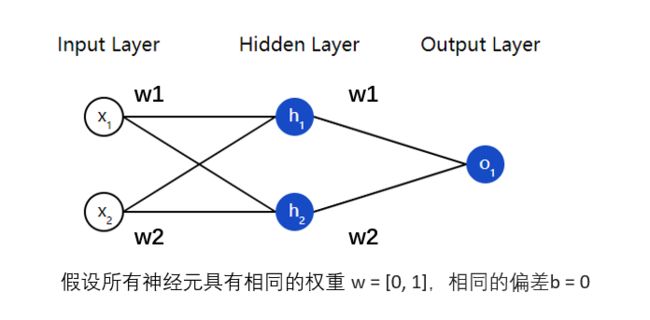
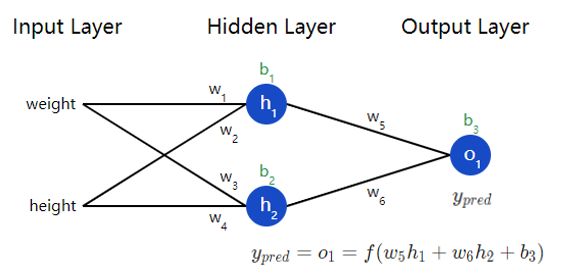
以下展示了 2 个输入和 2 个输出的神经网络:
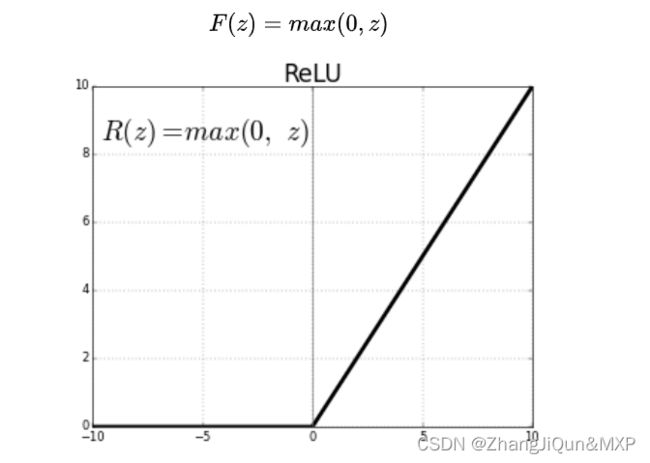
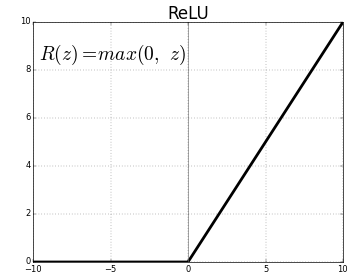
大多数真实世界的数据是非线性的,我们希望神经元学习这些非线性表示,可以通过激活函数将非线性引入神经元。例如徒步例子中的阈值,激活函数 ReLU(Rectified Linear Activation Function)的阈值为 0,对于大于 0 的输入,输出为输入值,对于小于 0 的输入值,输出为 0,公式和图像表示如下:
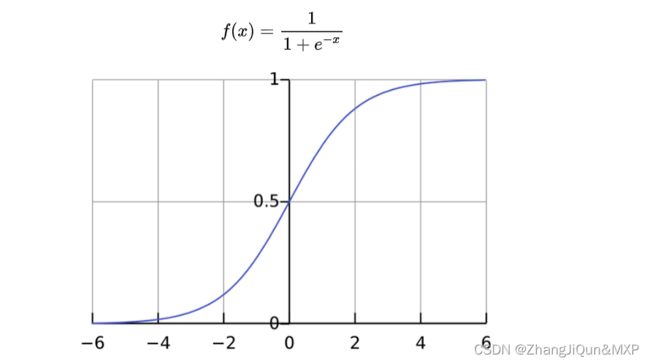
这里扩展一下,激活函数有很多种,例如常用的 sigmoid 激活函数,只输出范围内的数字 ,它将无界输入转换为具有良好、可预测的输出形式,sigmoid 函数的公式和图像如下。
加入 ReLU 激活函数的神经网络如下图所示:
加入 SoftMax 函数的神经网络如下图所示:
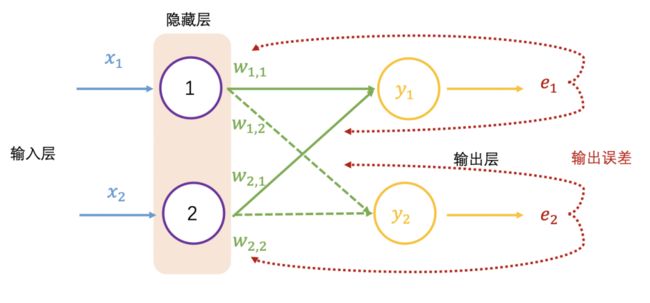
获得神经网络的输出值 (0.98, 0.02) 之后,与真实值 (1, 0) 比较,非常接近,仍然需要与真实值比较,计算差距(也称误差,用 e表示),就跟摸底考试一样,查看学习的掌握程度,同样神经网络也要学习,让输出结果无限接近真实值,也就需要调整权重值,这里就需要反向传播了。
在反向传播过程中需要依据误差值来调整权重值,可以看成参数优化过程,简要过程是,先初始化权重值,再增加或减少权重值,查看误差是否最小,变小继续上一步相同操作,变大则上一步相反操作,调整权重后查看误差值,直至误差值变小且浮动不大。
斜率的大小表明变化的速率,意思是当斜率比较大的情况下,权重 变化所引起的结果变化也大。把这个概念引入求最小化的问题上,以权重导数乘以一个系数作为权重更新的数值,这个系数我们叫它学习率(learning rate),这个系数能在一定程度上控制权重自我更新,权重改变的方向与梯度方向相反,如下图所示,权重的更新公式如下:
import numpy as np
def mse-loss(y_true, y_pred):
# y_true and y_pred are numpy arrays of the same length.
return ((y_true - y_pred) ** 2).mean()
y_true = np.array([1, 0, 0, 1])
y_pred = np.array([0, 0, 0, 0])
print(mse_loss(y_true, y_pred)) # 0.5
Numpy 实现神经元
以上介绍了神经网络的基本结构及数学原理,为了方便大家理解,参数围绕着 ,后续继续深入学习,便遇到 参数(称为偏差),神经元会有以下这样的形式。
Python 代码实现如下:
import numpy as np
def sigmoid(x):
# Our activation function: f(x) = 1 / (1 + e^(-x))
return 1 / (1 + np.exp(-x))
class Neuron:
def __init__(self, weights, bias):
self.weights = weights
self.bias = bias
def feedforward(self, inputs):
# Weight inputs, add bias, then use the activation function
total = np.dot(self.weights, inputs) + self.bias
return sigmoid(total)
weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4 # b = 4
n = Neuron(weights, bias)
x = np.array([2, 3]) # x1 = 2, x2 = 3
print(n.feedforward(x)) # 0.9990889488055994
Numpy 实现前向传播
同样在神经网络中,如下图所示,这个网络有 2 个输入,一个隐藏层有 2 个神经元( 和 ),和一个有 1 个神经元的输出层()。
Python 代码实现如下:
import numpy as np
class OurNeuralNetwork:
'''
A neural network with:
- 2 inputs
- a hidden layer with 2 neurons (h1, h2)
- an output layer with 1 neuron (o1)
Each neuron has the same weights and bias:
- w = [0, 1]
- b = 0
'''
def __init__(self):
weights = np.array([0, 1])
bias = 0
# The Neuron class here is from the previous section
self.h1 = Neuron(weights, bias)
self.h2 = Neuron(weights, bias)
self.o1 = Neuron(weights, bias)
def feedforward(self, x):
out_h1 = self.h1.feedforward(x)
out_h2 = self.h2.feedforward(x)
# The inputs for o1 are the outputs from h1 and h2
out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))
return out_o1
network = OurNeuralNetwork()
x = np.array([2, 3])
print(network.feedforward(x)) # 0.7216325609518421
Numpy 实现一个可学习的神经网络
终于到了实现一个完整的神经网络的时候了,把参数全安排上,别吓着了~
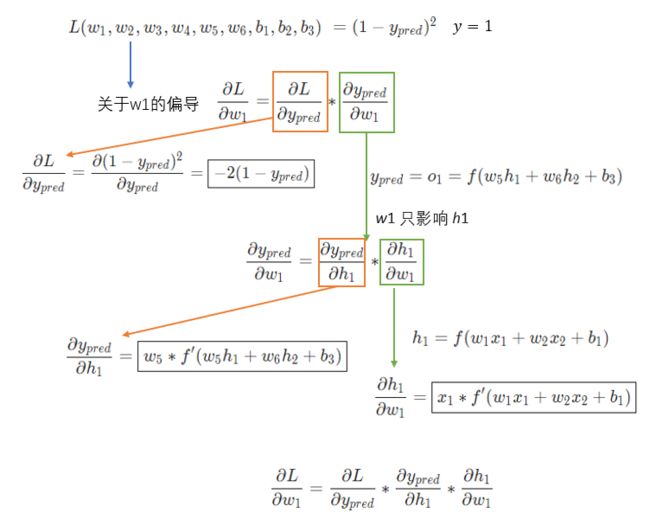
现在有一个明确的目标:最小化神经网络的损,将损失写成多变量函数,其中 。
变量多的时候,求其中一个变量的导数时,成为求偏导数,接下来求 的偏导数,公式如下:
橙色框的内容关于损失函数可以直接得到:
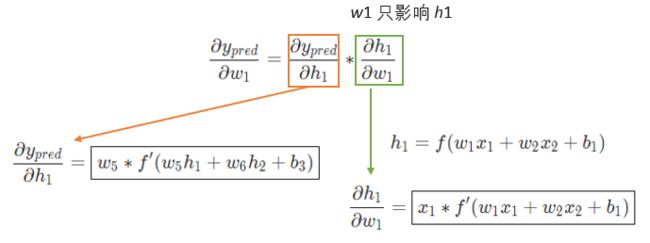
绿色框的内容,继续分析 :
只影响 不影响 ,绿色框的内容拆解为:
最终关于 的偏导数,公式如下:
为了便于大家理解,将公式放在一起,请查阅~
这里会对 sigmoid 函数求导,求导的结果如下:
获得偏导数后,回忆一下参数的更新公式:
学习率偏导数
-
如果偏导数为正,则参数减少;
-
如果偏导数为负,则参数增加。
如果我们对网络中的每个权重和偏差都这样做,损失将慢慢减少。
整个过程如下:
-
1.从我们的数据集中选择一个样本,进行操作
-
2.计算损失中关于权重和偏差的偏导数
-
3.使用更新公式更新每个权重和偏差
-
4.回到步骤1