Java学数据结构(3)——树Tree & B树 & 红黑树 & Java标准库中的集合Set与映射Map & 使用多个映射Map的案例
目录
- 引出
- B树
-
- 插入insert
- 删除remove
- 红黑树(red black tree)
-
- 自底向上的插入
- 自顶向下红黑树
- 自顶向下的删除
- 标准库中的集合Set与映射Map
-
- 关于Set接口
- 关于Map接口
- TreeSet类和TreeMap类的实现
- 使用多个映射Map:一个词典的案例
-
- 方案一:使用一个Map对象
- 方案二:按照长度分组
- 方案三:按照多个字母分组
- 原书代码
- 总结
引出
1.B树,阶M,数据树叶上,根的儿子数在2和M之间,除根外,非树叶节点儿子为M/2和M之间;
2.B树的插入引起分裂,B树的删除,引起合并和领养;
3.红黑树,根是黑的,红色节点的儿子必须是黑的,所有路径的黑色节点数相同;
4.红黑树的插入,颜色翻转,单旋转,插入节点定颜色;
5.java标准库的set和map,使用红黑树;
B树
迄今为止,我们始终假设可以把整个数据结构存储到计算机的主存中。可是,如果数据更多装不下主存,那么这就意味着必须把数据结构放到磁盘上。此时,因为大O模型不再适用,所以导致游戏规则发生了变化。
在磁盘上,典型的查找树执行如下:设想要访问佛罗里达州公民的驾驶记录。假设有1千万项,每一个关键字是32字节(代表一个名字),而一个记录是256个字节。假设这些数据不能都装人主存,而我们是正在使用系统的20个用户中的一个(因此有1/20的资源)。这样,在1秒内,我们可以执行2500万次指令,或者执行6次磁盘访问。
不平衡的二叉查找树是一个灾难。在最坏情形下它具有线性的深度,从而可能需要1千万次磁盘访问。平均来看,一次成功的查找可能需要1.381ogN次磁盘访问,由于10g10000000≈24,因此平均一次查找需要32次磁盘访问,或5秒的时间。在一棵典型的随机构造的树中,我们预料会有一些节点的深度要深3倍;它们需要大约100次磁盘访问,或16秒的时间。
AVL树多少要好一些。1.44logN的最坏情形不可能发生,典型的情形是非常接近于logN。这样,一棵AVL树平均将使用大约25次磁盘访问,需要的时间是4秒。
我们想要把磁盘访问次数减小到一个非常小的常数,比如3或4:而且我们愿意写一个复杂的程序来做这件事,因为在合理情况下机器指令基本上是不占时间的。由于典型的AVL树接近到最优的高度,因此应该清楚的是,二叉查找树是不可行的。使用二叉查找树我们不能行进到低于logN。解法直觉上看是简单的:如果有更多的分支,那么就有更少的高度
。这样,31个节点的理想二叉树(perfect binary tree)有5层,而31个节点的5叉树则只有3层,如图4-59所示一棵M叉查找树(M-ary search tree)可以有M路分支。随着分支增加,树的深度在减少。一棵完全二叉树(complete binary tree)的高度大约为logN,而一棵完全M叉树(complete M-ary tree) 的高度大约是logm N。
我们可以以与建立二叉查找树大致相同的方式建立M叉查找树。在二叉查找树中,需要一个关键字来决定两个分支到底取用哪个分支;而在M叉查找树中需要M1个关键字来决定选取哪个分支。为使这种方案在最坏的情形下有效,需要保证M叉查找树以某种方式得到平衡。否则,像二叉查找树,它可能退化成一个链表。实际上,我们甚至想要更加限制性的平衡条件,即
不想要M叉查找树退化到甚至是二叉查找树,因为那时我们又将无法摆脱logN次访问了。
B+树、B树
图4-60显示5阶B树的一个例子。注意,所有的非叶节点的儿子数都在3和5之间(从而有2到4个关键字);根可能只有两个儿子。这里,我们有L=5(在这个例子中L和M恰好是相同的,但这不是必需的)。由于L是5,因此每片树叶有3到5个数据项。要求节点半满将保证B树不致退化成简单的二叉树。虽然存在改变该结构的各种B树的定义,但大部分在一些次要的细节上变化,而我们这个定义是流行的形式之一。
插入insert
我们首先考查插入。设想要把57插人到图4-60的B树中。沿树向下查找揭示出它不在树中。此时我们把它作为第5项添加到树叶中。注意我们可能要为此重新组织该树叶上的所有数据。然而,与磁盘访问相比(在这种情况下它还包含一次磁盘写),这项操作的开销可以忽略不计。
当然,这是相对简单的,因为该树叶还没有被装满。设现在要插入55。图4-61显示一个问题:55想要插入其中的那片树叶已经满了。不过解法却不复杂:由于我们现在有L+1项,因此把它们分成两片树叶,这两片树叶保证都有所需要的记录的最小个数。我们形成两片树叶,每叶3项。写这两片树叶需要2次磁盘访问,更新它们的父节点需要第3次磁盘访问。注意,在父节点中关键字和分支均发生了变化,但是这种变化是以容易计算的受控的方式处理的。最后得到的B树在图4-62中给出。虽然分裂节点是耗时的,因为它至少需要2次附加的磁盘写,但它相对很少发生。
例如,如果L是32,那么当节点被分裂时,具有16和17项的两片树叶分别被建立。对于有17项的那片树叶,我们可以再执行15次插入而不用另外的分裂。换句话说,对于每次分裂,大致存在L/2次非分裂的插人。
前面例子中的节点分裂之所以行得通是因为其父节点的儿子个数尚未满员。可是,如果满员了又会怎样呢?例如,假设我们想要把40插入到图4-62的B树中。此时必须把包含关键字35到39而现在又要包含40的树叶分裂成2片树叶。但是这将使父节点有6个儿子,可是它只能有5个儿子。因此,解法就要分裂这个父节点。结果在图4-63中给出。当父节点被分裂时,必须更新那些关键字以及还有父节点的父亲的值,这样就招致额外的两次磁盘写(从而这次插入花费5次磁盘写)。然而,虽然由于有大量的情况要考虑而使得程序确实不那么简单,但是这些关键字还是以受控的方式变化。
正如这里的情形所示,当一个非叶节点分裂时,它的父节点得到了一个儿子。如果父节点的儿子个数已经达到规定的限度怎么办呢?在这种情况下,继续沿树向上分裂节点直到找到一个不需要再分裂的父节点,或者到达树根。
如果分裂树根,那么我们就得到两个树根。显然这是不可接受的,但我们可以建立一个新的根,这个根以分裂得到的两个树根作为它的两个儿子。
这就是为什么准许树根可以最少有两个儿子的特权的原因。这也是B树增加高度的唯一方式。不用说,一路向上分裂直到根的情况是一种特别少见的异常事件,因为一棵具有4层的树意味着在整个插入序列中已经被分裂了3次(假设没有删除发生)。
事实上,任何非叶节点的分裂也是相当少见的。还有其他一些方法处理儿子过多的情况。一种方法是在相邻节点有空间时把一个儿子交给该邻节点领养。例如,为了把29插入到图4-63的B树中,可以把32移到下一片树叶而腾出一个空间。这种方法要求对父节点进行修改,因为有些关键字受到了影响。然而,它趋向于使得节点更满,从而在长时间运行中节省空间。
删除remove
我们可以通过查找要删除的项并在找到后删除它来执行删除操作。
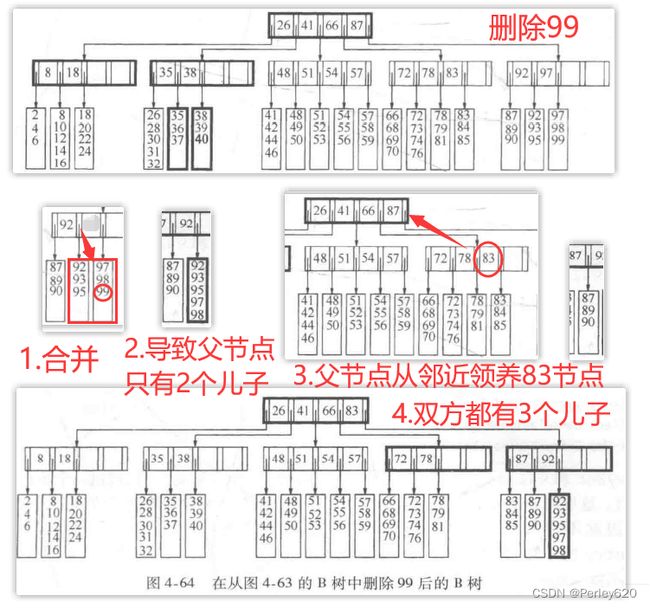
问题在于,如果被删元所在的树叶的数据项数已经是最小值,那么删除后它的项数就低于最小值了。我们可以通过在邻节点本身没有达到最小值时领养一个邻项来矫正这种状况。如果相邻结点已经达到最小值,那么可以与该相邻节点联合以形成一片满叶。可是,这意味着其父节点失去一个儿子。如果失去儿子的结果又引起父节点的儿子数低于最小值,那么我们使用相同的策略继续进行。这个过程可以一直上行到根。根不可能只有一个儿子(要是允许根有一个儿子那可就愚蠢了)。如果这个领养过程的结果使得根只剩下一个儿子,那么删除该根并让它的这个儿子作为树的新根。这是B树降低高度的唯一的方式。
例如,假设我们想要从图4-63的B树中删除99。由于那片树叶只有两项而它的邻居已经是最小值3项了,因此我们把这些项合并成有5项的一片新的树叶。结果,它们的父节点只有两个儿子了。这时该父节点可以从它的邻节点领养,因为邻节点有4个儿子。领养的结果使得双方都有3个儿子,结果如图4-64所示。
红黑树(red black tree)
历史上AVL树流行的另一变种是红黑树(red black tree)。对红黑树的操作在最坏情形下花费O(logN)时间,而且我们将看到,(对于插入操作的)一种审慎的非递归实现可以相对容易地完成(与AVL树相比)。
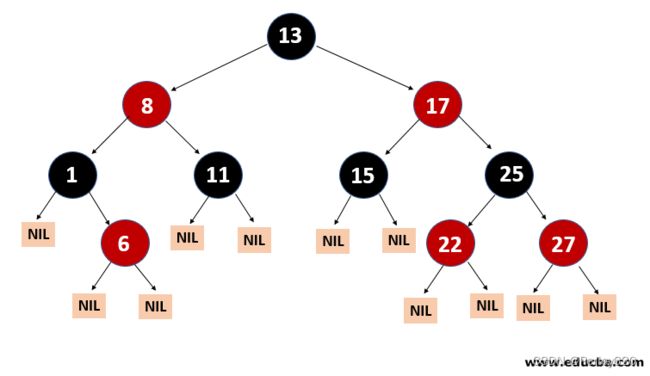
红黑树是具有下列着色性质的二叉查找树:
1.每一个节点或者着成红色,或者着成黑色。
2.根是黑色的。
3.如果一个节点是红色的,那么它的子节点必须是黑色的。
4.从一个节点到一个null引用的每一条路径必须包含相同数目的黑色节点。
着色法则的一个结论是,红黑树的高度最多是2log(N+1)。因此,查找操作保证是一种对数的操作。
自底向上的插入
前面已经提到,如果新插入的项的父节点是黑色,那么插入完成。因此,将25插入到图12-9的树中是简单的操作。
如果父节点是红色的,那么有几种情形(每种都有一个镜像对称)需要考虑。首先,假设这个父节点的兄弟是黑色的(我们采纳约定:u11节点都是黑色的)。这对于插人3或8是适用的,但对插入99不适用。令X是新添加的树叶,P是它的父节点,S是该父节点的兄弟(若存在),G是祖父节点。在这种情形只有X和P是红色的,G是黑色的,否则就会在插入前有两个相连的红色节点,违反了红黑树的法则。采用伸展树的术语,X,P和G可以形成一个一字形链或之字形链(两个方向中的任一个方向)。
图12-10指出当P是一个左儿子时(注意有一个对称情形)我们应该如何旋转该树。即使X是一片树叶,我们还是画出较一殷的情形,使得X在树的中间。后面我们将用到这个较一般的旋转。
自顶向下红黑树
上滤的实现需要用一个栈或用一些父链保存路径。我们看到,如果使用一个自顶向下的过程,则伸展树会更有效,事实上我们可以对红黑树应用自顶向下的过程而保证S不会是红色的。
这个过程在概念上是容易的。在向下的过程中当看到一个节点X有两个红儿子的时候,可使X呈红色而让它的两个儿子是黑的。(如果X是根,则在颜色翻转后它将是红色,但是为恢复性质2可以直接着成黑色)
图12-11显示这种颜色翻转的现象,只有当X的父节点P也是红的时候这种翻转将破坏红黑的法则。但是此时可以应用图12-10中适当的旋转。如果X的父节点的兄弟是红色会如何呢?这种可能已经被从顶向下过程中的行动所排除,因此X的父节点的兄弟不可能是红色!
特别地,如果在沿树向下的过程中我们看到一个节点Y有两个红儿子,那么我们知道Y的孙子必然是黑的,由于Y的儿子也要变成黑的,甚至在可能发生的旋转之后,因此我们将不会看到两层上另外的红节点。这样,当我们看到X,若X的父节点是红的,则X的父节点的兄弟不可能也是红色的。
例如,假设要将45插入到图12-9中的树上。在沿树向下的过程中,我们看到50有两个红儿子。因此,我们执行一次颜色翻转,使50为红的,40和55是黑的。现在50和60都是红的。在60和70之间执行单旋转,使得60是30的右子树的黑根,而70和50都是红的。如果我们在路径上看到另外的含有两个红儿子的节点,那么我们继续执行同样的操作。当我们到达树叶时,把45作为红节点插入,由于父节点是黑的,因此插入完成。最后得到如图12-12所示的树。
如图12-12所示,所得到的红黑树常常平衡得很好。经验指出,平均红黑树大约和平均AVL树一样深,从而查找时间一般接近最优。红黑树的优点是执行插入所需要的开销相对较低,另外就是实践中发生的旋转相对较少。
自顶向下的删除
红黑树中的删除也可以自顶向下进行。每一件工作都归结于能够删除树叶。这是因为,要删除一个带有两个儿子的节点,用右子树上的最小节点代替它;该节点必然最多有一个儿子,然后将该节点删除。只有一个右儿子的节点可以用相同的方式删除,而只有一个左儿子的节点通过用其左子树上最大节点替换而被删除,然后再将该节点删除。注意,对于红黑树,我们不要使用绕过带有一个儿子的节点的情形的方法,因为这可能在树的中部连接两个红色节点,增加红黑条件实现的困难。
当然,红色树叶的删除很简单。然而,如果一片树叶是黑的,那么删除操作会复杂得多,因为黑色节点的删除将破坏条件4。解决方法是保证从上到下删除期间树叶是红的。在整个讨论中,令X为当前节点,T是它的兄弟,而P是它们的父亲。开始时我们把树的根涂成红色。当沿树向下遍历时,我们设法保证X是红色的。当到达一个新的节点时,我们要确信P是红的(归纳地,我们试图继续保持这种不变性)并且X和T是黑的(因为不能有两个相连的红色节点)。这存在两种主要的情形。首先,设X有两个黑儿子。
此时有三种子情况,如图12-17所示。如果T也有两个黑儿子,那么可以翻转X、T和P的颜色来保持这种不变性。否则,T的儿子之一是红的。根据这个儿子节点是哪一个,我们可以应用图12-17所示的第二和第三种情形表示的旋转。特别要注意,这种情形对于树叶将是适用的,因为nul1Node被认为是黑的。
其次,X的儿子之一是红的。在这种情形下,我们落到下一层上,得到新的X、T和P。如果幸运,X落在红儿子上,则我们可以继续向前进行。如果不是这样,那么我们知道T将是红的,而X和P将是黑的。我们可以旋转T和P,使得X的新父亲是红的;当然X及其祖父将是黑的。'此时我们可以回到第一种主情况。
标准库中的集合Set与映射Map
List容器即ArrayList和LinkedList用于查找效率很低。因此,Collections API提供了两个附加容器Set和Map,它们对诸如插入、删除和查找等基本操作提供有效的实现。
关于Set接口
Set接口代表不允许重复元的Collection。由接口SortedSet给出的一种特殊类型的Set保证其中的各项处于有序的状态。因为一个Set IS-A Collection,所以用于访问继承Collection的list的项的方法也对Set有效。
由Set所要求的一些独特的操作是一些插入、删除以及(有效地)执行基本查找的能力。对于Set,add方法如果执行成功则返回true,否则返回false,因为被添加的项已经存在。保持各项以有序状态的Set的实现是TreeSet。TreeSet类的基本操作花费对数最坏情形时间。
关于Map接口
Map是一个接口,代表由关键字以及它们的值组成的一些项的集合。关键字必须是唯一的,但是若干关键字可以映射到一些相同的值。因此,值不必是唯一的。在SortedMap接口中,映射中的关键字保持逻辑上有序状态。SortedMap接口的一种实现是TreeMap类。Map的基本操作包括诸如isEmpty、clear、size等方法,而且最重要的是包含下列方法:
get返回Map中与key相关的值,或当key不存在时返回null。如果在Map中不存在null值,那么由get返回的值可以用来确定key是否在Map中。然而,如果存在nul1值,那么必须使用containsKey。方法put把关键字/值对置入Map中,或者返回null,或者返回与key相联系的老值。
通过一个Map进行迭代要比Collection复杂,因为Map不提供迭代器,而是提供3种方法,将Map对象的视图作为Collection对象返回。由于这些视图本身就是Collection,因此它们可以被迭代。所提供的3种方法如下:
方法keySet和values返回简单的集合(这些关键字不包含重复元,因此以一个Set对象的形式返回)。这里的entrySet方法是作为一些项而形成的Set对象被返回的(由于关键字是唯一的,因此不存在重复项)。每一项均由被嵌套的接口Map.Entry表示。对于类型Map.Entry的对象,其现有的方法包括访问关键字、关键字的值,以及改变关键字的值:
TreeSet类和TreeMap类的实现
Java要求TreeSet和TreeMap支持基本的add、remove和contains操作以对数最坏情形时间完成。因此,基本的实现方法就是平衡二叉查找树。一般说来,我们并不使用AVL树,而是经常使用一些自顶向下的红黑树。
实现TreeSet和TreeMap的一个重要问题是提供对迭代器类的支持。当然,在内部,迭代器保留到迭代中“当前”节点的一个链接。困难部分是到下一个节点高效的推进。存在几种可能的解决方案,其中的一些方案叙述如下:
1.在构造迭代器时,让每个迭代器把包含诸TreeSet项的数组作为该迭代器的数据存储。这有不足,因为我们还可以使用toArray,并不需要迭代器。
2.让迭代器保留存储通向当前节点的路径上的节点的一个栈。根据该信息,可以推出迭代器中的下一个节点,它或者是包含最小项的当前节点右子树上的节点,或者包含其左子树当前节点的最近的祖先。这使得迭代器多少有些大,并导致迭代器的代码臃肿。
3.让查找树中的每个节点除存储子节点外还要存储它的父节点。此时迭代器不至于那么大,但是在每个节点上需要额外的内存,并且迭代器的代码仍然臃肿。
4.让每个节点保留两个附加的链:一个通向下一个更小的节点,另一个通向下一个更大的节点。这要占用空间,不过迭代器做起来非常简单,并且保留这些链也很容易。
5.只对那些具有nu11左链或nul1右链的节点保留附加的链。通过使用附加的布尔变量使得这些例程判断是一个左链正在被用作标准的二叉树左链还是一个通向下一个更小节点的链,类似地,对右链也有类似的判断。这种做法叫作线索树(threaded tree),用于许多平衡二叉查找树的实现中。
使用多个映射Map:一个词典的案例
许多单词都和另外一些单词相似。例如,通过改变第1个字母,单词wine可以变成dine、fine、line、mine、nine、pine或vine通过改变第3个字母,wine可以变成wide、wife、wipe或wire。通过改变第4个字母wine可以变成wind、wing、wink或wins。这样我们就得到l5个不同的单词,它们仅仅通过改变wine中的一个字母而得到。实际上,存在20多个不同的单词,其中有些单词更生僻。我们想要编写一个程序以找出通过单个字母的替换可以变成至少15个其他单词的单词。
假设我们有一个词典,由大约89000个不同长度的不同单词组成。大部分单词在6~11个字母之间。其中6字母单词有8205个,7字母单词有11989个,8字母单词13672个,9字母单词13014个,10字母单词11297个,11字母单词8617个(实际上,最可变化的单词是3字母、4字母和5字母单词,不过,更长的单词检查起来更耗费时间)。
方案一:使用一个Map对象
最直接了当的策略是使用一个Map对象,其中的关键字是单词,而关键字的值是用1字母替换能够从关键字变换得到的一列单词。
该算法的问题在于速度慢,在我们的计算机上花费75秒的时间。一个明显的改进是避免比较不同长度的单词。我们可以把单词按照长度分组,然后对各个分组运行刚才提供的程序。为此,可以使用第2个映射!此时的关键字是个整数,代表单词的长,而值则是该长度的所有单词的集合。我们可以使用一个List存储每个集合,然后应用相同的做法。程序所示。第9行是第2个Map的声明,第13行和第14行将分组置入该Map,然后用一个附加的循环对每组单词迭代。与第1个算法比较,第2个算法只是在边际上编程困难,其运行时间为16秒,大约快了5倍。
package com.tianju.book.jpa.mapLearn;
import java.io.BufferedReader;
import java.io.IOException;
import java.util.*;
public class WordDemo {
private static List<String> wordList = Arrays.asList(
"wine", "dine", "fine", "line", "mine", "nine", "pine", "vine", "wide",
"wife", "wipe", "wire", "wind", "wing", "wink", "wins");
/**
* 当两个单词长度相等,并且只有1个字母不同时返回true
*/
private static boolean isOneCharDiff(String word1,String word2){
if (word2.length()!=word1.length()){
return false; // 长度不同,返回false
}
int diff = 0;
for (int i=0;i<word1.length();i++){
if (word1.charAt(i)!=word2.charAt(i)){
if (diff>1){
return false;
}
diff = diff +1;
}
}
return diff == 1;
}
// {mine=[wine, dine, fine, line, nine, pine, vine], wins=[wine, wind, wing, wink],
/**
* 自己实现的方式,比大佬的要多一半的循环次数
* getAdjWords方法的for循环次数:96
* computeAdjacentWordsSlow方法的for循环次数:48
* @param words
* @return
*/
public static Map<String,List<String>> getAdjWords(List<String> words){
Map<String,List<String>> adjMap = new HashMap<>();
int forTimes = 0;
for (int i=0;i<words.size();i++){
for (int j=0;j<words.size();j++){
// System.out.println(words.get(i) + "--" + words.get(j));
if (isOneCharDiff(words.get(i), words.get(j))){ // 只有一个单词不同
List<String> stringList = adjMap.get(words.get(i));
if (stringList==null){
stringList = new ArrayList<>();
adjMap.put(words.get(i),stringList);
}
stringList.add(words.get(j));
forTimes++;
}
}
}
System.out.println("getAdjWords方法的for循环次数:"+forTimes);
return adjMap;
}
// Computes a map in which the keys are words and values are Lists of words
// that differ in only one character from the corresponding key.
// Uses a quadratic algorithm (with appropriate Map).
public static Map<String,List<String>> computeAdjacentWordsSlow( List<String> theWords )
{
Map<String,List<String>> adjWords = new HashMap<>( );
String [ ] words = new String[ theWords.size( ) ];
int forTimes = 0;
theWords.toArray( words );
for( int i = 0; i < words.length; i++ )
for( int j = i + 1; j < words.length; j++ )
if( isOneCharDiff( words[ i ], words[ j ] ) )
{
update( adjWords, words[ i ], words[ j ] );
update( adjWords, words[ j ], words[ i ] );
forTimes++;
}
System.out.println("computeAdjacentWordsSlow方法的for循环次数:"+forTimes);
return adjWords;
}
private static <KeyType> void update( Map<KeyType,List<String>> m, KeyType key, String value )
{
List<String> lst = m.get( key );
if( lst == null )
{
lst = new ArrayList<>( );
m.put( key, lst );
}
lst.add( value );
}
public static void main(String[] args) {
/**
* 第一种方式,把单词作为键,把只需要变换1个单词就能得到新单词的所有单词的List作为该键的值
*/
System.out.println(isOneCharDiff("dog", "dop"));
Map<String, List<String>> adjWords = getAdjWords(wordList);
System.out.println(adjWords);
Map<String, List<String>> listMap = computeAdjacentWordsSlow(wordList);
System.out.println(listMap);
}
}
方案二:按照长度分组
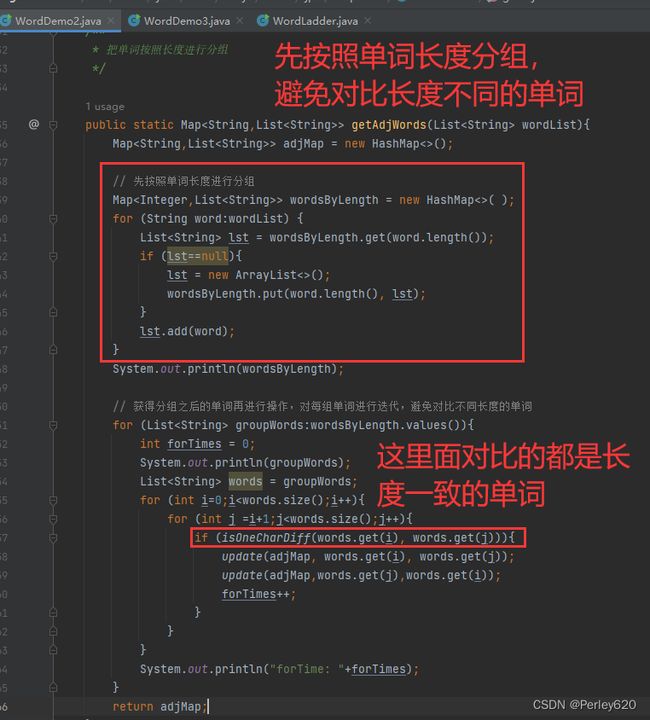
一个明显的改进是避免比较不同长度的单词。我们可以把单词按照长度分组,然后对各个分组运行刚才提供的程序。为此,可以使用第2个映射!此时的关键字是个整数,代表单词的长,而值则是该长度的所有单词的集合。我们可以使用一个List存储每个集合,然后应用相同的做法。程序所示。第9行是第2个Map的声明,第13行和第14行将分组置入该Map,然后用一个附加的循环对每组单词迭代。与第1个算法比较,第2个算法只是在边际上编程困难,其运行时间为16秒,大约快了5倍。
package com.tianju.book.jpa.mapLearn;
import java.util.*;
public class WordDemo2 {
private static List<String> wordList = Arrays.asList(
"wine", "dine", "fine", "line", "mine", "nine", "pine", "vine", "wide",
"wife", "wipe", "wire", "wind", "wing", "wink", "wins");
/**
* 当两个单词长度相等,并且只有1个字母不同时返回true
*/
private static boolean isOneCharDiff(String word1,String word2){
if (word2.length()!=word1.length()){
return false; // 长度不同,返回false
}
int diff = 0;
for (int i=0;i<word1.length();i++){
if (word1.charAt(i)!=word2.charAt(i)){
if (diff>1){
return false;
}
diff = diff +1;
}
}
return diff == 1;
}
/**
* 把单词按照长度进行分组
*/
public static Map<String,List<String>> getAdjWords(List<String> wordList){
Map<String,List<String>> adjMap = new HashMap<>();
// 先按照单词长度进行分组
Map<Integer,List<String>> wordsByLength = new HashMap<>( );
for (String word:wordList) {
List<String> lst = wordsByLength.get(word.length());
if (lst==null){
lst = new ArrayList<>();
wordsByLength.put(word.length(), lst);
}
lst.add(word);
}
System.out.println(wordsByLength);
// 获得分组之后的单词再进行操作,对每组单词进行迭代,避免对比不同长度的单词
for (List<String> groupWords:wordsByLength.values()){
int forTimes = 0;
System.out.println(groupWords);
List<String> words = groupWords;
for (int i=0;i<words.size();i++){
for (int j =i+1;j<words.size();j++){
if (isOneCharDiff(words.get(i), words.get(j))){
update(adjMap, words.get(i), words.get(j));
update(adjMap,words.get(j),words.get(i));
forTimes++;
}
}
}
System.out.println("forTime: "+forTimes);
}
return adjMap;
}
private static <KeyType> void update( Map<KeyType,List<String>> m, KeyType key, String value )
{
List<String> lst = m.get( key );
if( lst == null )
{
lst = new ArrayList<>( );
m.put( key, lst );
}
lst.add( value );
}
public static void main(String[] args) {
System.out.println(getAdjWords(wordList));
}
}
方案三:按照多个字母分组
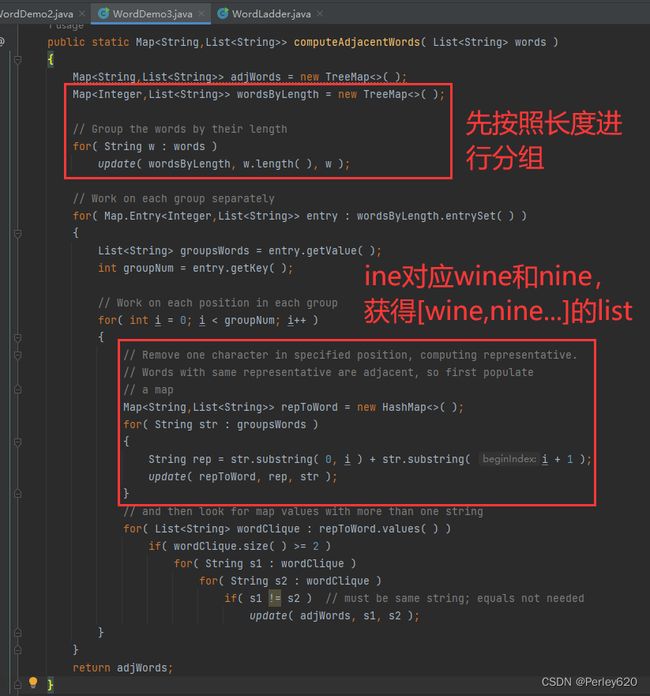
第3个算法更复杂,使用一些附加的映射!和前面一样,将单词按照长度分组,然后分别对每组运算。
为理解这个算法是如何工作的,假设我们对长度为4的单词操作。这时,首先要找出像wine和nine这样的单词对,它们除第1个字母外完全相同。
对于长度为4的每一个单词,一种做法是删除第1个字母,留下一个3字母单词代表。这样就形成一个M即,其中的关键字为这种代表,而其值是所有包含同一代表的单词的一个List。例如,在考虑4字母单词组的第1个字母时,代表“ine”对应“dine”“fine”“wine”“nine”“mine”“vine”“pine”“line”。代表“oot”对应“boot”“foot”“hoot”“loot”“soot”“zoot”。
每一个作为最后的Map的一个值的List对象都形成单词的一个集团,其中任何一个单词均可以通过单字母替换变成另一个单词,因此在这个最后的Map构成之后,很容易遍历它以及添加一些项到正在计算的原始Map中。然后,我们使用一个新的Map再处理4字母单词组的第2个字母。此后是第3个字母,最后处理第4个字母。
代码初步理解
package com.tianju.book.jpa.mapLearn;
import java.util.*;
public class WordDemo3 {
private static List<String> wordList = Arrays.asList(
"wine", "dine", "fine", "line", "mine", "nine", "pine", "vine", "wide",
"wife", "wipe", "wire", "wind", "wing", "wink", "wins");
// Computes a map in which the keys are words and values are Lists of words
// that differ in only one character from the corresponding key.
// Uses an efficient algorithm that is O(N log N) with a TreeMap, or
// O(N) if a HashMap is used.
public static Map<String,List<String>> computeAdjacentWords( List<String> words )
{
Map<String,List<String>> adjWords = new TreeMap<>( );
Map<Integer,List<String>> wordsByLength = new TreeMap<>( );
// Group the words by their length
for( String w : words )
update( wordsByLength, w.length( ), w );
// Work on each group separately
for( Map.Entry<Integer,List<String>> entry : wordsByLength.entrySet( ) )
{
List<String> groupsWords = entry.getValue( );
int groupNum = entry.getKey( );
// Work on each position in each group
for( int i = 0; i < groupNum; i++ )
{
// Remove one character in specified position, computing representative.
// Words with same representative are adjacent, so first populate
// a map
Map<String,List<String>> repToWord = new HashMap<>( );
for( String str : groupsWords )
{
String rep = str.substring( 0, i ) + str.substring( i + 1 );
update( repToWord, rep, str );
}
// and then look for map values with more than one string
for( List<String> wordClique : repToWord.values( ) )
if( wordClique.size( ) >= 2 )
for( String s1 : wordClique )
for( String s2 : wordClique )
if( s1 != s2 ) // must be same string; equals not needed
update( adjWords, s1, s2 );
}
}
return adjWords;
}
private static <KeyType> void update( Map<KeyType,List<String>> m, KeyType key, String value )
{
List<String> lst = m.get( key );
if( lst == null )
{
lst = new ArrayList<>( );
m.put( key, lst );
}
lst.add( value );
}
public static void main(String[] args) {
Map<String, List<String>> map = computeAdjacentWords(wordList);
System.out.println(map);
}
}
该算法的一种实现,其运行时间改进到4秒。虽然这些附加的Map使得算法更快,而且句子结构也相对清晰,但是程序没有利用到该Map的关键字保持有序排列的事实,
同样,有可能一种支持Map的操作但不保证有序排列的数据结构可能运行得更快,因为它要做的工作更少。第5章将探索这种可能性,并讨论隐藏在另一种Map实现背后的想法,这种实现叫作HashMap。HashMap将实现的运行时间从1秒减少到0.8秒。
原书代码
package com.tianju.book.jpa.mapLearn;
import java.io.*;
import java.util.List;
import java.util.Map;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.TreeMap;
import java.util.HashMap;
import java.util.Queue;
/*
DISTRIBUTION OF DICTIONARY:
Read the words...88984
1 1
2 48
3 601
4 2409
5 4882
6 8205
7 11989
8 13672
9 13014
10 11297
11 8617
12 6003
13 3814
14 2173
15 1169
16 600
17 302
18 107
19 53
20 28
Elapsed time FAST: 2.8 vs 3.8
Elapsed time MEDIUM: 50.9 vs 50.5
Elapsed time SLOW: 95.9 vs 96.1 (H vs T)
**/
public class WordLadder
{
public static List<String> readWords( BufferedReader in ) throws IOException
{
String oneLine;
List<String> lst = new ArrayList<>( );
while( ( oneLine = in.readLine( ) ) != null )
lst.add( oneLine );
return lst;
}
// Returns true is word1 and word2 are the same length
// and differ in only one character.
private static boolean oneCharOff( String word1, String word2 )
{
if( word1.length( ) != word2.length( ) )
return false;
int diffs = 0;
for( int i = 0; i < word1.length( ); i++ )
if( word1.charAt( i ) != word2.charAt( i ) )
if( ++diffs > 1 )
return false;
return diffs == 1;
}
private static <KeyType> void update( Map<KeyType,List<String>> m, KeyType key, String value )
{
List<String> lst = m.get( key );
if( lst == null )
{
lst = new ArrayList<>( );
m.put( key, lst );
}
lst.add( value );
}
// Computes a map in which the keys are words and values are Lists of words
// that differ in only one character from the corresponding key.
// Uses a quadratic algorithm (with appropriate Map).
public static Map<String,List<String>> computeAdjacentWordsSlow( List<String> theWords )
{
Map<String,List<String>> adjWords = new HashMap<>( );
String [ ] words = new String[ theWords.size( ) ];
theWords.toArray( words );
for( int i = 0; i < words.length; i++ )
for( int j = i + 1; j < words.length; j++ )
if( oneCharOff( words[ i ], words[ j ] ) )
{
update( adjWords, words[ i ], words[ j ] );
update( adjWords, words[ j ], words[ i ] );
}
return adjWords;
}
// Computes a map in which the keys are words and values are Lists of words
// that differ in only one character from the corresponding key.
// Uses a quadratic algorithm (with appropriate Map), but speeds things up a little by
// maintaining an additional map that groups words by their length.
public static Map<String,List<String>> computeAdjacentWordsMedium( List<String> theWords )
{
Map<String,List<String>> adjWords = new HashMap<>( );
Map<Integer,List<String>> wordsByLength = new HashMap<>( );
// Group the words by their length
for( String w : theWords )
update( wordsByLength, w.length( ), w );
// Work on each group separately
for( List<String> groupsWords : wordsByLength.values( ) )
{
String [ ] words = new String[ groupsWords.size( ) ];
groupsWords.toArray( words );
for( int i = 0; i < words.length; i++ )
for( int j = i + 1; j < words.length; j++ )
if( oneCharOff( words[ i ], words[ j ] ) )
{
update( adjWords, words[ i ], words[ j ] );
update( adjWords, words[ j ], words[ i ] );
}
}
return adjWords;
}
// Computes a map in which the keys are words and values are Lists of words
// that differ in only one character from the corresponding key.
// Uses an efficient algorithm that is O(N log N) with a TreeMap, or
// O(N) if a HashMap is used.
public static Map<String,List<String>> computeAdjacentWords( List<String> words )
{
Map<String,List<String>> adjWords = new TreeMap<>( );
Map<Integer,List<String>> wordsByLength = new TreeMap<>( );
// Group the words by their length
for( String w : words )
update( wordsByLength, w.length( ), w );
// Work on each group separately
for( Map.Entry<Integer,List<String>> entry : wordsByLength.entrySet( ) )
{
List<String> groupsWords = entry.getValue( );
int groupNum = entry.getKey( );
// Work on each position in each group
for( int i = 0; i < groupNum; i++ )
{
// Remove one character in specified position, computing representative.
// Words with same representative are adjacent, so first populate
// a map
Map<String,List<String>> repToWord = new HashMap<>( );
for( String str : groupsWords )
{
String rep = str.substring( 0, i ) + str.substring( i + 1 );
update( repToWord, rep, str );
}
// and then look for map values with more than one string
for( List<String> wordClique : repToWord.values( ) )
if( wordClique.size( ) >= 2 )
for( String s1 : wordClique )
for( String s2 : wordClique )
if( s1 != s2 ) // must be same string; equals not needed
update( adjWords, s1, s2 );
}
}
return adjWords;
}
// Find most changeable word: the word that differs in only one
// character with the most words. Return a list of these words, in case of a tie.
public static List<String> findMostChangeable( Map<String,List<String>> adjacentWords )
{
List<String> mostChangeableWords = new ArrayList<>( );
int maxNumberOfAdjacentWords = 0;
for( Map.Entry<String,List<String>> entry : adjacentWords.entrySet( ) )
{
List<String> changes = entry.getValue( );
if( changes.size( ) > maxNumberOfAdjacentWords )
{
maxNumberOfAdjacentWords = changes.size( );
mostChangeableWords.clear( );
}
if( changes.size( ) == maxNumberOfAdjacentWords )
mostChangeableWords.add( entry.getKey( ) );
}
return mostChangeableWords;
}
public static void printMostChangeables( List<String> mostChangeable,
Map<String,List<String>> adjacentWords )
{
for( String word : mostChangeable )
{
System.out.print( word + ":" );
List<String> adjacents = adjacentWords.get( word );
for( String str : adjacents )
System.out.println( " " + str );
System.out.println( " (" + adjacents.size( ) + " words)" );
}
}
public static void printHighChangeables( Map<String,List<String>> adjacentWords,
int minWords )
{
for( Map.Entry<String,List<String>> entry : adjacentWords.entrySet( ) )
{
List<String> words = entry.getValue( );
if( words.size( ) >= minWords )
{
System.out.print( entry.getKey( ) + " )" + words.size( ) + "):" );
for( String w : words )
System.out.print( " " + w );
System.out.println( );
}
}
}
// After the shortest path calculation has run, computes the List that
// contains the sequence of word changes to get from first to second.
public static List<String> getChainFromPreviousMap( Map<String,String> prev,
String first, String second )
{
LinkedList<String> result = new LinkedList<>( );
if( prev.get( second ) != null )
for( String str = second; str != null; str = prev.get( str ) )
result.addFirst( str );
return result;
}
// Runs the shortest path calculation from the adjacency map, returning a List
// that contains the sequence of words changes to get from first to second.
public static List<String> findChain( Map<String,List<String>> adjacentWords, String first, String second )
{
Map<String,String> previousWord = new HashMap<>( );
Queue<String> q = new LinkedList<>( );
q.add( first );
while( !q.isEmpty( ) )
{
String current = q.element( ); q.remove( );
List<String> adj = adjacentWords.get( current );
if( adj != null )
for( String adjWord : adj )
if( previousWord.get( adjWord ) == null )
{
previousWord.put( adjWord, current );
q.add( adjWord );
}
}
previousWord.put( first, null );
return getChainFromPreviousMap( previousWord, first, second );
}
// Runs the shortest path calculation from the original list of words, returning
// a List that contains the sequence of word changes to get from first to
// second. Since this calls computeAdjacentWords, it is recommended that the
// user instead call computeAdjacentWords once and then call other findChar for
// each word pair.
public static List<String> findChain( List<String> words, String first, String second )
{
Map<String,List<String>> adjacentWords = computeAdjacentWords( words );
return findChain( adjacentWords, first, second );
}
public static void run(String[] args) throws IOException {
long start, end;
FileReader fin = new FileReader( "D:\\Myprogram\\springboot-workspace\\spring-book-store\\spring-book-store\\src\\main\\java\\com\\tianju\\book\\jpa\\mapLearn\\dict.txt" );
BufferedReader bin = new BufferedReader( fin );
List<String> words = readWords( bin );
System.out.println(words);
Map<String,List<String>> adjacentWords;
adjacentWords = computeAdjacentWordsSlow( words );
System.out.println(adjacentWords);
}
public static void main( String [ ] args ) throws IOException
{
long start, end;
FileReader fin = new FileReader( "D:\\Myprogram\\springboot-workspace\\spring-book-store\\spring-book-store\\src\\main\\java\\com\\tianju\\book\\jpa\\mapLearn\\dict.txt" );
// FileReader fin = new FileReader( "dict.txt" );
BufferedReader bin = new BufferedReader( fin );
List<String> words = readWords( bin );
System.out.println( "Read the words..." + words.size( ) );
Map<String,List<String>> adjacentWords;
start = System.currentTimeMillis( );
adjacentWords = computeAdjacentWords( words );
end = System.currentTimeMillis( );
System.out.println( "Elapsed time FAST: " + (end-start) );
start = System.currentTimeMillis( );
adjacentWords = computeAdjacentWordsMedium( words );
end = System.currentTimeMillis( );
System.out.println( "Elapsed time MEDIUM: " + (end-start) );
start = System.currentTimeMillis( );
adjacentWords = computeAdjacentWordsSlow( words );
end = System.currentTimeMillis( );
System.out.println( "Elapsed time SLOW: " + (end-start) );
// printHighChangeables( adjacentWords, 15 );
System.out.println( "Adjacents computed..." );
List<String> mostChangeable = findMostChangeable( adjacentWords );
System.out.println( "Most changeable computed..." );
printMostChangeables( mostChangeable, adjacentWords );
BufferedReader in = new BufferedReader( new InputStreamReader( System.in ) );
for( ; ; )
{
System.out.println( "Enter two words: " );
String w1 = in.readLine( );
String w2 = in.readLine( );
List<String> path = findChain( adjacentWords, w1, w2 );
System.out.print( path.size( ) + "..." );
for( String word : path )
System.out.print( " " + word );
System.out.println( );
}
}
}
总结
1.B树,阶M,数据树叶上,根的儿子数在2和M之间,除根外,非树叶节点儿子为M/2和M之间;
2.B树的插入引起分裂,B树的删除,引起合并和领养;
3.红黑树,根是黑的,红色节点的儿子必须是黑的,所有路径的黑色节点数相同;
4.红黑树的插入,颜色翻转,单旋转,插入节点定颜色;
5.java标准库的set和map,使用红黑树;