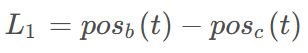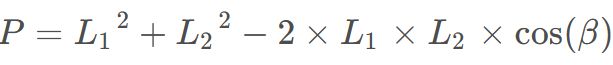改进蜣螂优化--采用莱维飞行和三角形游走策略
今天为大家带来一期改进的蜣螂优化算法。之前有篇文章推出过改进正弦算法引导的蜣螂优化算法(MSADBO),但是该文章已经有论文发表过了。
今天作者为大家带来的这一期改进,完全属于个人的改进,网络上应该查不到,大家也可以作为参考,也可以在作者改进的基础上接着改进。
改进策略如下:
①采用Cubic混沌映射,公式如下:
采用Cubic映射增加粒子多样性,可以减少粒子寻优时间,增加算法的收敛速度。想要采用别的混沌映射对算法改进的,可以参考这篇文章:10种混沌映射优化灰狼算法,可一键切换,可用于优化所有群智能算法,以灰狼算法为例进行介绍。
②采用三角形游走策略
在小蜣螂觅食阶段进行改进,在小蜣螂觅食阶段,不需要直接接近食物,可以在食物周围游走,增加蜣螂的随机性。三角形游走策略的公式如下:
再采用下述公式求出获得小蜣螂游走后得到的位置。
③Levy飞行与贪婪策略
Levy飞行是一种非常有效的提供随机因子的数学方法。Levy飞行可以提供步长符合Levy分布的随机游走方法。但Levy飞行有时步长过长,为了更加符合蜣螂觅食的行为,在Levy飞行乘以常数 C,从而减少步长。Levy飞行游走策略的公式如下所示。
levy飞行机制结束后,采用贪婪策略,如果粒子的适应度小于前一代适应度,则对粒子进行替换。
结果展示
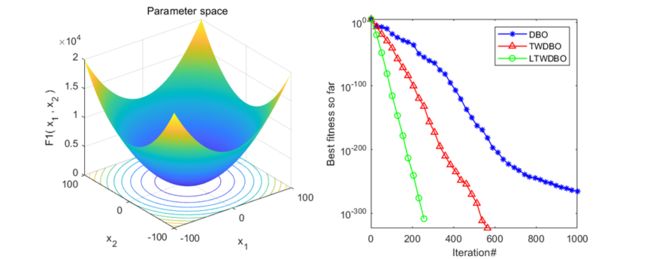
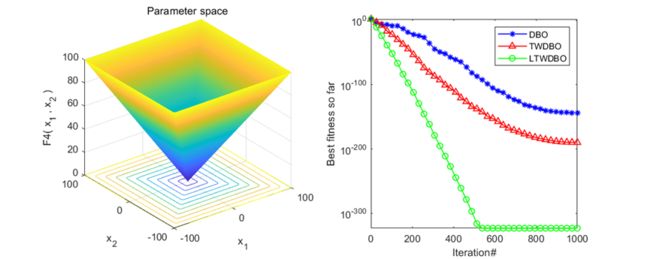
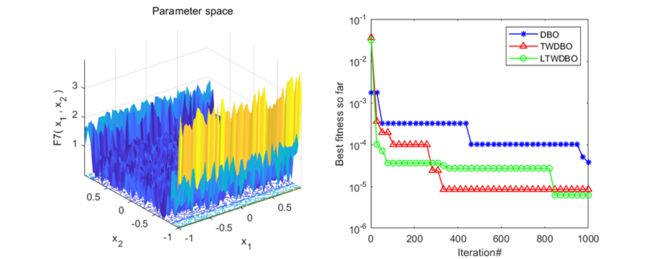
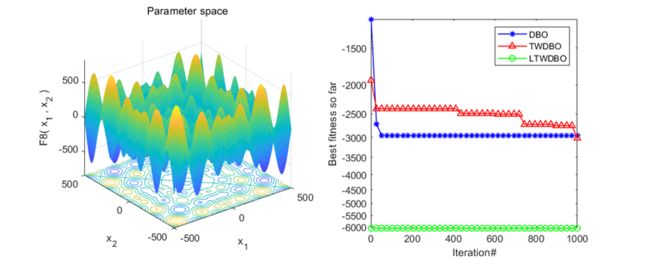
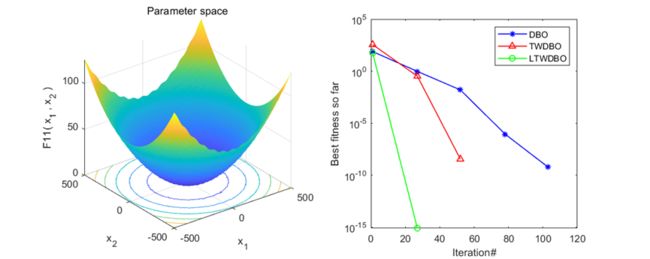
为了体现每个策略的必要性,作者对每个策略都进行了对比,其中DBO为原始的蜣螂算法,TWDBO为融合三角形游走策略的蜣螂算法,LTWDBO为融合莱维飞行和三角形游走策略的蜣螂算法。
这里截了一些图,可以看到效果还是非常不错的。
代码展示
clear all
clc
close
PD_no=50; %Number of sand cat
F_name='F11'; %Name of the test function
Max_iter=1000; %Maximum number of iterations
[LB,UB,Dim,F_obj]=CEC2005(F_name); %Get details of the benchmark functions
%% DBO
[Best_pos,Best_score, DBO_cg_curve ] = DBO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call DBO
fprintf ('Best solution obtained by DBO: %s\n', num2str(Best_score,'%e '));
display(['The best optimal value of the objective funciton found by DBO for ' [num2str(F_name)],' is : ', num2str(Best_pos)]);
%% TWDBO
[IBest_pos,IBest_score, TWDBO_cg_curve ] = TWDBO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call DBO
fprintf ('Best solution obtained by TWDBO: %s\n', num2str(IBest_score,'%e '));
display(['The best optimal value of the objective funciton found by TWDBO for ' [num2str(F_name)],' is : ', num2str(IBest_pos)]);
%% LTWDBO
[LTWDBOBest_pos,LTWDBOBest_score, LTWDBO_cg_curve ] = LTWDBO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call LTWDBO
fprintf ('Best solution obtained by LTWDBO: %s\n', num2str(LTWDBOBest_score,'%e '));
display(['The best optimal value of the objective funciton found by LTWDBO for ' [num2str(F_name)],' is : ', num2str(LTWDBOBest_pos)]);
%%
CNT=40;
k=round(linspace(1,Max_iter,CNT)); %随机选CNT个点
% 注意:如果收敛曲线画出来的点很少,随机点很稀疏,说明点取少了,这时应增加取点的数量,100、200、300等,逐渐增加
% 相反,如果收敛曲线上的随机点非常密集,说明点取多了,此时要减少取点数量
iter=1:1:Max_iter;
figure('Position',[154 145 894 357]);
subplot(1,2,1);
func_plot(F_name); % Function plot
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([F_name,'( x_1 , x_2 )'])
subplot(1,2,2); % Convergence plot
semilogy(iter(k),DBO_cg_curve(k),'b-*','linewidth',1);
hold on
semilogy(iter(k),TWDBO_cg_curve(k),'r-^','linewidth',1);
hold on
semilogy(iter(k),LTWDBO_cg_curve(k),'g-o','linewidth',1);
xlabel('Iteration#');
ylabel('Best fitness so far');
legend('DBO','TWDBO','LTWDBO');完整代码获取方式:后台回复关键字,不区分大小写。关键字:
LTWDBO