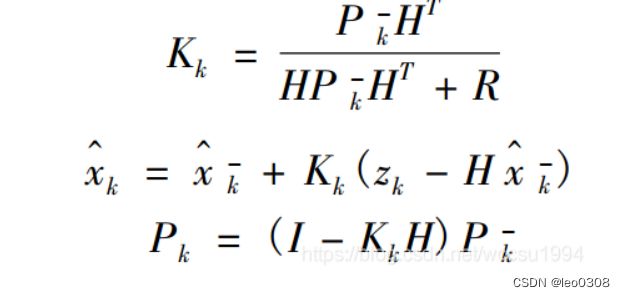python实现卡尔曼滤波代码详解
Kalman滤波算法的原理可以参考: 卡尔曼滤波理解
python中filterpy库中实现了各种滤波算法, 其中就包括了kalman滤波算法。
具体实现代码: https://github.com/rlabbe/filterpy/blob/master/filterpy/kalman/kalman_filter.py
本文针对该代码进行详细解读分析。
1 初始化及参数设置
需要设定的几个参数可参考: 详解多目标跟踪(MOT)算法中的Kalman滤波
- 状态变量的维度: dim_x
- 观测变量的维度:dim_z
- 状态变量:x, 初始化为大小为dim_x, 全0的列向量
- 观测变量:z, 初始化为大小为dim_z, 全0的列向量
- 状态转移矩阵: F, 初始化为维度为dim_x, 值为1的对角阵
- 状态变量协方差矩阵: P, 初始化为维度为dim_x, 值为1的对角阵
- 处理噪声写房产矩阵: Q, 初始化为维度为dim_x, 值为1的对角阵
- 测量矩阵:H,初始化为维度为(dim_z, dim_x)的全0矩阵
- 测量误差协方差矩阵: R, 初始化为维度为dim_z, 值为1的对角阵
def __init__(self, dim_x, dim_z, dim_u=0):
if dim_x < 1:
raise ValueError('dim_x must be 1 or greater')
if dim_z < 1:
raise ValueError('dim_z must be 1 or greater')
if dim_u < 0:
raise ValueError('dim_u must be 0 or greater')
self.dim_x = dim_x
self.dim_z = dim_z
self.dim_u = dim_u
self.x = zeros((dim_x, 1)) # state
self.P = eye(dim_x) # uncertainty covariance
self.Q = eye(dim_x) # process uncertainty
self.B = None # control transition matrix
self.F = eye(dim_x) # state transition matrix
self.H = zeros((dim_z, dim_x)) # measurement function
self.R = eye(dim_z) # measurement uncertainty
self._alpha_sq = 1. # fading memory control
self.M = np.zeros((dim_x, dim_z)) # process-measurement cross correlation
self.z = np.array([[None]*self.dim_z]).T
2 predict
def predict(self, u=None, B=None, F=None, Q=None):
"""
Predict next state (prior) using the Kalman filter state propagation
equations.
Parameters
----------
u : np.array, default 0
Optional control vector.
B : np.array(dim_x, dim_u), or None
Optional control transition matrix; a value of None
will cause the filter to use `self.B`.
F : np.array(dim_x, dim_x), or None
Optional state transition matrix; a value of None
will cause the filter to use `self.F`.
Q : np.array(dim_x, dim_x), scalar, or None
Optional process noise matrix; a value of None will cause the
filter to use `self.Q`.
"""
if B is None:
B = self.B
if F is None:
F = self.F
if Q is None:
Q = self.Q
elif isscalar(Q):
Q = eye(self.dim_x) * Q
# x = Fx + Bu
if B is not None and u is not None:
self.x = dot(F, self.x) + dot(B, u)
else:
self.x = dot(F, self.x)
# P = FPF' + Q
self.P = self._alpha_sq * dot(dot(F, self.P), F.T) + Q
# save prior
self.x_prior = self.x.copy()
self.P_prior = self.P.copy()
predict的过程比较简单, 就是根据上一次的状态变量, 估计当前的状态变量值, 同时更新状态变量的协方差。
3 update
def update(self, z, R=None, H=None):
"""
Add a new measurement (z) to the Kalman filter.
If z is None, nothing is computed. However, x_post and P_post are
updated with the prior (x_prior, P_prior), and self.z is set to None.
Parameters
----------
z : (dim_z, 1): array_like
measurement for this update. z can be a scalar if dim_z is 1,
otherwise it must be convertible to a column vector.
If you pass in a value of H, z must be a column vector the
of the correct size.
R : np.array, scalar, or None
Optionally provide R to override the measurement noise for this
one call, otherwise self.R will be used.
H : np.array, or None
Optionally provide H to override the measurement function for this
one call, otherwise self.H will be used.
"""
# set to None to force recompute
self._log_likelihood = None
self._likelihood = None
self._mahalanobis = None
if z is None:
self.z = np.array([[None]*self.dim_z]).T
self.x_post = self.x.copy()
self.P_post = self.P.copy()
self.y = zeros((self.dim_z, 1))
return
if R is None:
R = self.R
elif isscalar(R):
R = eye(self.dim_z) * R
if H is None:
z = reshape_z(z, self.dim_z, self.x.ndim)
H = self.H
# y = z - Hx
# error (residual) between measurement and prediction
self.y = z - dot(H, self.x)
# common subexpression for speed
PHT = dot(self.P, H.T)
# S = HPH' + R
# project system uncertainty into measurement space
self.S = dot(H, PHT) + R
self.SI = self.inv(self.S)
# K = PH'inv(S)
# map system uncertainty into kalman gain
self.K = dot(PHT, self.SI)
# x = x + Ky
# predict new x with residual scaled by the kalman gain
self.x = self.x + dot(self.K, self.y)
# P = (I-KH)P(I-KH)' + KRK'
# This is more numerically stable
# and works for non-optimal K vs the equation
# P = (I-KH)P usually seen in the literature.
I_KH = self._I - dot(self.K, H)
self.P = dot(dot(I_KH, self.P), I_KH.T) + dot(dot(self.K, R), self.K.T)
# save measurement and posterior state
self.z = deepcopy(z)
self.x_post = self.x.copy()
self.P_post = self.P.copy()
update的过程需要提供观测变量z。
1 首先计算卡尔曼增益。
2 计算当前观测值与通过观测矩阵得到的值之间的误差, 这个误差值乘上卡尔曼增益, 再加上predict过程得到的先验状态估计结果, 得到当前的卡尔曼滤波估计结果。
3 更新状态变量协方差矩阵。