读书笔记《数学建模算法与应用》第1-3章
目录
- 1. 线性规划
-
- 1.1 常规线性规划问题
- 1.2 转化为线性规划问题
- 1.3 投资的收益和风险
- 2. 整数规划
-
- 2.1 概论
- 2.2 0-1整数规划
-
- 2.2.1 相互排斥的约束条件
- 2.2.2 固定费用问题
- 2.2.3 指派问题
- 2.3 蒙特卡洛法(随机取样法)
- 2.4 整数线性规划的计算机求解
- 3. 非线性规划
-
- 3.1 非线性规划模型
- 3.2 无约束问题的matlab解法
-
- 3.2.1 无约束极值问题的符号解(精确解)
- 3.2.2 无约束极值问题的数值解
- 3.2.3 求函数零点和方程组的解
- 3.3 约束极值问题
-
- 3.3.1 二次规划
- 3.3.2 罚函数法
1. 线性规划
1.1 常规线性规划问题
解决问题: 例如如何利用现有资源来安排生产,以取得最大经济效益问题。
问题特征: 在一组线性约束条件的限制下,求一线性目标函数最大或最小的问题。
Matlab 求解:
% f 价值向量,注意分号隔开
f = [-2; -3; 5];
% a, b 线性不等式约束
a = [-2, 5, -1; 1, 3, 1]; b=[-10; 12];
% aeq, beq 线性等式约束
aeq = [1, 1, 1];
beq = 7;
% x 返回决策向量的取值,fval 返回目标函数最优值
[x,y] = linprog(f, a, b, aeq, beq, zeros(3,1));
x, y=-y
1.2 转化为线性规划问题
% 价值向量c=[1,2,3,4,1,2,3,4]^T 要注意这里是两组1:4
clc,clear
c=1:4;
c=[c,c]';
% 不等式约束的系数 注意上图标准型为A(u-v),进一步转化矩阵形式为[A,-A][u,v]^T≤b,所以这里的系数为[A,-A]这样的拼接矩阵
a=[1 -1 -1 1; 1 -1 1 -3; 1 -1 -2 3];
a=[a, -a];
b=[-2 -1 -1/2]';
[y,z]=linprog(c,a,b,[],[],zeros(8,1))
% 求解 x=u-v
x=y(1:4)-y(5:end)
1.3 投资的收益和风险
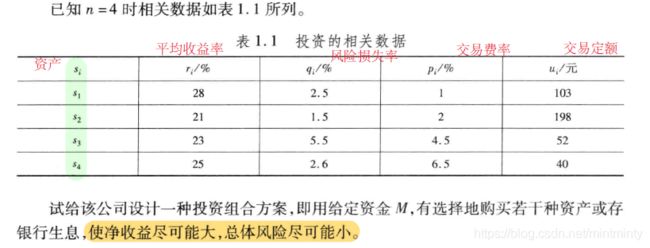
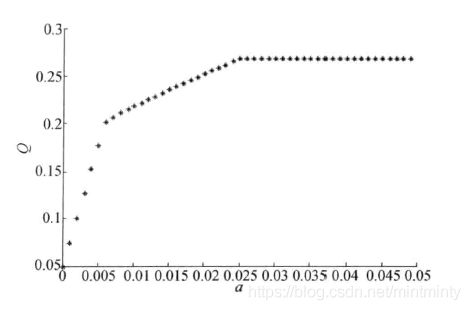
直观的建模, 目标函数满足收益尽可能大,总风险尽可能小:
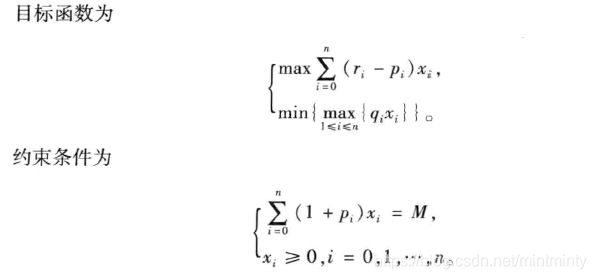
模型简化:
- 给风险一个界限 a a a,固定风险水平 优化收益

- 固定盈利水平,极小化风险
- 在权衡风险和收益两方面时,选择一个令自己满意的投资组合。因此对风险和收益分别赋予权重 s , 1 − s s, 1-s s,1−s

MATLAB矩阵合并
clc,clear
a=0;
hold on
while a<0.05
c=[-0.05,-0.27,-0.19,-0.185,-0.185];
% 投资方案为0-4,其中0表示存入银行 即无风险
% 逗号为横向拼接矩阵,拼接之后A维度为(4,5)
A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])];
b=a*ones(4,1);
Aeq=[1,1.01,1.02,1.045,1.065];
beq=1;
% LB决策变量下界
LB=zeros(5,1);
[x,Q]=linprog(c,A,b,Aeq,beq,LB);
Q=-Q;
plot(a,Q,'*k');
% 以0.001为步长 循环搜索
a=a+0.001;
end
xlabel('a'),ylabel('Q')
2. 整数规划
2.1 概论
- 变量全限制为整数时,为完全整数规划
- 变量部分限制为整数时,为混合整数规划
求解方法分类
- 分支定界法:求纯/混合整数线性规划
- 割平面法:求纯/混合整数线性规划
- 隐枚举法:求解0-1整数规划
- 匈牙利法:求解指派问题(0-1规划特殊情形)
- 蒙特卡洛法:求解各类规划
2.2 0-1整数规划
2.2.1 相互排斥的约束条件
这类问题的解决方法通常有两种,为保证 m m m 个约束条件中只有一个起作用,引入
2.2.2 固定费用问题
问题描述:目标是使成本最小,但某些固定费用的问题不能用一般线性规划描述,可改变为混合整数规划解决。


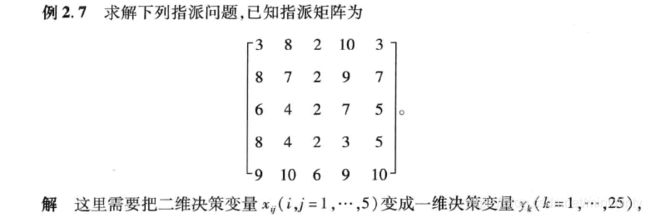
2.2.3 指派问题
略
2.3 蒙特卡洛法(随机取样法)
问题描述:基于对大量事件的统计结果来实现一些确定性问题的计算。
![]()
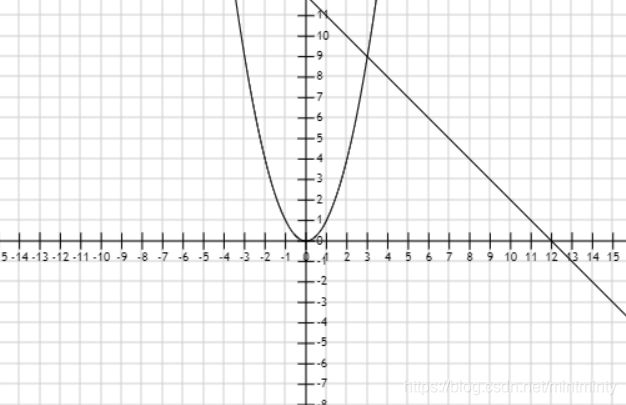
随机试验思想:
- 在矩形区域[0,12]x[0,9]上产生服从均匀分布的 1 0 7 10^7 107 个随机点
- 统计随机点落在曲边三角形的频数
- 曲边三角形的面积近似为矩形面积x频率
clc, clear
% unifrnd可以创建随机的连续均匀分布的数组
x=unifrnd(0,12,[1,10000000]);
y=unifrnd(0,9,[1,10000000]);
pinshu=sum(y<x.^2 & x<=3)+sum(y<12-x & x>=3);
area_appr=12*9*pinshu/10^7
除此之外,也可以利用蒙特卡洛解决非线性整数规划问题。
2.4 整数线性规划的计算机求解
Matlab中 intlinprog函数用法简介
matlab中的A( : )
对于整数线性规划问题,可以使用 matlab 的 intlinprog 函数求解,但必须将所有的决策变量转化为一维决策变量,变量替换后,约束条件很难写出。
Matlab 求解混合整数线性规划
x=intlinprog(f,intcon,A,b,Aeq,beq,lb,ub) ,其中intcon参数表示整数决策变量所在的位置,例如 x 1 , x 3 x_1, x_3 x1,x3是整数变量,则intcon=[1,3]
标准型: min x f ⊤ x \min _{x} f^{\top} x xminf⊤x
s.t. { x ( intcon ) 为整数, A ⋅ x ⩽ b Aeq ⋅ x = b e q 1 b ⩽ x ⩽ u b 0 \text { s.t. }\left\{\begin{array}{l} x(\text { intcon }) \text { 为整数, } \\ A \cdot x \leqslant b \\ \operatorname{Aeq} \cdot x=b e q \\ 1 b \leqslant x \leqslant u b_{0} \end{array}\right. s.t. ⎩⎪⎪⎨⎪⎪⎧x( intcon ) 为整数, A⋅x⩽bAeq⋅x=beq1b⩽x⩽ub0
clc,clear
% 目标函数系数
c=[3 8 2 10 3;8 7 2 9 7;6 4 2 7 5;8 4 2 3 5;9 10 6 9 10]
% (:)将矩阵c中的每列合并成一个长的列向量,结果大概为(3 8 2 10 3 8 7 2 9 7...9 10 6 9 10)^T
c=c(:);
% 2n个等式约束,n*n个变量
a=zeros(10,25);
# 整数决策变量的位置
intcon=1:25;
for i=1:5
% 前5个约束
a(i,(i-1)*5+1;5*i)=1;
% 后5个约束,i:5:25表示从i:25 每个数间隔5
a(5+i,i:5:25)=1;
end
b=ones(10,1);
lb=zeros(25,1);
ub=ones(25,1);
x=intlinprog(c,intcon,[],[],a,b,lb,ub);
x=reshape(x,[5,5])
clc,clear
f=[-3;-2;-1];
% 整数变量的位置
intcon=3;
% 第一个不等式约束
a=ones(1,3);b=7;
aeq=[4 2 1];beq=12;
lb=zeros(3,1);
% 上界,inf表示无穷大
un=[inf;inf;1];
x=intlinprog(f,intcon,a,b,aeq,beq,lb,ub)
3. 非线性规划
3.1 非线性规划模型
如果线性规划的最优解存在,则其最优解只能在其可行域的边界上达到(特别是可行域的顶点),而非线性规划的最优解(如果最优解存在)则可能在其可行域的任意一点达到。

[x,fval]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
fun是用M文件定义的函数f(x)x0是x的初始值nonlcon是用M文件定义的非线性向量函数c(x),ceq(x)options定义优化参数
% 编写M函数fun1.m定义目标函数
function f = fun1(x);
f=sum(x.^2)+8; % x.代表每个元素都取平方
% 编写M函数fun2.m定义非线性约束条件
function[g,h] = fun2(x);
g=[-x(1)^2+x(2)-x(3)^2
x(1)+x(2)^2+x(3)^3-20]; % 非线性不等式约束
h=[-x(1)-x(2)^2+2
x(2)+2*x(3)^2-3]; % 非线性等式约束
% 主程序文件
[x,y]=fmincon('fun1',rand(3,1),[],[],[],[],zeros(3,1),[],'fun2')
3.2 无约束问题的matlab解法
3.2.1 无约束极值问题的符号解(精确解)
clc,clear
syms x y % syms定义为符号变量,才能使用solve()
f=x^3-y^3+3*x^2+3*y^2-9*x;
df=jacobian(f); % 一阶偏导数
d2f=jacobian(df); % 海塞矩阵
[xx,yy]=solve(df); % 求驻点,solve()用于求解
xx=double(xx);yy=double(yy); % 转化成双精度浮点型数据
% 判断特征值正负
for i=1:length(xx)
a=subs(d2f,{x,y},{xx(i),yy(i)}); % 替换函数,将d2f中的{x,y}替换为{xx(i),yy(i)}
b=eig(a); % 求矩阵特征值用以判断海塞矩阵的正定性
f=subs(f,{x,y},{xx(i),yy(i)});
f=double(f);
if all(b>0)
fprintf('(%f,%f)是极小值点,对应极小值为%f\n',xx(i),yy(i),f);
elseif any(b>0)&any(b<0)
fprintf('(%f,%f)不是极小值点',xx(i),yy(i));
else
fprintf('无法判断(%f,%f)是不是极值点\n',xx(i),yy(i));
end
end
3.2.2 无约束极值问题的数值解
[x,fval]=fminunc(fun,x0,options) 或 [x,fval]=fminsearch(fun,x0,options)
fun是一个M函数x0是x的初始值options是优化参数,可以使用默认参数
clc,clear
f=@(x) x(1)^3-x(2)^3+3*x(1)^2+3*x(2)^2-9*x(1); % 定义匿名函数
g=@(x) -f(x);
[xy1,z1]=fminunc(f,rand(2,1)); % 求极小值点
[xy2,z2]=fminsearch(g,rand(2,1)); % 求极大值点
xy2,z2=-z2;
![]()
function [f,g]=fun3(x);
f=100*(x(2)-x(1)^2)^2+(1-x(1))^2;
g=[-400*x(1)*(x(2)-x(1)^2)-2*(1-x(1));200*(x(2)-x(1)^2)]; %x1和x2的梯度
% 主程序文件
options=optimset('GradObj','on'); % ‘Gradobj’指用户自定义的目标函数梯度
[x,y]=fminunc('fun3',rand(1,2),options);
3.2.3 求函数零点和方程组的解
clc,clear
xishu=[1 -1 2 -3]; % 多项式用向量定义,系数从高次幂到低次幂排列
x0=roots(xishu); % 返回由p表示的多项式的根作为列向量
% 使用符号解求解
syms x
x0=solve(x^3-x^2+2*x-3);
x0=vpa(x0,5); % 化成小数格式的数据
% 求数值解
y=@(x) x^3-x^2+2*x-3;
x=fsolve(y,rand); % 只能求给定初始解附近的一个零点
3.3 约束极值问题
3.3.1 二次规划

[x,fval]=quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)
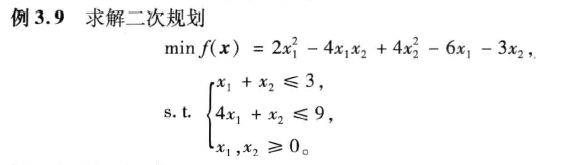
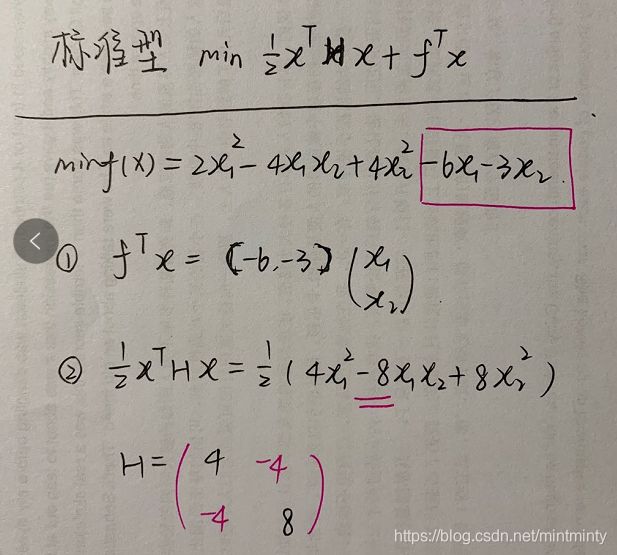
h=[4,-4;-4,8];
f=[-6;-3];
a=[1,1;4,1];
b=[3;9];
[x,value]=quadprog(h,f,a,b,[],[],zeros(2,1))
3.3.2 罚函数法
- 罚函数法可用于求解非线性规划问题,利用问题中的约束函数作出适当的罚函数,由此构造出带参数的增广目标函数,把问题转化为无约束非线性规划问题。
- 每次求解只能求出一个局部最优解,并且每次运行结果不同。如果非线性规划问题要求实施算法,则可用该方法,但计算精度较低。