算法-动态规划
这里写目录标题
-
- 1.最长回文子串
- 2.括号生成
- 3.跳跃游戏
- 4.跳跃游戏Ⅱ
- 最长回文串
- 找路子
- 爬楼梯方法
- 爬楼梯花费
- 打家劫舍
- 打家劫舍Ⅱ
- 删除并获得点数
- 单词拆分
- 哈密顿
- 跳跃游戏
- 跳跃游戏Ⅱ
- 最大子序和
- 环状最大子序和
- 乘积最大子数组
- 乘积为正的最长子数组长度
- 单词拆分
- 接雨水
- 矩阵区域和
- 二维区域和检索
- 下降路径最小和
- 三角形最小路径和
- 丑数
- 不同的二叉搜索树
- 等差数列划分
- 解码方法
1.最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
class Solution {
public:
string longestPalindrome(string s) {
int N=s.size();
int l=0,r=0;
vector<vector<int>> dp=vector<vector<int>>(N,vector<int>(N,0));
for(int i=N-1;~i;i--){
for(int j=i;j<N;j++){
if(i==j){
dp[i][j]=1;
}else if(j==i+1){
dp[i][j]=s[i]==s[j];
}else{
dp[i][j]=dp[i+1][j-1]&&s[i]==s[j];
}
if(dp[i][j]&&j-i+1>r-l+1){
l=i,r=j;
}
}
}
return s.substr(l,r-l+1);
}
};
心得总结
这题之前做过但还是做不出来过了几个月,自己真的垃圾
切入点:
因为是求最长,所以可以用动态规划来做。因为动态规划遍历过程中要记录下状态嘛,可以帮助我们来判断某子串是不是回文串。
问题来了,怎么记录回文子串呢?
子串得知道首尾,所以可以用二维的动态规划来做,当然一维也能做,一维比二维要抽象啊,先二维成功再想一维来优化对吧?
因为二维数组的下标就可以计算出回文子串的长度了对吧,也能确定是哪个回文子串,所以不用做过多的处理了。
当前状态可以由子状态加判断当前遍历的值来进行判断对吧,因为回文字符串是连续的啊又不能断。
2.括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
class Solution {
public:
vector<string> generateParenthesis(int n) {
vector<string> res;
generate(res,"",0,0,n);
return res;
}
void generate(vector<string> &res,string ans,int count1,int count2,int n){
if(count1>n||count2>n) return;
if(count1==n&&n==count2) res.push_back(ans);
if(count1>=count2){
generate(res,ans+"(",count1+1,count2,n);
generate(res,ans+")",count1,count2+1,n);
}
}
};
心得体会
切入点:
左括号和右括号同时贪,贪的同时判断一下右括号不能比左括号多,多了就废了就行了。
3.跳跃游戏
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
class Solution {
public:
typedef pair<int,int> PII;
bool canJump(vector<int>& nums) {
int N=nums.size();
queue<PII> q;
vector<int> st=vector<int>(N,0);
q.push({nums[0],0});
st[0]=1;
int f=nums[0];
if(f>=N-1) return true;
while(!q.empty()){
PII t=q.front();
q.pop();
for(int i=t.second;i<=t.second+t.first&&i<N;i++){
if(!st[i]){
q.push({nums[i],i});
f=max(f,t.second+t.first);
if(f>=N-1) return true;
st[i]=1;
}
}
}
return false;
}
};
class Solution {
public:
bool canJump(vector<int>& nums) {
int N=nums.size();
int farMost=0;//当前区间的右边界
if(nums.size()==0)
return true;
for(int i=0;i<N;i++){
if(i<=farMost){//从区间的点里找能到的最远的距离
farMost=max(farMost,i+nums[i]);//更新最远距离
if(farMost>=N-1)
return true;
}
}
return false;
}
};
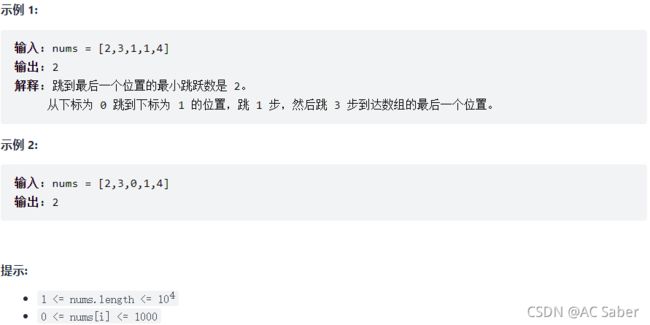
4.跳跃游戏Ⅱ
给你一个非负整数数组 nums ,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。
class Solution {
public:
int jump(vector<int>& nums) {
int N=nums.size();
int end=0;
int f=0;
int step=0;
for(int i=0;i<N-1;i++){
f=max(f,nums[i]+i);//找最远的
if(end==i){//如果end是小于N-2的,那i迟早会用完它里面的点
//所以end必定会更新超过N-2,一旦超过,
//i就无法超过end,也就不会再增加步数了,所以步数不会多的。
step++;
end=f;
}
}
return step;
}
};
目录
-
- 1.最长回文子串
- 2.括号生成
- 3.跳跃游戏
- 4.跳跃游戏Ⅱ
- 最长回文串
- 找路子
- 爬楼梯方法
- 爬楼梯花费
- 打家劫舍
- 打家劫舍Ⅱ
- 删除并获得点数
- 单词拆分
- 哈密顿
- 跳跃游戏
- 跳跃游戏Ⅱ
- 最大子序和
- 环状最大子序和
- 乘积最大子数组
- 乘积为正的最长子数组长度
- 单词拆分
- 接雨水
- 矩阵区域和
- 二维区域和检索
- 下降路径最小和
- 三角形最小路径和
- 丑数
- 不同的二叉搜索树
- 等差数列划分
- 解码方法
最长回文串
注:区别于公共子序列
class Solution {
public:
string longestPalindrome(string s) {
int b=0, l=0;//起点,终点指针
bool dp[1000][1000] = { false };
for (int i = s.length() - 1; i >= 0; i--) {//向前遍历起点指针,避免数据串联,
for (int j = i; j < s.length(); j++) {//遍历终点指针
if (j == i) dp[i][j] = true;
else if (j == i + 1) dp[i][j] =s[i] == s[j];
else {
dp[i][j] = dp[i + 1][j - 1] && s[i] == s[j];
}
if (dp[i][j]) {//看是不是最长的
if (l - b < j - i) {
b = i, l = j;
}
}
}
}
return s.substr(b, l - b + 1);
}
};
找路子
class Solution {
public:
int getMaxValue(vector<vector<int>>& grid) {
int n=grid.size(),m=grid[0].size();//为了方便
vector<vector<int>> dp(n+1,(vector<int>(m+1)));//vector的构造函数
for(int i=1;i<=n;i++){//从1开始是为了避免下标小于0的问题
for(int j=1;j<=m;j++){
dp[i][j]=max(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];
//grid数组下标还是从0开始的
}
}
return dp[n][m];
}
};
爬楼梯方法
class Solution {
public:
int climbStairs(int n) {
int dp[1010] = { 0 };
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
dp[i]=dp[i-1]+dp[i-2];//最后一步可以走一步或两步
}
return dp[n];
}
};
爬楼梯花费
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int top=cost.size();
int dp[1010]={0};
for(int i=2;i<=top;i++){
dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
//看走一步还是两步开销小
}
return dp[top];
}
};
打家劫舍
class Solution {
public:
int rob(vector<int>& nums) {
if(!nums.size())
return 0;
if(nums.size()==1)
return nums[0];
vector<int> dp=vector<int>(nums.size(),0);
dp[0]=nums[0];
dp[1]=max(nums[0],nums[1]);
for(int i=2;i<nums.size();i++){
dp[i]=max(dp[i-1],dp[i-2]+nums[i]);//打这家,前一家就不能打
}
return dp[nums.size()-1];
}
};
打家劫舍Ⅱ
class Solution {
public:
int rob(vector<int>& nums) {
int N=nums.size();
vector<int> dp=vector<int>(N,0);
vector<int> dp2=vector<int>(N,0);
if(nums.size()==1) return nums[0];
if(nums.size()==2) return max(nums[0],nums[1]);
dp[0]=nums[0];//1
dp[1]=max(nums[0],nums[1]);//3
for(int i=2;i<N-1;i++){
dp[i]=max(dp[i-1],dp[i-2]+nums[i]);
}
dp2[1]=nums[1];//3
for(int i=2;i<N;i++){
dp2[i]=max(dp2[i-1],dp2[i-2]+nums[i]);
}
return dp2[N-1]>dp[N-2]?dp2[N-1]:dp[N-2];
//就看看要第一家和要最后一家谁更赚
}
};
删除并获得点数
class Solution {
public:
int deleteAndEarn(vector<int>& nums) {
int N=nums.size();
vector<int> trans=vector<int>(10010,0);
for(int i=0;i<N;i++){
trans[nums[i]]+=nums[i];//发现规律后转成set就变成打家劫舍了
}
vector<int> dp=vector<int>(10010);
dp[0]=0;
dp[1]=trans[1];
for(int i=2;i<trans.size();i++){
dp[i]=max(dp[i-2]+trans[i],dp[i-1]);
}
cout<<dp.size()<<endl;
return dp[dp.size()-1];
}
};
单词拆分
哈密顿
#include跳跃游戏
其实也可看做走一步用一个能量,到了一个点上看捡地上的能量还是要自己手上的,二者取最大

class Solution {
public:
bool canJump(vector<int>& nums) {
int N=nums.size();
int farMost=0;//当前区间的右边界
if(nums.size()==0)
return true;
for(int i=0;i<N;i++){
if(i<=farMost){//从区间的点里找能到的最远的距离
farMost=max(farMost,i+nums[i]);//更新最远距离
if(farMost>=N-1)
return true;
}
}
return false;
}
};
跳跃游戏Ⅱ
class Solution {
public:
int jump(vector<int>& nums) {
int maxPos=0,n=nums.size(),end=0,step=0;
//从区间里的点能到的最远距离,区间的边界
for(int i=0;i<n-1;i++){
if(maxPos>=i){//在区间内
maxPos=max(maxPos,nums[i]+i);//寻找能到的最远边界
if(i==end){//当前状态的区间的点用完了,更新区间、步数
step++;
end=maxPos;
}
}
}
return step;
}
};
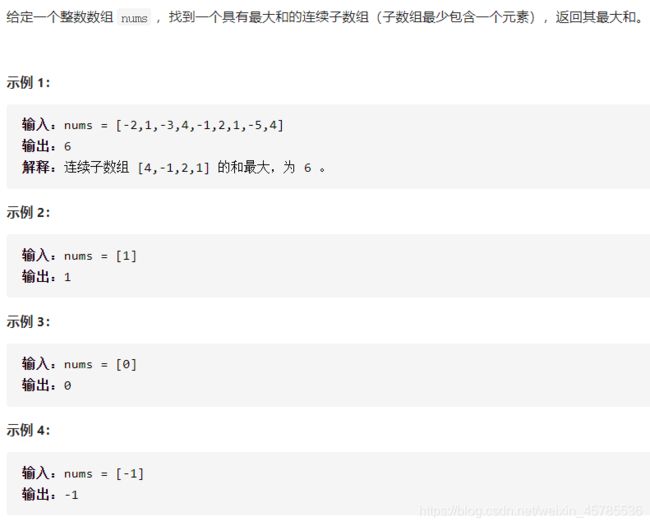
最大子序和
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int N=nums.size();
int res=INT_MIN;
if(N==1) return nums[0];
int dp=-1;
for(int i=0;i<N;i++){
dp=max(nums[i],dp+nums[i]);
//dp代表以i为截点
//最新的子序列的和,两个状态的计算:不要之前子序列(子序列和小于0了)
//和要之前子序列(还是大于0)
res=max(res,dp);
}
return res;
}
};
环状最大子序和
class Solution {
public:
int maxSubarraySumCircular(vector<int>& nums) {
int N=nums.size();
int dp1=-1;
int dp2=1;
int res1=INT_MIN,res2=INT_MAX;
//分三种情况,最大和的子序跨环/不跨环/序列全为负数
//跨环就是用总和减去不跨环的最小和,全负数是因为sum-res2>=0,不可能是跨环的。
//并且跨环可以看作是从两头出发找最大,意思是两头必包含
int sum=0;
for(int i=0;i<N;i++){
sum+=nums[i];
dp1=max(dp1+nums[i],nums[i]);
res1=max(res1,dp1);
dp2=min(dp2+nums[i],nums[i]);
res2=min(dp2,res2);
}
if(res1<0) return res1;
return res1>(sum-res2)?res1:(sum-res2);
}
};
乘积最大子数组
/**
* @param {number[]} nums
* @return {number}
*/
var maxProduct = function(nums) {
let N=nums.length
let res=nums[0]
let dp1=1//正子数组
let dp2=1//负子数组
for(let i=0;i<N;i++){
if(nums[i]<0){
[dp1,dp2]=[dp2,dp1]//交换
}
dp1=Math.max(dp1*nums[i],nums[i])//最大
dp2=Math.min(dp2*nums[i],nums[i])//最小,算最小是因为它有可能翻身变最大
res=Math.max(res,dp1)
}
return res
};
乘积为正的最长子数组长度
/**
* @param {number[]} nums
* @return {number}
*/
var getMaxLen = function(nums) {
let z=0,f=0;//正的,负的
let res=Number.MIN_VALUE
let N=nums.length;
for(let i=0;i<N;i++){
if(!nums[i]){//0就都断了
z=0
f=0
}else if(nums[i]<0){//正负交换,负增加,前面有正的话正也加,因为可能翻身变负
[z,f]=[f,z]
f++
if(z>0) z++
}else{//正增加,前面有负的话负也加,因为可能翻身变正
z++
if(f>0) f++
}
res=Math.max(z,res)//都是要正的最大
}
return res
};
单词拆分
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
int N=s.size();
vector<int> dp=vector<int>(N+1,0);//表示当前子串能不能拆
dp[0]=1;
for(int i=1;i<=N;i++){
for(int j=0;j<i;j++){
if(dp[j]&&find(wordDict.begin(),wordDict.end(),s.substr(j,i-j))!=wordDict.end()){
// 子串左边部分能并且右边也在字典里
dp[i]=1;//当前子串可拆
break;
}
}
}
return dp[N];
}
};
接雨水
class Solution {
public:
int trap(vector<int>& height) {
int N=height.size();
if(N==0) return 0;
vector<int> dp1=vector<int>(N,0);//左边最大高度
vector<int> dp2=vector<int>(N,0);//右
dp1[0]=height[0];
for(int i=1;i<N;i++){
dp1[i]=max(dp1[i-1],height[i]);
}
dp2[N-1]=height[N-1];
for(int i=N-2;i>=0;i--){
dp2[i]=max(dp2[i+1],height[i]);
}
int ans=0;
for(int i=0;i<N;i++){//左右阴影覆盖就是能装的,画图看看哈
ans+=min(dp1[i],dp2[i])-height[i];
}
return ans;
}
};
矩阵区域和
class Solution {
public:
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
int M=mat.size();
int N=mat[0].size();
vector<vector<int>> dp=vector<vector<int>>(M+1,vector<int>(N+1,0));
vector<vector<int>> res=vector<vector<int>>(M,vector<int>(N,0));
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
dp[i + 1][j + 1] = dp[i][j + 1] + dp[i + 1][j] - dp[i][j] + mat[i][j];
}
}
for(int i=0;i<M;i++){
for(int j=0;j<N;j++){
// 左上角坐标
int r1 = max(i - k, 0);
int c1 = max(j - k, 0);
// 右下角坐标
int r2 = min(i + k, M - 1);
int c2 = min(j + k, N - 1);
res[i][j] = dp[r2 + 1][c2 + 1] - dp[r1][c2 + 1] - dp[r2 + 1][c1] + dp[r1][c1];
}
}
return res;
}
};
二维区域和检索
class NumMatrix {
public:
vector<vector<int>> dp;
NumMatrix(vector<vector<int>>& matrix) {
int N=matrix.size();
int M=matrix[0].size();
dp=vector<vector<int>>(N+1,vector<int>(M+1,0));
for(int i=0;i<N;i++){
for(int j=0;j<M;j++){
dp[i+1][j+1]=dp[i+1][j]+dp[i][j+1]-dp[i][j]+matrix[i][j];
}
}
}
int sumRegion(int row1, int col1, int row2, int col2) {
int res=0;
res+=dp[row2+1][col2+1]-dp[row2+1][col1]-dp[row1][col2+1]+dp[row1][col1];
return res;
}
};
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix* obj = new NumMatrix(matrix);
* int param_1 = obj->sumRegion(row1,col1,row2,col2);
*/
下降路径最小和
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& matrix) {
int N=matrix.size();
vector<vector<int>> dp=vector<vector<int>>(N+1,vector<int>(N+2,101));
int res=INT_MAX;
for(int i=0;i<=N;i++) dp[0][i]=0;
for(int i=1;i<=N;i++){
for(int j=1;j<=N;j++){
dp[i][j]=matrix[i-1][j-1]+min(dp[i-1][j-1],min(dp[i-1][j],dp[i-1][j+1]));
}
}
for(int i=1;i<=N;i++) res=min(res,dp[N][i]);
return res;
}
};
三角形最小路径和
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
int N=triangle.size();
vector<vector<int>> dp=vector<vector<int>>(N+1,vector<int>(N+1,10001));
for(int i=0;i<=N;i++) dp[0][i]=0;
for(int i=1;i<=N;i++){
for(int j=1;j<=i;j++){
dp[i][j]=triangle[i-1][j-1]+min(dp[i-1][j],dp[i-1][j-1]);
}
}
int res=INT_MAX;
for(int i=1;i<=N;i++){
res=min(res,dp[N][i]);
}
return res;
}
};
丑数
class Solution {
public:
int nthUglyNumber(int n) {
vector<int> dp=vector<int>(n,1);
int d1=0,d2=0,d3=0;
int a,b,c;
int minDp;
for(int i=1;i<n;i++){
a=dp[d1]*2,b=dp[d2]*3,c=dp[d3]*5;
minDp=min(min(a,b),c);
if(minDp==a) d1++;
if(minDp==b) d2++;
if(minDp==c) d3++;
dp[i]=minDp;
}
// for(int i=0;i
return dp[n-1];
}
};
不同的二叉搜索树
class Solution {
public:
int numTrees(int n) {
// dp[n]=dp[i]*dp[n-i]
vector<int> dp=vector<int>(n+1,0);
dp[0]=dp[1]=1;
for(int i=2;i<=n;i++){
for(int j=1;j<=i;j++){
dp[i]+=dp[j-1]*dp[i-j];
}
}
return dp[n];
}
};
等差数列划分
class Solution {
public:
int numberOfArithmeticSlices(vector<int>& nums) {
int res=0;
int N=nums.size();
if(N==1) return 0;
if(N==2) return 0;
vector<int> dp=vector<int>(N,0);
for(int j=2;j<N;j++){
int d=nums[j-1]-nums[j-2];
if(d==(nums[j]-nums[j-1])){
dp[j]++;
dp[j]+=dp[j-1];
res+=dp[j];
}
}
return res;
}
};
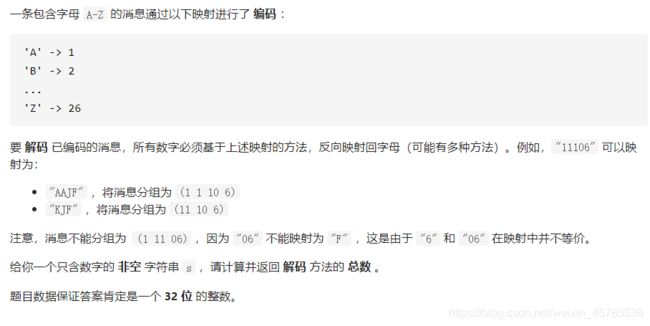
解码方法
class Solution {
public:
int numDecodings(string s) {
int N=s.size();
int res=0;
vector<int> dp=vector<int>(N,0);
if(s[0]=='0') return 0;
else{
dp[0]=1;
res+=1;
}
if(N==1) return res;
if((s[0]!='0'&&s[1]!='0')&&(((s[0]-'0')*10+s[1]-'0')>0&&((s[0]-'0')*10+s[1]-'0')<27)) {
dp[1]=2;
}else if(s[1]=='0'&&s[0]-'0'>2){
return 0;
}
else {
dp[1]=1;
}
for(int i=2;i<N;i++){
if(s[i]=='0'&&s[i-1]=='0'){
return 0;
}else if(s[i]=='0'&&((s[i-1]-'0')*10+s[i]-'0')>0&&((s[i-1]-'0')*10+s[i]-'0')<27){
dp[i]=dp[i-2];
}else if(s[i-1]!='0'&&((s[i-1]-'0')*10+s[i]-'0')>0&&((s[i-1]-'0')*10+s[i]-'0')<27){
dp[i]=dp[i-1]+dp[i-2];
}else if(s[i]=='0'){
return 0;
}else{
dp[i]=dp[i-1];
}
}
return dp[N-1];
}
};