二叉树---前，中，后序遍历做题技巧（前，中，后，层次，线索二叉树）

1.由二叉树求前，中，后序遍历

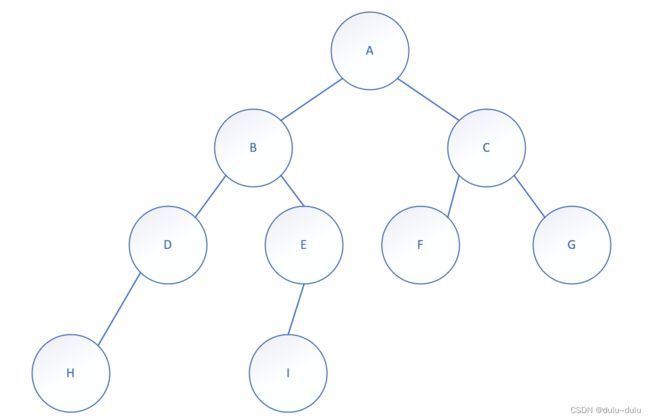
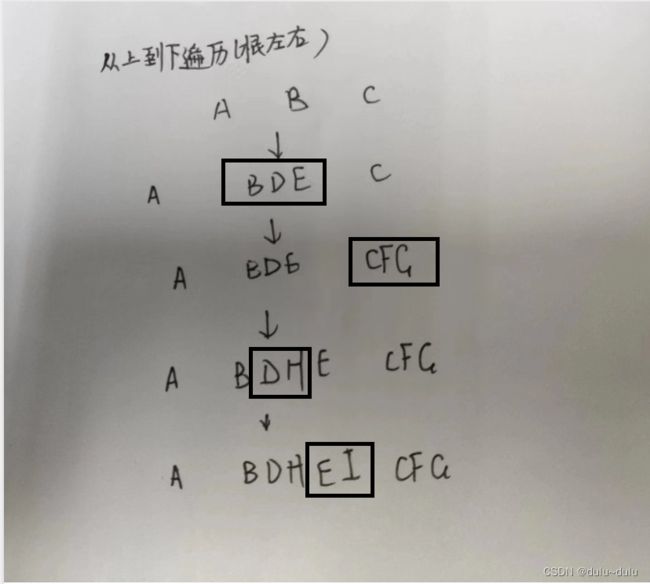
 前序:根左右（每一个小方块都遵循）

 得到：A,B,D,H,E,I,C,F,G

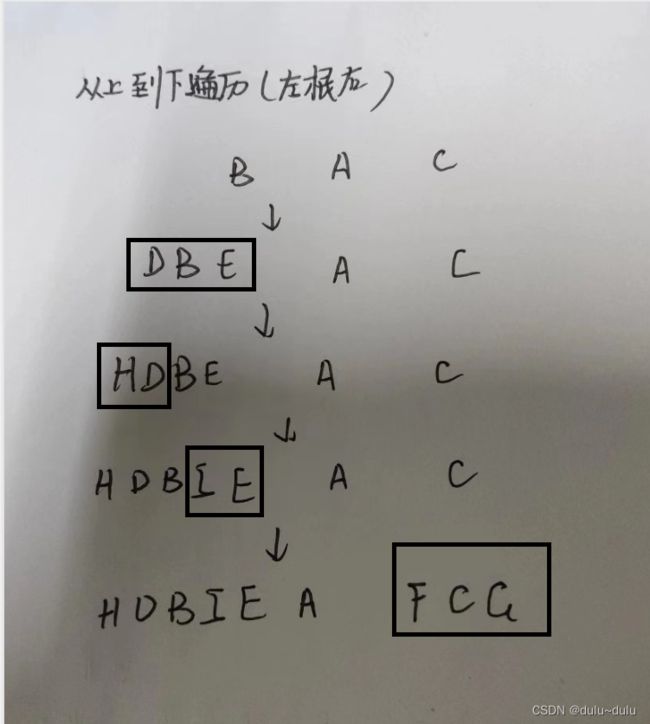
中序：左根右（每一个小方块都遵循）

 得到：H,D,B,I,E,A,F,C,G

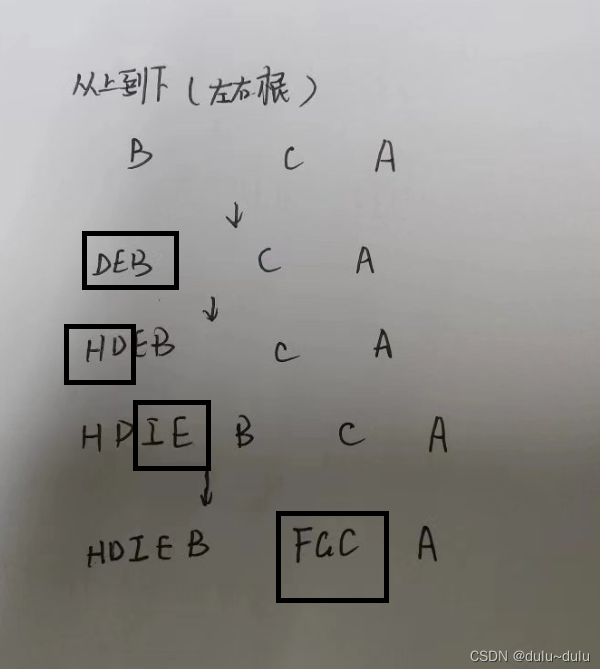
后序：左右根（每一个小方块都遵循）

 

 得到：H,D,I,E,B,F,G,C,A

 

2.由先序，中序或后序，中序得到其余序列

巧妙做法

参考b站“蛮蛮壮”记录的做题技巧

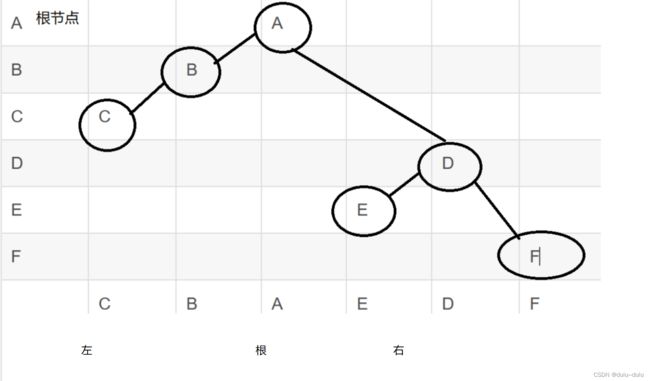
（1）.一棵二叉树的先序遍历序列为A,B,C,D,E,F,中序遍历序列为C,B,A,E,D,F,则后序遍历序列为

A			A
B		B
C	C
D					D
E				E
F						F
	C	B	A	E	D	F

再做如下转换

左子树所有节点在父节点的左边，右子树所有节点在父节点的右边

得到后序遍历为C,B,E,F,D,A

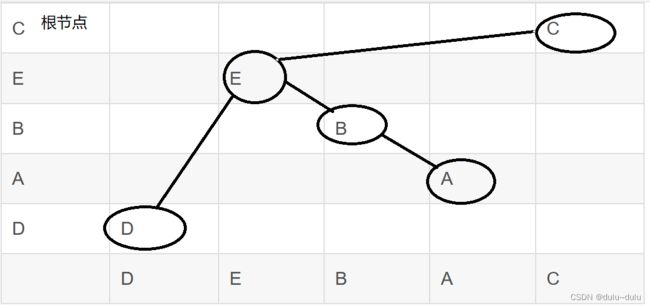
（2）.一棵二叉树的后序遍历为D,A,B,E,C,中序遍历为D,E,B,A,C,则先序遍历序列为

C					C
E		E
B			B
A				A
D	D
	D	E	B	A	C

转换一下 

得到先序遍历的结果为：C,E,D,B,A

 个人理解

•只有中序和先序或者中序和后序才能确定一个二叉树

•中序遍历是左根右，描述的是一棵树水平节点的顺序，作行，后序遍历和先序遍历可以确定根的位置，将根摆在最上端，而左右就从中序遍历判断

•多做几道题，可以领悟到以下技巧

•父节点在子节点的上方

•左子树所有节点在父节点的左边，右子树所有节点在父节点的右边

常规的做法

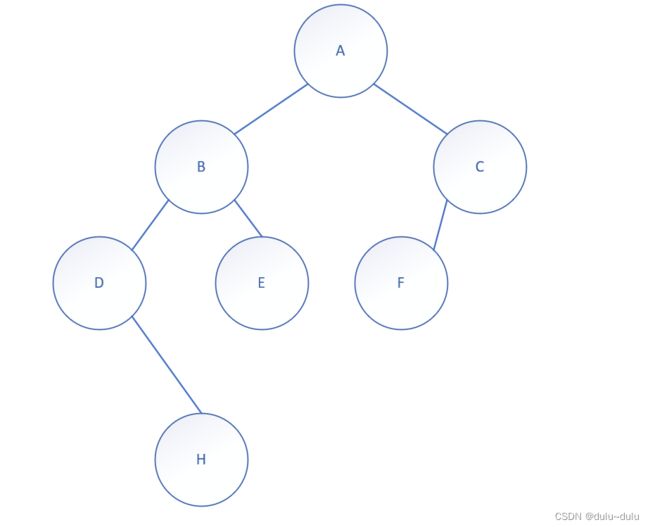
前序序列：A,B,D,H,E,C,F

中序遍历：D,H,B,E,A,F,C

•由前序序列知，A是根节点，那么D,H,B,E是左子树，F,C是右子树

•将D,H,B,E带到前序序列中为B,D,H,E，得到B是父节点，同样，将F,C带到前序中为C,F，得到C是父节点

•再将B带到中序遍历中，得到左右子树分别为D,H和E，而C的左子树是F

•D,H再带到前序遍历中，得到D,H，所以父节点是D，至此得到二叉树

总结：

•中序遍历用来确定左右子树

• 前，后序遍历用来确定左右子树的父节点，进而再带到中序序列中划分更小的左右子树

 

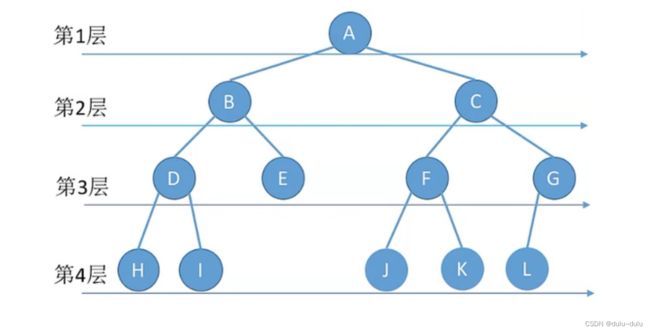
3.层次遍历

 所以层次遍历的结果为A,B,C,D,E,F,G,H,I,J,K,L

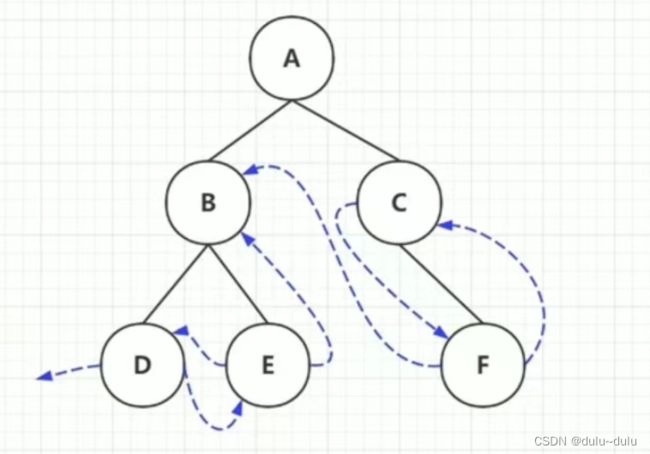
4.线索二叉树

如果要找某个节点的前驱和后继，那么必须完整地从根节点开始进行前，中，后遍历

 所以线索二叉树可以很直观地看出某个节点的前驱和后继

后序遍历：D,E,B,F,C,A

•从上到下，先找只有一个子节点的父节点，如图所示是C

•看线性表D,E,B,F,C,A,C的左侧为F，C指向F

•D没有左右子节点，看线性表D,E,B,F,C,A，D的左侧是空，D的右侧指向E

•以此类推，看E,F,可推出后序线索二叉树