C++ -- 红黑树封装set和map
文章目录
- 1. 红黑树概念和性质
-
- 1.1 概念
- 1.2 性质
- 1.3 实例
- 1.4 分析
- 2. 节点定义
- 3. 插入操作
- 4. 检测
- 5. 红黑树代码
- 6. 红黑树实现set和map
-
- 6.0 类设计图
- 6.1 红黑树包装复用
- 6.2 红黑树实现set
- 6.3 红黑树实现map
- 6.4 剖析代码
-
- 6.4.1 如何复用
- 6.4.2 如何区分set和map比较方式
- 6.4.3 set和map仿函数作用
- 6.4.4 怎么理解迭代器及其模板参数
- 6.4.5 迭代器中operator++()和operator--()
- 6.4.6 如何保证set的key值不能修改
- 6.4.7 如何保证map的key值不被修改value值可修改
- 6.4.8 怎么理解map中的operator[] ()
1. 红黑树概念和性质
1.1 概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍,因而是接近平衡的。
1.2 性质
- 每个节点要么是红色要么是黑色
- 整颗树的根节点是黑色
- 如果一个节点是红色,那么它的左右孩子节点是黑色
- 对每个节点,从该节点到其所有后代叶子节点的路径上均包含相同数目的黑色节点
- 每个叶子节点的左右空节点都是黑色
1.3 实例

1.4 分析
- 最短路径:路径上的节点全是黑色
- 最长路径:路径上的节点有黑色和红色
怎么保证最短路径的节点数目的两倍等于或者小于最长路径的节点数目?性质1-5来保证。
红黑树相比AVL树优势在哪里?AVL树需要旋转的树,红黑树不一定旋转(这样性能和AVL树差不多,但是红黑树更胜一筹),列举:

2. 节点定义
enum Color
{
RED,
BLACK
};
template
struct red_blackTreeNode
{
red_blackTreeNode* _left; //左节点指向
red_blackTreeNode* _right; //右节点指向
red_blackTreeNode* _parent; //父节点指向
pair _couple; //存储key/value
Color _color; //颜色标签
red_blackTreeNode(const pair& couple)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_couple(couple)
,_color(RED) //默认插入红色节点(插入红色节点才能保证对每个节点,从该节点到其所有后代叶子节点的路径上均包含相同数目的黑色节点)
};
3. 插入操作
- 根节点为空
- new节点,改变根指向,返回true
- 根节点不为空
- 找到插入位置
- 右查找:当前节点key值 < 插入节点key值
- 左查找:当前节点key值 > 插入节点key值
- 当前节点key值 = 插入节点key值 :直接返回false
- 在对应待插入位置插入
- new节点,当前插入位置指向该节点
- 右插入:当前节点key值 < 插入节点key值
- 左插入: 当前节点key值 > 插入节点key值
- 当前被插入节点父指针指向指向被连接节点
- 调整(TODO)
- 找到插入位置
如何调整?
- uncle存在且为红
- parent为红变黑
- grandpa为黑变红,uncle为红变黑
- 若grandpa_parent存在且为红,调整cur=grandpa,parent=grandpa_parent,grandpa=grandpa_parent->_parent,uncle=grandpa_parent -> _parent-> _left,调整后回到开始位置继续判断uncle是否存在且为红
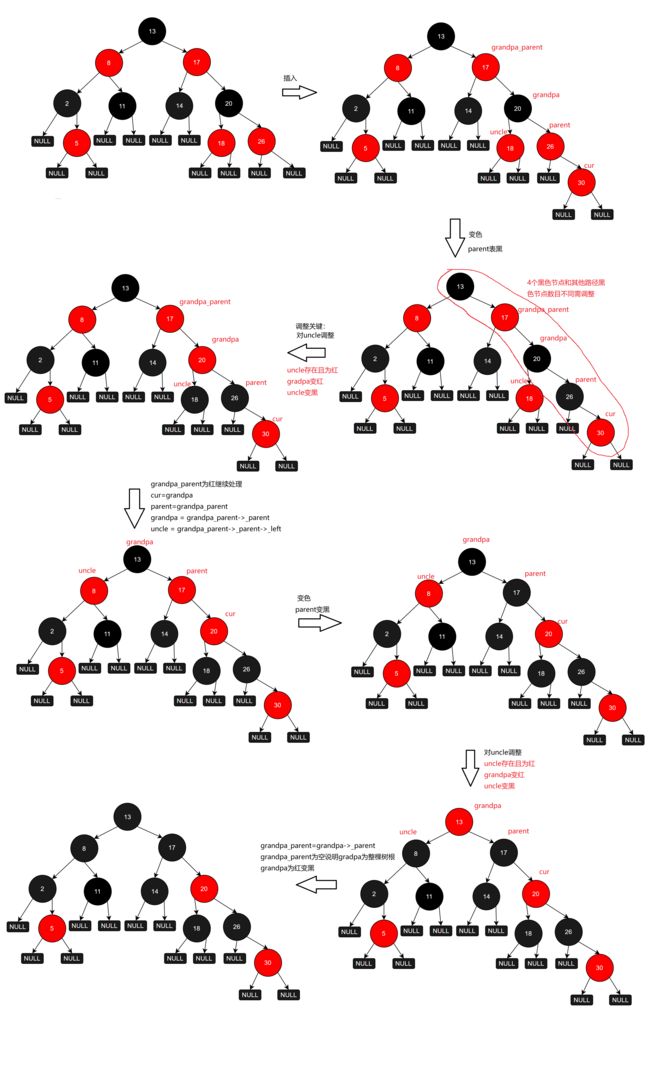
- uncle不存在时
- parent为红变黑
- 左低右高需旋转,grandpa为黑变红

抽象图
- 情况一:cur为红,parent为红,grandpa为黑,uncle存在且为红

解决方案:parent为红变黑,uncle为红变黑,grandpa为黑变红,如果grandpa的父节点是红色,则cur指向granda继续向上调整,如果grandpa的父节点是黑色,则停止调整。
- 情况二:cur为红,parent为红,grandpa为黑,uncle不存在/uncle存在且为黑

解决方案:左高右低采取右旋,左低右高采取左旋,parent为红变黑,grandpa为黑变红
- 情况三:cur为红,parent为红,grandpa为黑,uncle不存在/uncle存在且为黑

解决方案:先双旋(先左后右旋或者先后后左旋),最终cur变黑,grandpa变红
bool insert(const pair& couple)
{
if (_root == nullptr) //根为空:直接new并指向返回
{
_root = new node(couple);
return true;
}
/*找插入位置*/
node* parent = nullptr; //起初根节点的父节点为nullptr
node* cur = _root; //被插入节点指向
while (cur)
{
if (cur->_couple.first < couple.first) //右查找:当前节点key值 < 插入节点key值
{
parent = cur;
cur = cur->_right;
}
else if (cur->_couple.first > couple.first) //左查找: 当前节点key值 > 插入节点key值
{
parent = cur;
cur = cur->_left;
}
else //当前节点key值 = 插入节点key值:直接退出
{
return false;
}
}
/*在对应位置插入*/
cur = new node(couple);
if (parent->_couple.first > couple.first) //左插入: 当前节点key值 > 插入节点key值
{
parent->_left = cur;
}
else //右插入:当前节点key值 < 插入节点key值
{
parent->_right = cur;
}
cur->_parent = parent; //反向链接
/*调整*/
while (parent && parent->_color == RED)
{
node* grandpa = parent->_parent;
if (grandpa == nullptr)
{
break;
}
if (grandpa->_left == parent)
{
node* uncle = grandpa->_right;
if (uncle && uncle->_color == RED) //情况一:cur为红,parent为红,grandpa为黑,uncle存在且为红
{
parent->_color = BLACK;
uncle->_color = BLACK;
grandpa->_color = RED;
/*继续往上调整*/
cur = grandpa;
parent = cur->_parent;
}
else //情况二+三:cur为红,parent为红,grandpa为黑,uncle不存在/uncle存在且为黑
{
if (cur == parent->_left) //左高右低(右旋)
{
// grandpa
// / \
// parent uncle
// /
// cur
rightSingleRotate(grandpa); //grandpa为轴心右旋
parent->_color = BLACK;
grandpa->_color = RED;
}
else //
{
// grandpa
// / \
// parent uncle
// \
// cur
leftSingleRotate(parent); //parent为轴心左旋
rightSingleRotate(grandpa); //grandpa为轴心右旋
cur->_color = BLACK;
grandpa->_color = RED;
}
break;
}
}
else //grandpa->_left == parent
{
node* uncle = grandpa->_left;
if (uncle && uncle->_color == RED) //情况一:cur为红,parent为红,grandpa为黑,uncle存在且为红
{
parent->_color = BLACK;
uncle->_color = BLACK;
grandpa->_color = RED;
/*继续往上调整*/
cur = grandpa;
parent = cur->_parent;
}
else //情况二+三:cur为红,parent为红,grandpa为黑,uncle不存在/uncle存在且为黑
{
if (cur == parent->_right) //左高右低(左单旋)
{
// grandpa
// / \
// uncle parent
// \
// cur
leftSingleRotate(grandpa); //grandpa为轴心左旋
parent->_color = BLACK;
grandpa->_color = RED;
}
else //cur == parent->_left
{
// grandpa
// / \
// uncle parent
// /
// cur
rightSingleRotate(parent); //parent为轴心右旋
leftSingleRotate(grandpa); //grandpa为轴心左旋
cur->_color = BLACK;
grandpa->_color = RED;
}
break;
}
}
}
}
void leftSingleRotate(node* parent) //左单旋
{
//记录指针
node* parent_RightChild = parent->_right; //parent_RightChild = cur
node* parent_RightChild_LeftChild = parent_RightChild->_left; //parent_RightChild_LeftChild = curLeft
node* parent_parent = parent->_parent; //局部根或整棵树根的父节点
parent->_right = parent_RightChild_LeftChild; //让cur的左子树(curLeft)放在parent的右子树位置
if (parent_RightChild_LeftChild != nullptr) //H为0时,parent_RightChild_LeftChild=nullptr
{
parent_RightChild_LeftChild->_parent = parent; //curLeft的父节点指向指向parent
}
parent_RightChild->_left = parent; //让parent放在cur的左子树位置
parent->_parent = parent_RightChild; //parent的父节点指向指向cur
//cur(parent_RightChild)变为子树或者整颗树的根
if (parent_parent == nullptr) //parent是整颗树的根
{
_root = parent_RightChild; //cur(parent_RightChild)就是根
_root->_parent = nullptr;
}
else //parent是局部子树的根
{
if (parent_parent->_left == parent) //parent节点在父节点的左子树位置
{
parent_parent->_left = parent_RightChild;
}
else //parent节点在父节点的右子树位置
{
parent_parent->_right = parent_RightChild;
}
parent_RightChild->_parent = parent_parent; //cur(parent_RightChild)指向局部根的父节点
}
}
void rightSingleRotate(node* parent) //右单旋
{
//记录指针
node* parent_LeftChild = parent->_left; //parent_LeftChild = cur
node* parent_LeftChild_RightChild = parent_LeftChild->_right; //parent_LeftChild_RightChild = curRight
node* parent_parent = parent->_parent; //局部根或整棵树根的父节点
parent->_left = parent_LeftChild_RightChild; //让cur的右子树(curRight)放在parent的左子树位置
if (parent_LeftChild_RightChild != nullptr)
{
parent_LeftChild_RightChild->_parent = parent; //让curRight父节点的指向指向parent
}
parent_LeftChild->_right = parent; //让parent放在cur的右子树位置
parent->_parent = parent_LeftChild; //让parent的父节点指向指向cur
//cur(parent_LeftChild)变为子树或者整颗树的根
if (parent_parent == nullptr) //parent是整颗树的根
{
_root = parent_LeftChild; //cur(parent_LeftChild)就是根
_root->_parent = nullptr;
}
else //parent是局部子树的根
{
if (parent_parent->_left == parent) //parent节点在父节点的左子树位置
{
parent_parent->_left = parent_LeftChild;
}
else //parent节点在父节点的右子树位置
{
parent_parent->_right = parent_LeftChild;
}
parent_LeftChild->_parent = parent_parent; //cur(parent_LeftChild)指向局部根的父节点
}
}
4. 检测
void _inOrder(node* root) //中序遍历
{
if (root == nullptr)
{
return;
}
_inOrder(root->_left);
cout << root->_couple.first << " ";
_inOrder(root->_right);
}
int getreferenceValue(node* root)
{
node* cur = root;
int referenceValue = 0;
while (cur)
{
if (cur->_color == BLACK)
++referenceValue;
cur = cur->_left;
}
return referenceValue;
}
bool _checkoutRedRootParent(node* root) //检测红色节点的父节点是否为红
{
if (root == nullptr)
return true;
if (root->_color == RED
&& root->_parent
&& root->_parent->_color == RED) //红色节点一定有父节点
{
cout << "exist continuous RED root!" << endl;
return false;
}
return _checkoutRedRootParent(root->_left)
&& _checkoutRedRootParent(root->_right);
}
void _eachPathBlackRootNumber(node* root, int blackRootNumber, int& referenceValue)
{
if (root == nullptr)
{
if (blackRootNumber != referenceValue)
{
cout << "this path black root number is not equal!" << endl;
return;
}
return;
}
if (root->_color == BLACK)
++blackRootNumber;
_eachPathBlackRootNumber(root->_left, blackRootNumber, referenceValue);
_eachPathBlackRootNumber(root->_right, blackRootNumber, referenceValue);
}
int _heightDiffer(node* root)
{
if (root == nullptr)
return 0;
int leftHeight = _heightDiffer(root->_left);
int rightHeight = _heightDiffer(root->_right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
void inOrder()
{
_inOrder(_root);
cout << endl;
}
bool isBalance()
{
if (_root && _root->_color == RED) //整颗的根必须为黑
{
cout << "color of _root is RED!" << endl;
return false;
}
//如果一个节点是红色,那么它的左右孩子节点是黑色
if (!_checkoutRedRootParent(_root)) //检测红色节点的父节点是否为红
{
return false;
}
int referenceValue = getreferenceValue(_root); //求最左边路径的黑色节点数量作为参考值
//检测每条路径的黑色节点的数量
_eachPathBlackRootNumber(_root, 0, referenceValue);
return true;
}
int heightDiffer() //检测高度
{
return _heightDiffer(_root);
}
5. 红黑树代码
#pragma once
#include
#include
using namespace std;
enum Color
{
RED,
BLACK,
};
template
struct red_blackTreeNode
{
red_blackTreeNode* _left; //左节点指向
red_blackTreeNode* _right; //右节点指向
red_blackTreeNode* _parent; //父节点指向
pair _couple; //存储key/value
Color _color; //颜色标签
red_blackTreeNode(const pair& couple)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_couple(couple)
,_color(RED) //默认插入红色节点(插入红色节点才能保证对每个节点,从该节点到其所有后代叶子节点的路径上均包含相同数目的黑色节点)
{}
};
template
class red_blackTree
{
typedef red_blackTreeNode node;
public:
red_blackTree()
:_root(nullptr)
{}
node* find(const pair& key)
{
node* cur = _root;
while (cur)
{
if (cur->_couple.first < key)
cur = cur->_right;
else if (cur->_couple.first > key)
cur = cur->_left;
else
return cur;
}
return nullptr;
}
red_blackTree(const red_blackTree& tree) //拷贝构造(递归复制)
{
_root = _copy(tree._root);
}
bool insert(const pair& couple)
{
if (_root == nullptr) //根为空:直接new并指向返回
{
_root = new node(couple);
return true;
}
/*找插入位置*/
node* parent = nullptr; //起初根节点的父节点为nullptr
node* cur = _root; //被插入节点指向
while (cur)
{
if (cur->_couple.first < couple.first) //右查找:当前节点key值 < 插入节点key值
{
parent = cur;
cur = cur->_right;
}
else if (cur->_couple.first > couple.first) //左查找: 当前节点key值 > 插入节点key值
{
parent = cur;
cur = cur->_left;
}
else //当前节点key值 = 插入节点key值:直接退出
{
return false;
}
}
/*在对应位置插入*/
cur = new node(couple);
if (parent->_couple.first > couple.first) //左插入: 当前节点key值 > 插入节点key值
{
parent->_left = cur;
}
else //右插入:当前节点key值 < 插入节点key值
{
parent->_right = cur;
}
cur->_parent = parent; //反向链接
/*调整*/
while (parent && parent->_color == RED)
{
node* grandpa = parent->_parent;
if (grandpa == nullptr)
{
break;
}
if (grandpa->_left == parent)
{
node* uncle = grandpa->_right;
if (uncle && uncle->_color == RED) //情况一:cur为红,parent为红,grandpa为黑,uncle存在且为红
{
parent->_color = BLACK;
uncle->_color = BLACK;
grandpa->_color = RED;
/*继续往上调整*/
cur = grandpa;
parent = cur->_parent;
}
else //情况二+三:cur为红,parent为红,grandpa为黑,uncle不存在/uncle存在且为黑
{
if (cur == parent->_left) //左高右低(右旋)
{
// grandpa
// / \
// parent uncle
// /
// cur
rightSingleRotate(grandpa); //grandpa为轴心右旋
parent->_color = BLACK;
grandpa->_color = RED;
}
else //
{
// grandpa
// / \
// parent uncle
// \
// cur
leftSingleRotate(parent); //parent为轴心左旋
rightSingleRotate(grandpa); //grandpa为轴心右旋
cur->_color = BLACK;
grandpa->_color = RED;
}
break;
}
}
else //grandpa->_left == parent
{
node* uncle = grandpa->_left;
if (uncle && uncle->_color == RED) //情况一:cur为红,parent为红,grandpa为黑,uncle存在且为红
{
parent->_color = BLACK;
uncle->_color = BLACK;
grandpa->_color = RED;
/*继续往上调整*/
cur = grandpa;
parent = cur->_parent;
}
else //情况二+三:cur为红,parent为红,grandpa为黑,uncle不存在/uncle存在且为黑
{
if (cur == parent->_right) //左高右低(左单旋)
{
// grandpa
// / \
// uncle parent
// \
// cur
leftSingleRotate(grandpa); //grandpa为轴心左旋
parent->_color = BLACK;
grandpa->_color = RED;
}
else //cur == parent->_left
{
// grandpa
// / \
// uncle parent
// /
// cur
rightSingleRotate(parent); //parent为轴心右旋
leftSingleRotate(grandpa); //grandpa为轴心左旋
cur->_color = BLACK;
grandpa->_color = RED;
}
break;
}
}
}
_root->_color = BLACK; //整颗树的根为黑
return true; //插入成功
}
void inOrder()
{
_inOrder(_root);
cout << endl;
}
bool isBalance()
{
if (_root && _root->_color == RED) //整颗的根必须为黑
{
cout << "color of _root is RED!" << endl;
return false;
}
//如果一个节点是红色,那么它的左右孩子节点是黑色
if (!_checkoutRedRootParent(_root)) //检测红色节点的父节点是否为红
{
return false;
}
int referenceValue = getreferenceValue(_root); //求最左边路径的黑色节点数量作为参考值
//检测每条路径的黑色节点的数量
_eachPathBlackRootNumber(_root, 0, referenceValue);
return true;
}
int heightDiffer()
{
return _heightDiffer(_root);
}
~red_blackTree()
{
_destory(_root);
_root = nullptr;
}
private:
void leftSingleRotate(node* parent) //左单旋
{
//记录指针
node* parent_RightChild = parent->_right; //parent_RightChild = cur
node* parent_RightChild_LeftChild = parent_RightChild->_left; //parent_RightChild_LeftChild = curLeft
node* parent_parent = parent->_parent; //局部根或整棵树根的父节点
parent->_right = parent_RightChild_LeftChild; //让cur的左子树(curLeft)放在parent的右子树位置
if (parent_RightChild_LeftChild != nullptr) //H为0时,parent_RightChild_LeftChild=nullptr
{
parent_RightChild_LeftChild->_parent = parent; //curLeft的父节点指向指向parent
}
parent_RightChild->_left = parent; //让parent放在cur的左子树位置
parent->_parent = parent_RightChild; //parent的父节点指向指向cur
//cur(parent_RightChild)变为子树或者整颗树的根
if (parent_parent == nullptr) //parent是整颗树的根
{
_root = parent_RightChild; //cur(parent_RightChild)就是根
_root->_parent = nullptr;
}
else //parent是局部子树的根
{
if (parent_parent->_left == parent) //parent节点在父节点的左子树位置
{
parent_parent->_left = parent_RightChild;
}
else //parent节点在父节点的右子树位置
{
parent_parent->_right = parent_RightChild;
}
parent_RightChild->_parent = parent_parent; //cur(parent_RightChild)指向局部根的父节点
}
}
void rightSingleRotate(node* parent) //右单旋
{
//记录指针
node* parent_LeftChild = parent->_left; //parent_LeftChild = cur
node* parent_LeftChild_RightChild = parent_LeftChild->_right; //parent_LeftChild_RightChild = curRight
node* parent_parent = parent->_parent; //局部根或整棵树根的父节点
parent->_left = parent_LeftChild_RightChild; //让cur的右子树(curRight)放在parent的左子树位置
if (parent_LeftChild_RightChild != nullptr)
{
parent_LeftChild_RightChild->_parent = parent; //让curRight父节点的指向指向parent
}
parent_LeftChild->_right = parent; //让parent放在cur的右子树位置
parent->_parent = parent_LeftChild; //让parent的父节点指向指向cur
//cur(parent_LeftChild)变为子树或者整颗树的根
if (parent_parent == nullptr) //parent是整颗树的根
{
_root = parent_LeftChild; //cur(parent_LeftChild)就是根
_root->_parent = nullptr;
}
else //parent是局部子树的根
{
if (parent_parent->_left == parent) //parent节点在父节点的左子树位置
{
parent_parent->_left = parent_LeftChild;
}
else //parent节点在父节点的右子树位置
{
parent_parent->_right = parent_LeftChild;
}
parent_LeftChild->_parent = parent_parent; //cur(parent_LeftChild)指向局部根的父节点
}
}
node* _copy(node* root)
{
if (root == nullptr)
return nullptr;
node* copyTreeRoot = new node(root->_couple);
copyTreeRoot->_left = _copy(root->_left);
copyTreeRoot->_right = _copy(root->_right);
return copyTreeRoot;
}
void _inOrder(node* root) //中序遍历
{
if (root == nullptr)
{
return;
}
_inOrder(root->_left);
cout << root->_couple.first << " ";
_inOrder(root->_right);
}
int getreferenceValue(node* root)
{
node* cur = root;
int referenceValue = 0;
while (cur)
{
if (cur->_color == BLACK)
++referenceValue;
cur = cur->_left;
}
return referenceValue;
}
bool _checkoutRedRootParent(node* root) //检测红色节点的父节点是否为红
{
if (root == nullptr)
return true;
if (root->_color == RED
&& root->_parent
&& root->_parent->_color == RED) //红色节点一定有父节点
{
cout << "exist continuous RED root!" << endl;
return false;
}
return _checkoutRedRootParent(root->_left)
&& _checkoutRedRootParent(root->_right);
}
void _eachPathBlackRootNumber(node* root, int blackRootNumber, int& referenceValue)
{
if (root == nullptr)
{
if (blackRootNumber != referenceValue)
{
cout << "this path black root number is not equal!" << endl;
return;
}
return;
}
if (root->_color == BLACK)
++blackRootNumber;
_eachPathBlackRootNumber(root->_left, blackRootNumber, referenceValue);
_eachPathBlackRootNumber(root->_right, blackRootNumber, referenceValue);
}
int _heightDiffer(node* root)
{
if (root == nullptr)
return 0;
int leftHeight = _heightDiffer(root->_left);
int rightHeight = _heightDiffer(root->_right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
void _destory(node* root) //后序遍历销毁
{
if (root == nullptr)
return;
_destory(root->_left);
_destory(root->_right);
delete root;
}
private:
node* _root;
};
/*测试*/
void test_red_blackTree1()
{
//int arr[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
red_blackTree tree;
for (auto x : arr)
{
tree.insert(make_pair(x, x));
}
tree.inOrder(); //中序遍历(证明搜索二叉树)
red_blackTree copyTree(tree);
copyTree.inOrder();
cout << tree.isBalance() << endl; //判断是否为平衡树
}
void test_perfermance() //测试性能
{
srand(time(nullptr));
const size_t N = 1000000;
red_blackTree tree;
for (size_t i = 0; i < N; ++i)
{
size_t x = rand();
tree.insert(make_pair(x, x));
}
cout << tree.isBalance() << endl;
cout << tree.heightDiffer() << endl;
}
6. 红黑树实现set和map
6.0 类设计图

6.1 红黑树包装复用
#pragma once
#include
#include
using namespace std;
enum Color
{
RED,
BLACK,
};
/*采取复用:set --> T=KEY;map --> pair*/
template
struct red_blackTreeNode /*红黑树节点*/
{
red_blackTreeNode* _left; //左节点指向
red_blackTreeNode* _right; //右节点指向
red_blackTreeNode* _parent; //父节点指向
T _field; //存储key/value或者只存储key(字段)
Color _color; //颜色标签
red_blackTreeNode(const T& field)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
, _field(field)
,_color(RED) //默认插入红色节点(插入红色节点才能保证对每个节点,从该节点到其所有后代叶子节点的路径上均包含相同数目的黑色节点)
{}
};
template
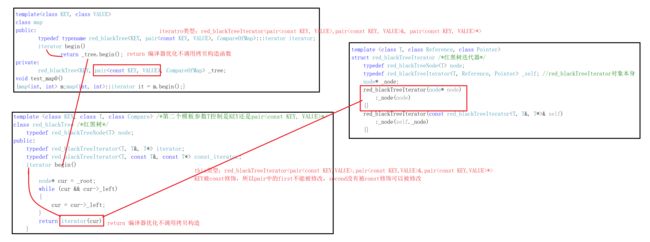
struct red_blackTreeIterator /*红黑树迭代器*/
{
typedef red_blackTreeNode node;
typedef red_blackTreeIterator _self; //red_blackTreeIterator对象本身
node* _node;
red_blackTreeIterator(node* node)
:_node(node)
{}
red_blackTreeIterator(const red_blackTreeIterator& self) /*满足隐式转换:iterator --> const_iterator*/
:_node(self._node)
{}
Reference operator*() //解引用获取key值
{
return _node->_field;
}
Pointer operator->() //取地址获取节点字段(field)地址
{
return &_node->_field;
}
bool operator!=(const _self& self) //节点不相等
{
return _node != self._node;
}
_self& operator++() //中序遍历(非递归)
{
if (_node->_right) //该节点右子树不为空,下一个节点就是该节点右子树最左节点
{
node* leftOfRightNode = _node->_right;
while (leftOfRightNode->_left)
{
leftOfRightNode = leftOfRightNode->_left;
}
_node = leftOfRightNode; //当前访问指向调整
}
else //右子树为空
{
node* cur = _node;
node* parent = cur->_parent;
while (parent && cur == parent->_right)
{
cur = parent;
parent = parent->_parent;
}
_node = parent; //当前访问指向调整
}
return *this;
}
_self& operator--() //反中序遍历(非递归)
{
if (_node->_left) //该节点左子树不为空,下一个节点就是该节点左子树最右节点
{
node* rightOfLeftNode = _node->_left;
while (rightOfLeftNode->_right)
{
rightOfLeftNode = rightOfLeftNode->_right;
}
_node = rightOfLeftNode; //当前访问指向调整
}
else //左子树为空
{
node* cur = _node;
node* parent = cur->_parent;
while (parent && cur == parent->_left)
{
cur = parent;
parent = parent->_parent;
}
_node = parent; //当前访问指向调整
}
return *this;
}
};
template /*第二个模板参数T控制是KEY还是pair*/
class red_blackTree /*红黑树*/
{
typedef red_blackTreeNode node;
public:
typedef red_blackTreeIterator iterator;
typedef red_blackTreeIterator const_iterator;
public:
red_blackTree()
:_root(nullptr)
{}
/*迭代器操作*/
iterator begin()
{
node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}
iterator end()
{
return iterator(nullptr);
}
const_iterator begin() const
{
node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return const_iterator(cur);
}
const_iterator end() const
{
return const_iterator(nullptr);
}
node* find(const T& key)
{
Compare compare;
node* cur = _root;
while (cur)
{
if (compare(cur->_field) < compare(key))
cur = cur->_right;
else if (compare(cur->_field) > compare(key))
cur = cur->_left;
else
return cur;
}
return nullptr;
}
red_blackTree(const red_blackTree& tree) //拷贝构造(递归复制)
{
_root = _copy(tree._root);
}
pair Insert(const T& field)
{
Compare compare;
if (_root == nullptr) //根为空:直接new并指向返回
{
_root = new node(field);
return make_pair(iterator(_root), true);
}
/*找插入位置*/
node* parent = nullptr; //起初根节点的父节点为nullptr
node* cur = _root; //被插入节点指向
while (cur)
{
if (compare(cur->_field) < compare(field)) //右查找:当前节点key值 < 插入节点key值
{
parent = cur;
cur = cur->_right;
}
else if (compare(cur->_field) > compare(field)) //左查找: 当前节点key值 > 插入节点key值
{
parent = cur;
cur = cur->_left;
}
else //当前节点key值 = 插入节点key值:直接退出
{
return make_pair(iterator(cur), false);
}
}
/*在对应位置插入*/
cur = new node(field);
node* newnode = cur;
if (compare(parent->_field) > compare(field)) //左插入: 当前节点key值 > 插入节点key值
{
parent->_left = cur;
}
else //右插入:当前节点key值 < 插入节点key值
{
parent->_right = cur;
}
cur->_parent = parent; //反向链接
/*调整*/
while (parent && parent->_color == RED)
{
node* grandpa = parent->_parent;
if (grandpa == nullptr)
{
break;
}
if (grandpa->_left == parent)
{
node* uncle = grandpa->_right;
if (uncle && uncle->_color == RED) //情况一:cur为红,parent为红,grandpa为黑,uncle存在且为红
{
parent->_color = BLACK;
uncle->_color = BLACK;
grandpa->_color = RED;
/*继续往上调整*/
cur = grandpa;
parent = cur->_parent;
}
else //情况二+三:cur为红,parent为红,grandpa为黑,uncle不存在/uncle存在且为黑
{
if (cur == parent->_left) //左高右低(右旋)
{
// grandpa
// / \
// parent uncle
// /
// cur
rightSingleRotate(grandpa); //grandpa为轴心右旋
parent->_color = BLACK;
grandpa->_color = RED;
}
else //
{
// grandpa
// / \
// parent uncle
// \
// cur
leftSingleRotate(parent); //parent为轴心左旋
rightSingleRotate(grandpa); //grandpa为轴心右旋
cur->_color = BLACK;
grandpa->_color = RED;
}
break;
}
}
else //grandpa->_left == parent
{
node* uncle = grandpa->_left;
if (uncle && uncle->_color == RED) //情况一:cur为红,parent为红,grandpa为黑,uncle存在且为红
{
parent->_color = BLACK;
uncle->_color = BLACK;
grandpa->_color = RED;
/*继续往上调整*/
cur = grandpa;
parent = cur->_parent;
}
else //情况二+三:cur为红,parent为红,grandpa为黑,uncle不存在/uncle存在且为黑
{
if (cur == parent->_right) //左高右低(左单旋)
{
// grandpa
// / \
// uncle parent
// \
// cur
leftSingleRotate(grandpa); //grandpa为轴心左旋
parent->_color = BLACK;
grandpa->_color = RED;
}
else //cur == parent->_left
{
// grandpa
// / \
// uncle parent
// /
// cur
rightSingleRotate(parent); //parent为轴心右旋
leftSingleRotate(grandpa); //grandpa为轴心左旋
cur->_color = BLACK;
grandpa->_color = RED;
}
break;
}
}
}
_root->_color = BLACK; //整颗树的根为黑
return make_pair(iterator(newnode), true); //插入成功
}
~red_blackTree()
{
_destory(_root);
_root = nullptr;
}
private:
void leftSingleRotate(node* parent) //左单旋
{
//记录指针
node* parent_RightChild = parent->_right; //parent_RightChild = cur
node* parent_RightChild_LeftChild = parent_RightChild->_left; //parent_RightChild_LeftChild = curLeft
node* parent_parent = parent->_parent; //局部根或整棵树根的父节点
parent->_right = parent_RightChild_LeftChild; //让cur的左子树(curLeft)放在parent的右子树位置
if (parent_RightChild_LeftChild != nullptr) //H为0时,parent_RightChild_LeftChild=nullptr
{
parent_RightChild_LeftChild->_parent = parent; //curLeft的父节点指向指向parent
}
parent_RightChild->_left = parent; //让parent放在cur的左子树位置
parent->_parent = parent_RightChild; //parent的父节点指向指向cur
//cur(parent_RightChild)变为子树或者整颗树的根
if (parent_parent == nullptr) //parent是整颗树的根
{
_root = parent_RightChild; //cur(parent_RightChild)就是根
_root->_parent = nullptr;
}
else //parent是局部子树的根
{
if (parent_parent->_left == parent) //parent节点在父节点的左子树位置
{
parent_parent->_left = parent_RightChild;
}
else //parent节点在父节点的右子树位置
{
parent_parent->_right = parent_RightChild;
}
parent_RightChild->_parent = parent_parent; //cur(parent_RightChild)指向局部根的父节点
}
}
void rightSingleRotate(node* parent) //右单旋
{
//记录指针
node* parent_LeftChild = parent->_left; //parent_LeftChild = cur
node* parent_LeftChild_RightChild = parent_LeftChild->_right; //parent_LeftChild_RightChild = curRight
node* parent_parent = parent->_parent; //局部根或整棵树根的父节点
parent->_left = parent_LeftChild_RightChild; //让cur的右子树(curRight)放在parent的左子树位置
if (parent_LeftChild_RightChild != nullptr)
{
parent_LeftChild_RightChild->_parent = parent; //让curRight父节点的指向指向parent
}
parent_LeftChild->_right = parent; //让parent放在cur的右子树位置
parent->_parent = parent_LeftChild; //让parent的父节点指向指向cur
//cur(parent_LeftChild)变为子树或者整颗树的根
if (parent_parent == nullptr) //parent是整颗树的根
{
_root = parent_LeftChild; //cur(parent_LeftChild)就是根
_root->_parent = nullptr;
}
else //parent是局部子树的根
{
if (parent_parent->_left == parent) //parent节点在父节点的左子树位置
{
parent_parent->_left = parent_LeftChild;
}
else //parent节点在父节点的右子树位置
{
parent_parent->_right = parent_LeftChild;
}
parent_LeftChild->_parent = parent_parent; //cur(parent_LeftChild)指向局部根的父节点
}
}
node* _copy(node* root)
{
if (root == nullptr)
return nullptr;
node* copyTreeRoot = new node(root->_couple);
copyTreeRoot->_left = _copy(root->_left);
copyTreeRoot->_right = _copy(root->_right);
return copyTreeRoot;
}
void _destory(node* root) //后序遍历销毁
{
if (root == nullptr)
return;
_destory(root->_left);
_destory(root->_right);
delete root;
}
private:
node* _root;
};
6.2 红黑树实现set
#pragma once
#include "red_blackTree.h"
namespace my_set
{
template
class set
{
struct CompareOfSet
{
const KEY& operator()(const KEY& key) /*仿函数作用:取值做比较*/
{
return key;
}
};
public:
//typedef typename red_blackTree::iterator iterator; /*NO*/
typedef typename red_blackTree::const_iterator iterator;
typedef typename red_blackTree::const_iterator const_iterator;
iterator begin()
{
return _tree.begin();
}
iterator end()
{
return _tree.end();
}
pair insert(const KEY& field)
{
return _tree.Insert(field);
}
private:
red_blackTree _tree;
};
void test_set()
{
int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
set s;
for (auto x : arr)
{
s.insert(x);
}
set::iterator it = s.begin();
while (it != s.end())
{
cout << *it << " ";
++it;
}
cout << endl;
}
}
6.3 红黑树实现map
#pragma once
#include "red_blackTree.h"
namespace my_map
{
template
class map
{
struct CompareOfMap
{
const KEY& operator()(const pair& couple) /*仿函数作用:取值做比较*/
{
return couple.first;
}
};
public:
typedef typename red_blackTree, CompareOfMap>::iterator iterator;
iterator begin()
{
return _tree.begin();
}
iterator end()
{
return _tree.end();
}
pair insert(const pair& field)
{
return _tree.Insert(field);
}
VALUE& operator[](const KEY& key)
{
pair ret = insert(make_pair(key, VALUE()));
return ret.first->second;
}
private:
red_blackTree, CompareOfMap> _tree;
};
void test_map1()
{
map dict;
dict.insert(make_pair("melon", "西瓜"));
dict.insert(make_pair("strawberry", "草莓"));
dict.insert(make_pair("pineapple", "菠萝"));
dict.insert(make_pair("lemon", "柠檬"));
dict.insert(make_pair("orange", "橘子"));
map::iterator it = dict.begin();
while (it != dict.end())
{
cout << it->first << ":" << it->second << endl;
++it;
}
cout << endl;
//for (auto& x : dict)
//{
// cout << x.first << ":" << x.second << endl;
//}
//cout << endl;
}
void test_map2()
{
std::string arr[] = { "西瓜", "西瓜", "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "香蕉", "苹果", "香蕉", "梨子", "梨子"};
map countMap;
for (auto& x : arr)
{
countMap[x]++;
}
for (auto& x : countMap)
{
cout << x.first << ":" << x.second << endl;
}
cout << endl;
}
}
6.4 剖析代码
6.4.1 如何复用
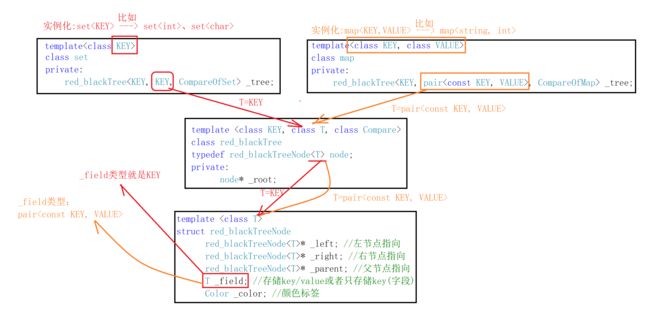
6.4.2 如何区分set和map比较方式
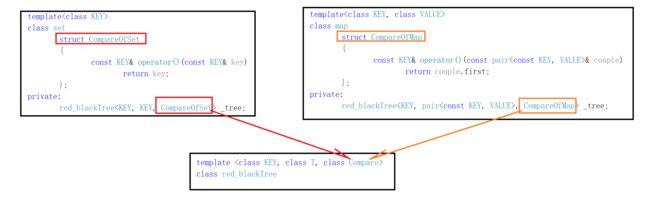
6.4.3 set和map仿函数作用

6.4.4 怎么理解迭代器及其模板参数

6.4.5 迭代器中operator++()和operator–()

//++操作:右子树为空,回到parent->_left = cur的parent的位置,右子树不为空,走到右子树的最左节点
//--操作:相反,左子树为空,回到parent->_right = cur的parent的位置,左子树不为空,走到左子树的最右节点
_self& operator++() //中序遍历(非递归)
{
if (_node->_right) //该节点右子树不为空,下一个节点就是该节点右子树最左节点
{
node* leftOfRightNode = _node->_right;
while (leftOfRightNode->_left)
{
leftOfRightNode = leftOfRightNode->_left;
}
_node = leftOfRightNode; //当前访问指向调整
}
else //右子树为空
{
node* cur = _node;
node* parent = cur->_parent;
while (parent && cur == parent->_right)
{
cur = parent;
parent = parent->_parent;
}
_node = parent; //当前访问指向调整
}
return *this;
}
_self& operator--() //反中序遍历(非递归)
{
if (_node->_left) //该节点左子树不为空,下一个节点就是该节点左子树最右节点
{
node* rightOfLeftNode = _node->_left;
while (rightOfLeftNode->_right)
{
rightOfLeftNode = rightOfLeftNode->_right;
}
_node = rightOfLeftNode; //当前访问指向调整
}
else //左子树为空
{
node* cur = _node;
node* parent = cur->_parent;
while (parent && cur == parent->_left)
{
cur = parent;
parent = parent->_parent;
}
_node = parent; //当前访问指向调整
}
return *this;
}
6.4.6 如何保证set的key值不能修改

6.4.7 如何保证map的key值不被修改value值可修改
6.4.8 怎么理解map中的operator[] ()
