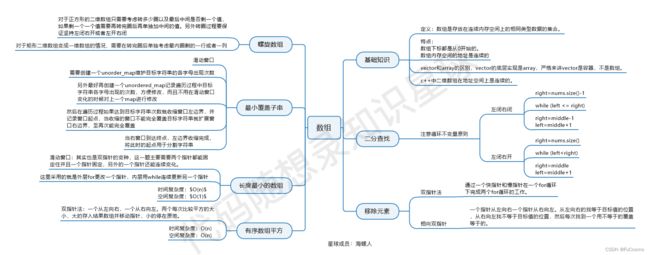
代码随想录算法训练营第二天| 977.有序数组的平方、209.长度最小的子数组（ACM模式）

977.有序数组的平方

文档讲解 ： 代码随想录 - 977.有序数组的平方
状态：再次回顾。

双指针法入门经典题目
首先得明确的是，题目的数组是有序的，并且存在负数。
那么：
平方后的最大值，要不就是数组最后一个数，要不就是第一个数，不可能是中间的数。

两个数形成比较或者存在关系，并且位于首尾两端，很容易想起双指针法。

本题双指针法图解：

本题代码（ACM)

#include 
#include 
using namespace std;

vector<int> sortedSquares(vector<int>& nums) {
	int i = 0;
	int j = nums.size() - 1; //定义双指针，分别指向最小值和最大值（在非递减顺序排序数组中）
	vector<int> result(nums.size()); //定义结果数组
	for (int index = result.size() - 1; index >= 0; index--) {
		if (nums[i] * nums[i] < nums[j] * nums[j]) { //如果最大值平方比最小值平方大，取最大值平方，并且右指针左移
			result[index] = nums[j] * nums[j];
			j--;
		}
		else { //如果最大值平方比最小值平方小或者相等，取最小值平方，并且左指针右移
			result[index] = nums[i] * nums[i];
			i++;
		}
	}
	return result;
}

int main() {
	/*
		输入描述：
		第一行一个整数，表示数组长度；
		第二行n个整数，表示数组内元素，注：数组内数字必须按非递减顺序排序，可为负数；
	*/
	int n;
	cin >> n;
	vector<int> nums(n);
	for (int i = 0; i < n; i++) cin >> nums[i];

	vector<int> newSquares = sortedSquares(nums);
	cout << "[";
	for (int i = 0; i < newSquares.size() - 1; i++) {
		cout << newSquares[i] << ",";
	}
	cout << newSquares[newSquares.size() - 1] << "]";
	return 0;
}

209.长度最小的子数组

文档讲解 ： 代码随想录 - 209.长度最小的子数组
状态：再次回顾。

滑动窗口法经典题目
滑动窗口题目关键词：找出满足条件长度最小连续子数组（串）

滑动窗口：不断地调节子序列的起始位置和终止位置，从而得出想要结果

滑动窗口其实也是双指针法的应用，其中左指针表示滑动窗口起始位置，右指针表示滑动窗口终止位置，右指针一般起到循环索引的作用，也就意味着，如果一个for循环，当右指针到循环终止条件时，循环结束。

本题查找过程：

本题代码（ACM)

#include 
#include 
#include 
using namespace std;

int minSubArrayLen(int target, vector<int>& nums) {
	int minLen = INT_MAX; // 定义连续子数组最小值
	int i = 0; // 滑动窗口起始位置
	int j = 0; // 滑动窗口终止位置
	int sum = 0; // 用于统计连续子数组和并和target进行比较
	for (; j < nums.size(); j++) { // 终止位置移动
		sum += nums[j];
		while (sum >= target) { // 当和满足条件时
			minLen = min(minLen, j - i + 1); // 记录最小长度
			sum -= nums[i]; // 开始滑动窗口
			i++; // 起始位置移动
		}
	}
	return minLen == INT_MAX ? 0 : minLen;
}

int main() {
	/*
		输入描述：
		第一行一个正整数，表示数组长度n
		第二行n个正整数，表示正整数数组内元素
		第三行一个正整数，表示条件值target
	*/
	int n;
	cin >> n;
	vector<int> nums(n);
	int target;
	for (int i = 0; i < n; i++) cin >> nums[i];
	cin >> target;

	cout << minSubArrayLen(target, nums) << endl;
	return 0;
}

59.螺旋矩阵II

文档讲解 ： 代码随想录 - 59.螺旋矩阵II
状态：再次回顾。存在问题：忘了注意边界条件，导致边界条件报错。

和二分法类似，注意边界条件，以及坚持循环不变量原则

模拟顺时针画矩阵的过程:

• 填充上行从左到右
• 填充右列从上到下
• 填充下行从右到左
• 填充左列从下到上

这题可以坚持左闭右开原则，画4×4矩阵如图：

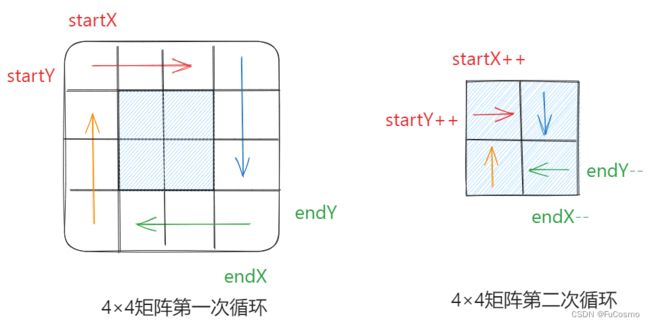
本题代码（ACM)

#include 
#include 
using namespace std;

vector<vector<int>> generateMatrix(int n) {
	int startX = 0; int endX = n - 1; // 定义第一列和最后一列
	int startY = 0; int endY = n - 1; // 定义第一行和最后一行
	int index = n / 2; // 定义画矩阵的圈数
	int count = 1; // 计数
	vector<vector<int>> result(n, vector<int>(n)); //结果数组
	while (index--) {
		for (int i = startX; i < endX; i++) {
			result[startY][i] = count++;
		}
		for (int i = startY; i < endY; i++) {
			result[i][endX] = count++;
		}
		for (int i = endX; i > startX; i--) {
			result[endY][i] = count++;
		}
		for (int i = endY; i > startY; i--) {
			result[i][startX] = count++;
		}
		startX++; endX--;
		startY++; endY--;
	}
	if (n % 2) {
		result[n / 2][n / 2] = count;
	}
	return result;
}

int main() {
	/*
		输入描述：输入一个正整数n
	*/
	int n;
	cin >> n;

	vector<vector<int>> resultMatrix = generateMatrix(n);
	cout << "[";
	for (int i = 0; i < n - 1; i++) {
		cout << "[";
		for (int j = 0; j < n - 1; j++) {
			cout << resultMatrix[i][j] << ",";
		}
		cout << resultMatrix[i][n - 1] << "],";
	}
	cout << "[";
	for (int j = 0; j < n - 1; j++) {
		cout << resultMatrix[n - 1][j] << ",";
	}
	cout << resultMatrix[n - 1][n - 1] << "]]";
	return 0;
}

总结

文档讲解 ： 代码随想录 - 总结
状态：再次回顾。

数组理论基础

记录重点

1. 数组是存放在连续内存空间上的相同类型数据的集合。
2. 数组具有连续性，在内存空间的地址是连续的 --> 删除或者增添元素的时候，得移动其他元素地址
3. 数组下标都是从0开始的。
4. 数组内存空间的地址是连续的。

二分法

二分法前提条件

1. 有序数组
2. 数组中无重复元素 （因为一旦有重复元素，使用二分法返回的元素下标可能不是唯一的。）

二分法重点
想清楚区间定义，保持区间不变量

双指针法

双指针法（快慢指针法）：通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
定义快慢指针

• 快指针：寻找新数组的元素，新数组就是不含有目标元素的数组
• 慢指针：指向更新，更新新数组下标的位置

两个数形成比较或者存在关系，并且位于首尾两端，很容易想起双指针法。

其他知识

• 数组在内存中是连续的地址空间，不能释放单一元素，如果要释放，就是全释放（程序运行结束，回收内存栈空间）。
• C++中vector和array的区别一定要弄清楚，vector的底层实现是array，封装后使用更友好。

滑动窗口

滑动窗口题目关键词：找出满足条件长度最小连续子数组（串）

滑动窗口：不断地调节子序列的起始位置和终止位置，从而得出想要结果

滑动窗口其实也是双指针法的应用，其中左指针表示滑动窗口起始位置，右指针表示滑动窗口终止位置，右指针一般起到循环索引的作用，也就意味着，如果一个for循环，当右指针到循环终止条件时，循环结束。

滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。

模拟行为

和二分法类似，注意边界条件，以及坚持循环不变量原则

总结