二分查找--图文详解

1. 什么是二分查找

二分查找也称折半查找，是在一组有序(升序/降序)的数据中查找一个元素，它是一种效率较高的查找方法。

2. 原理

1. 查找的目标数据元素必须是有序的。没有顺序的数据，二分法就失去意义。
2. 数据元素通常是数值型，可以比较大小。
3. 将目标元素和查找范围的中间值做比较（如果目标元素=中间值，查找结束），将目标元素分到较大/或者较小的一组。
4. 通过分组，可以将查找范围缩小一半。
5. 重复第三步，直到目标元素=新的范围的中间值，查找结束。

3. 例子

(本文以升序为例进行讲解，降序方法类似）

3.1 当数组长度为奇数

假设有一组数据{1,2,3,4,5,6,7}

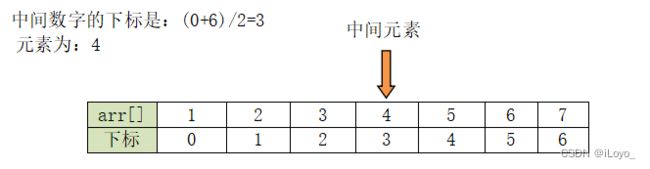
是奇数的情况很简单，指向中间的数字也很容易理解

如果要查找的数字是6，因为6大于中间的数字(4)，所以舍去左边的数据。

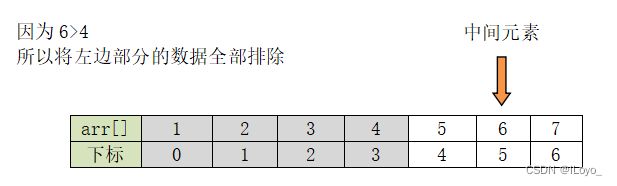
3.1 当数组长度为偶数

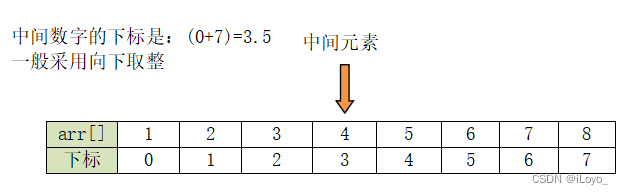
当取中间元素，遇到两边数据个数不同时，并不影响我们查找元素，只需要规定是向上或向下取整。

所以数组长度是偶数还是奇数这个并不重要，也不影响怎么排除的问题，无非是多排除一个数字或者少排除一个数字。

3.3 实现过程

在 {1,2,3,4,5,6,7,8,9,10} 中查找元素9。

第一步要找到中间元素，设置两个变量low、high，分别指向数组第一个元素下标和最后一个元素下标，从而控制数组的范围，再根据low和high确定中间元素的下标mid

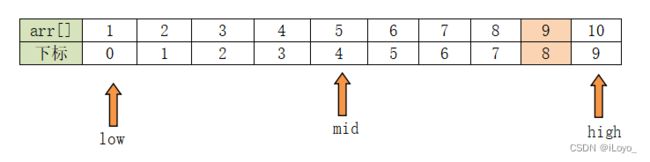
根据mid锁定的元素，和查找的元素(9)比较，确定新的查找范围、low 和high

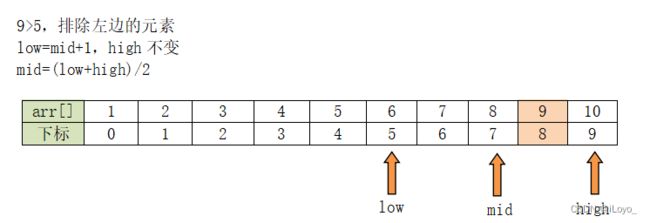
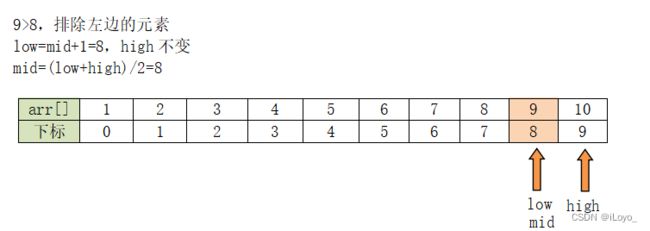
此时，mid=8,arr[mid]=9，与要查找的元素相同，即已经找到了，并返回其下标。

如果数组中没有要查找的元素，会出现什么情况呢？

假设我们上面要查找的元素是：11

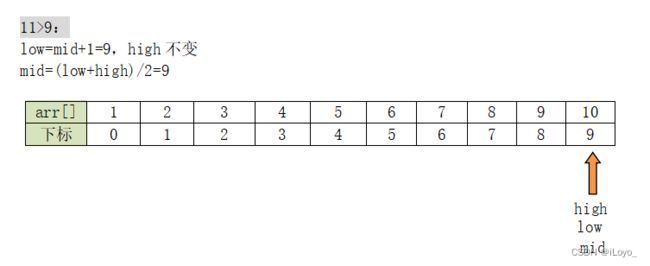
此时low=high=mid=9，arr[mid]=10不等于11，查找了整个数组都没有找到。

根据上述过程编写代码：

定义所需变量：

	int arr[10] = {1,2,3,4,5,6,7,8,9,10};//定义一个初始数组
	int n;//被查找的数
	printf("请输入你要查找的数:");
	scanf("%d", &n);//输入
	int len = sizeof(arr)/sizeof(arr[0]);//计算数组长度
	int low = 0;
	int high=len-1;//数组最后一个元素的下标
	int mid=(low+high)/2;//中间元素的下标

查找过程中，low一直在high的左边，即low

我们用while循环语句控制查找过程
while语句的用法

	while (low <= high)//循环结束条件
	{
		//确定数组范围
		mid = (low + high) / 2;
		if (arr[mid] == n)
		{
			printf("找到了，下标是：%d\n", mid);
			break;
		}
		else if (arr[mid] > n)
		{
			high = mid -1;
		}
		else 
		{
			low = mid + 1;
		}
	}

完整代码：

#include
int main()
{
	int arr[10] = {1,2,3,4,5,6,7,8,9,10};
	int n;
	printf("请输入你要查找的数:");
	scanf("%d", &n);
	int len = sizeof(arr)/sizeof(arr[0]);
	int low = 0;
	int high=len-1;
	int mid=(low+high)/2;
	while (low <= high)
	{
		mid = (low + high) / 2;
		if (arr[mid] == n)
		{
			printf("找到了，下标是：%d\n", mid);
			break;
		}
		else if (arr[mid] > n)
		{
			high = mid -1;
		}
		else 
		{
			low = mid + 1;
		}
	}
	if (low > high)
		printf("没找到");
	return 0;
}

降序排列的数组进行二分查找时，只需改变判断条件：

else if (arr[mid] < n)
		{
			high = mid - 1;
		}

4. 顺序查找与二分查找的区别

对数组{1,2,3,4,5,6,7,8,9,10}进行顺序查找：

//在一个有序数组中查找具体的某个数字n
#include
int main()
{
	int arr[10] = { 1,2,3,4,5,6,7,8,9,10 };//升序
	int n;
	scanf("%d", &n);
	int i;
	for (i = 0; i < 10; i++)
	{
		if (arr[i] == n)
		{
			printf("找到了，下标是：%d\n", i);
			break;
		}
	}
	if (i == 10)
	{
		printf("没找到\n");
	}
	return 0;
}

虽然顺序查找法在书写上比二分法查找要简洁，但二分法比顺序查找速度更快

两者在查找前，必须知道将要查找的“值”

查找目的都是该“值”在列表中所在的位置(下标)

注：数据量越大，越能体现出二分法的快速性；相反数据量小的话，两者都可以使用

---

结束语

掌握了二分法的思想，代码实现就变得简单了。从hello world，到这里，你只要肯付出，就会有回报，加油！
　　早起的鸟儿有虫吃。
　　我们下一篇文章再见。