梅涅劳斯定理和塞瓦定理
图库: link
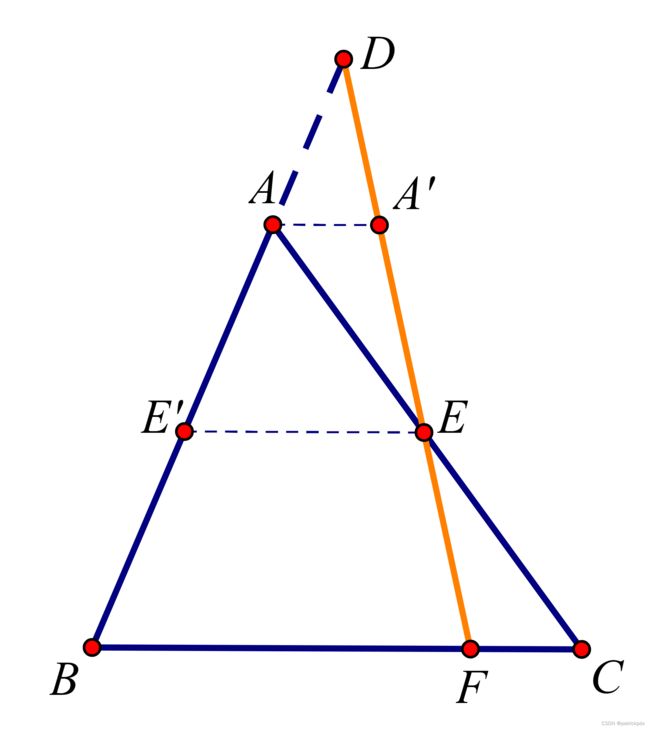
梅涅劳斯定理
证明:
过 A A A 和 E E E 分别作 B C BC BC 的平行线, 分别交 D E F DEF DEF, A B AB AB 所在直线于 A ′ A' A′, E ′ E' E′.
将所有比值都转换为 A A ′ AA' AA′, E E ′ EE' EE′, B F BF BF, F C FC FC 之间的比值: E C / E A = F C / A A ′ EC/EA=FC/AA' EC/EA=FC/AA′, A D / B D = A A ′ / B F AD/BD=AA'/BF AD/BD=AA′/BF, 进而命题得证.
(过 D D D 作 B C BC BC 的平行线交 A C AC AC 所在直线于 D ′ D' D′, 也可证得此命题.)
推论1. 分别作直线 A D AD AD, C F CF CF, B E BE BE 关于 ∠ A \angle A ∠A, ∠ C \angle C ∠C, ∠ B \angle B ∠B 的对称直线, 分别与 B C BC BC, A B AB AB, A C AC AC 交于 D ′ D' D′, F ′ F' F′, E ′ E' E′, 则此三点亦共线.
对于 △ A B C \triangle ABC △ABC 和截线 D ′ , E ′ , F ′ D', E', F' D′,E′,F′,
sin ∠ D ′ A B sin ∠ D ′ A C sin ∠ E ′ B C sin ∠ A B C sin ∠ A C F ′ sin ∠ A C B = sin C A D sin B A D sin A B E sin C B E sin B C F sin A C F \frac{\sin \angle D'AB}{\sin \angle D'AC} \frac{\sin\angle E'BC}{\sin\angle ABC} \frac{\sin\angle ACF'}{\sin\angle ACB} = \frac{\sin CAD }{\sin BAD} \frac{\sin ABE}{\sin CBE} \frac{\sin BCF}{\sin ACF} sin∠D′ACsin∠D′ABsin∠ABCsin∠E′BCsin∠ACBsin∠ACF′=sinBADsinCADsinCBEsinABEsinACFsinBCF
对于 △ A B C \triangle ABC △ABC 和截线 D , E , F D, E, F D,E,F, 应用梅涅劳斯定理可知后者等于1.
应用梅涅劳斯定理第一角元形式逆定理可知三点共线.
推论2. △ A B C \triangle ABC △ABC 的三个外角平分线分别和对边相交, 所得的三个点共线.
证明: 对于 △ A B C \triangle ABC △ABC 和 F , E , D F, E, D F,E,D,
sin ∠ F B A sin ∠ F B C sin ∠ C A D sin ∠ B A D sin ∠ B C E sin ∠ A C E = sin ( π / 2 − B / 2 ) sin ( π / 2 + B / 2 ) sin ( π / 2 − A / 2 ) sin ( π / 2 + A / 2 ) sin ( π / 2 + C / 2 ) sin ( π / 2 − C / 2 ) = 1 \frac{\sin \angle FBA}{\sin \angle FBC} \frac{\sin\angle CAD}{\sin\angle BAD} \frac{\sin\angle BCE}{\sin\angle ACE} = \frac{\sin (\pi/2-B/2) }{\sin (\pi/2+B/2)} \frac{\sin (\pi/2-A/2)}{\sin (\pi/2 + A/2)} \frac{\sin (\pi/2+C/2)}{\sin (\pi/2-C/2)} = 1 sin∠FBCsin∠FBAsin∠BADsin∠CADsin∠ACEsin∠BCE=sin(π/2+B/2)sin(π/2−B/2)sin(π/2+A/2)sin(π/2−A/2)sin(π/2−C/2)sin(π/2+C/2)=1
应用梅涅劳斯定理第一角元形式逆定理可知三点共线.
推论3. △ A B C \triangle ABC △ABC 的三个顶点作其外接圆的切线, 分别和对边相交, 所得的三个点共线.
对于 △ A B C \triangle ABC △ABC 和截线 A 1 B 1 C 1 A_1 B_1 C_1 A1B1C1,
sin ∠ A 1 A B sin ∠ A 1 A C sin ∠ B 1 B C sin ∠ B 1 B A sin ∠ C 1 C A sin ∠ C 1 C B = sin C sin B sin A sin C sin B sin A = 1 \frac{\sin \angle A_1AB}{\sin \angle A_1AC} \frac{\sin\angle B_1BC}{\sin\angle B_1BA} \frac{\sin\angle C_1CA}{\sin\angle C_1CB} = \frac{\sin C }{\sin B} \frac{\sin A}{\sin C} \frac{\sin B}{\sin A} = 1 sin∠A1ACsin∠A1ABsin∠B1BAsin∠B1BCsin∠C1CBsin∠C1CA=sinBsinCsinCsinAsinAsinB=1
应用梅涅劳斯定理第一角元形式逆定理可知三点共线.
推论4. 若 ∠ A 1 P B = ∠ A P B 1 \angle A_{1}PB= \angle APB_{1} ∠A1PB=∠APB1, 则 ∠ A 1 P C = ∠ A P C 1 \angle A_{1}PC= \angle APC_{1} ∠A1PC=∠APC1, ∠ B P C 1 = ∠ C P B 1 \angle BPC_{1}= \angle CPB_{1} ∠BPC1=∠CPB1.
推论5. 如图, 已知 ⨀ O 1 \bigodot O_{1} ⨀O1, ⨀ O 2 \bigodot O_{2} ⨀O2, ⨀ O 3 \bigodot O_{3} ⨀O3 为 △ A B C \triangle ABC △ABC 旁切圆, A 1 A_{1} A1, A 2 A_{2} A2, B 1 B_{1} B1, B 2 B_{2} B2 C 1 C_{1} C1, C 2 C_{2} C2, 分别为切点, A 3 A_{3} A3, B 3 B_{3} B3, C 3 C_{3} C3 为三条切点弦所在直线与旁切圆所切的边所在直线的交点, 三条切点弦所在直线交出 P 1 P_1 P1, P 2 P_2 P2, P 3 P_3 P3 三点. (1) P 1 A P_{1}A P1A, P 2 B P_{2}B P2B, P 3 C P_{3}C P3C 分别垂直于 B C BC BC, A C AC AC, A B AB AB 三边. (2) A 3 A_3 A3, B 3 B_3 B3, C 3 C_3 C3 三点共线.
(1) 先证明 P 1 A ⊥ B C P_{1}A\bot BC P1A⊥BC, 其余可同理证明.
过 P P P 和 A A A 作 B C BC BC 的垂线交 B C BC BC 于 A 0 A_{0} A0, A 0 ′ A_{0}' A0′.
可求得 C 2 A 0 / B 1 A 0 = tan C / 2 / tan B / 2 C_2 A_0/B_1 A_0=\tan C/2/\tan B/2 C2A0/B1A0=tanC/2/tanB/2.
C 2 A 0 ′ / B 1 A 0 ′ = O 3 A / O 2 A = O 3 C 2 / O 2 B 1 = C 2 C tan ( C / 2 ) / B 1 B / tan ( B / 2 ) = tan ( C / 2 ) / tan ( B / 2 ) C_2 A_{0}^{'}/B_1 A_{0}^{'}=O_{3}A/O_{2}A=O_{3}C_{2}/O_{2}B_{1}=C_{2}C \tan (C/2)/B_{1}B/\tan (B/2)=\tan (C/2)/\tan (B/2) C2A0′/B1A0′=O3A/O2A=O3C2/O2B1=C2Ctan(C/2)/B1B/tan(B/2)=tan(C/2)/tan(B/2)
(2) 设 A A 1 = B B 1 = C C 1 = x AA_1=BB_1=CC_1=x AA1=BB1=CC1=x
对 △ A B C \triangle ABC △ABC 和截线 P 1 P 2 P_1 P_2 P1P2 应用梅涅劳斯定理, A C 3 / B C 3 = A C 1 / C C 1 ⋅ C C 2 / B C 2 = ( x − b ) / ( x − a ) AC_3/ BC_3 = AC_{1}/CC_{1} \cdot CC_{2}/BC_{2}=(x-b)/(x-a) AC3/BC3=AC1/CC1⋅CC2/BC2=(x−b)/(x−a)
对 △ A B C \triangle ABC △ABC 和截线 P 2 P 3 P_2 P_3 P2P3 应用梅涅劳斯定理, B A 3 / C A 3 = A A 2 / C A 2 ⋅ B A 1 / A A 1 = ( x − c ) / ( x − b ) BA_3/ CA_3 = AA_{2}/CA_{2} \cdot BA_{1}/AA_{1}=(x-c)/(x-b) BA3/CA3=AA2/CA2⋅BA1/AA1=(x−c)/(x−b)
对 △ A B C \triangle ABC △ABC 和截线 P 1 P 3 P_1 P_3 P1P3 应用梅涅劳斯定理, C B 3 / A B 3 = B B 2 / A B 2 ⋅ C B 1 / B B 1 = ( x − a ) / ( x − c ) CB_{3}/AB_{3}=BB_{2}/AB_{2} \cdot CB_{1}/BB_{1}=(x-a)/(x-c) CB3/AB3=BB2/AB2⋅CB1/BB1=(x−a)/(x−c)
所以 A C 3 / B C 3 ⋅ B A 3 / C A 3 ⋅ C B 3 / A B 3 = 1 AC_3/ BC_3 \cdot BA_3/ CA_3 \cdot CB_{3}/AB_{3}=1 AC3/BC3⋅BA3/CA3⋅CB3/AB3=1. 由梅涅劳斯定理逆定理可知 P 1 , P 2 , P 3 P_{1}, P_{2}, P_{3} P1,P2,P3 三点共线.
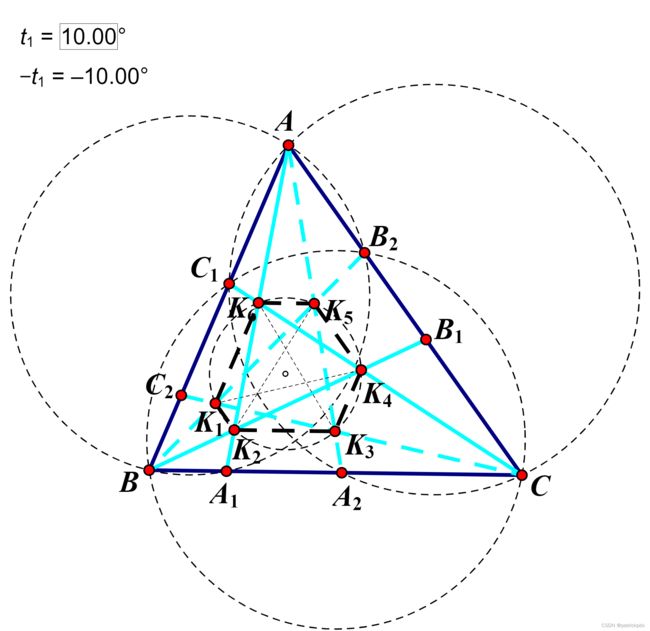
推论6. 如图, ∠ A A 1 A 2 = ∠ A A 2 A 1 = ∠ B B 1 B 2 = ∠ B B 2 B 1 = ∠ C C 1 C 2 = ∠ C C 2 C 1 \angle AA_1A_2= \angle AA_2A_1=\angle BB_1B_2= \angle BB_2B_1=\angle CC_1C_2= \angle CC_2C_1 ∠AA1A2=∠AA2A1=∠BB1B2=∠BB2B1=∠CC1C2=∠CC2C1, 求证: K 1 K_1 K1 ~ K 6 K_6 K6 共圆.
证明:
证明: 证明 K 5 K 6 / / B C K_{5}K_{6}// BC K5K6//BC:
显然 B B B, C C C, B 2 B_2 B2, C 1 C_1 C1 共圆; A A A, C C C, A 2 A_2 A2, C 1 C_1 C1 共圆; A A A, B B B, A 1 A_1 A1, B 2 B_2 B2 共圆
A K 6 / K 6 A 1 = A C 1 / B C 1 ⋅ B C / A 1 C AK_{6}/K_{6}A_{1}=AC_{1}/BC_{1}\cdot BC/A_{1}C AK6/K6A1=AC1/BC1⋅BC/A1C
A K 5 / K 5 A 2 = A B 2 / B 2 C ⋅ B C / B A 2 AK_{5}/K_{5}A_{2}=AB_{2}/B_{2}C\cdot BC/BA_{2} AK5/K5A2=AB2/B2C⋅BC/BA2
A B 2 / A C 1 = A B / A C AB_{2}/AC_{1}=AB/AC AB2/AC1=AB/AC, B C 1 / B A 2 = B C / A B BC_{1}/BA_{2}=BC/AB BC1/BA2=BC/AB, A B 2 / A C 1 = A B / A C AB_{2}/AC_{1}=AB/AC AB2/AC1=AB/AC, A 1 C / B 2 C = A C / B C A_{1}C/B_{2}C=AC/BC A1C/B2C=AC/BC
同理 K 2 K 3 / / B C K_{2}K_{3}//BC K2K3//BC, K 3 , K 6 , K 2 , K 5 K_{3}, K_{6}, K_{2}, K_{5} K3,K6,K2,K5 四点共圆, 同理还可得到 , K 1 , K 4 , K 3 , K 6 K_{1}, K_{4}, K_{3}, K_{6} K1,K4,K3,K6 四点共圆, K 1 , K 4 , K 2 , K 5 K_{1}, K_{4}, K_{2}, K_{5} K1,K4,K2,K5 四点共圆, 由戴维斯定理可知六点共圆.
推论7. 三个圆每两个的外公切线交点三点共线.
证明: 如图. 易证 O 1 O 2 O_{1}O_{2} O1O2 过 V 3 V_{3} V3, O 1 O 3 O_{1}O_{3} O1O3 过 V 2 V_{2} V2, O 2 O 3 O_{2}O_{3} O2O3 过 V 1 V_{1} V1. 对于 △ O 1 O 2 O 3 \triangle O_1 O_2 O_3 △O1O2O3 和 V 1 V_{1} V1, V 2 V_{2} V2, V 3 V_{3} V3, 易证
O 1 V 3 O 2 V 3 O 2 V 1 O 3 V 1 O 3 V 2 O 1 V 2 = r 1 r 2 r 2 r 3 r 3 r 1 = 1 \frac{O_{1}V_{3}}{O_{2}V_{3}} \frac{O_{2}V_{1}}{O_{3}V_{1}} \frac{O_{3}V_{2}}{O_{1}V_{2}} = \frac{r_1}{r_2}\frac{r_2}{r_3}\frac{r_3}{r_1} = 1 O2V3O1V3O3V1O2V1O1V2O3V2=r2r1r3r2r1r3=1
由梅涅劳斯定理逆定理可知, V 1 V_{1} V1, V 2 V_{2} V2, V 3 V_{3} V3 三点共线.
练习1. 如图, A B = A D AB=AD AB=AD, B C = C D BC=CD BC=CD, 过 B D BD BD 上的一点 P P P 作一条直线分别交 A D AD AD, B C BC BC 于 E E E, F F F, 再过点 P P P 作一条直线分别交 A B AB AB, C D CD CD 于 G G G, H H H. 设 G F GF GF 与 E H EH EH 分别交 B D BD BD 于 I I I, J J J, 求证: P I P B = P J P D \frac{PI}{PB}=\frac{PJ}{PD} PBPI=PDPJ.
正面: 过 B B B 作 A D AD AD, C D CD CD 的平行线, 分别交 G H GH GH, E F EF EF 于 L L L, M M M, 连结 L M LM LM. 易证 ∠ L B G = ∠ F B M \angle LBG=\angle FBM ∠LBG=∠FBM, ∠ G B P = ∠ M B P \angle GBP=\angle MBP ∠GBP=∠MBP. 所以
sin ∠ P B L sin ∠ G B L ⋅ sin ∠ G B I sin ∠ L B F ⋅ sin ∠ F B M sin ∠ P B M = 1 \frac{\sin\angle PBL}{\sin\angle GBL}\cdot \frac{\sin\angle GBI }{\sin\angle LBF}\cdot \frac{\sin\angle FBM}{\sin\angle PBM}=1 sin∠GBLsin∠PBL⋅sin∠LBFsin∠GBI⋅sin∠PBMsin∠FBM=1
由梅涅劳斯定理(第二角元形式)逆定理可知 L M LM LM 经过 I I I.
设 P I / P J = r PI/PJ=r PI/PJ=r, P E / P M = r PE/PM=r PE/PM=r, △ D E P ∼ △ B M P \triangle DEP\sim \triangle BMP △DEP∼△BMP, 所以 P D / P B = P E / P M = r PD/PB=PE/PM=r PD/PB=PE/PM=r.
练习2. 如图, △ A B C \triangle ABC △ABC 为非直角三角形, H H H 为垂心, D D D, E E E, F F F 为三角形三条垂线的垂足, 过 H H H 分别作三边的平行线, 三条线分别与 △ D E F \triangle DEF △DEF 三边所在直线相交, 求证三交点共线.
证明: 对于 △ F D E \triangle FDE △FDE, 截线 P Q R PQR PQR 和点 H H H, 易证
sin ∠ Q H F sin ∠ Q H D sin ∠ R H D sin ∠ R H E sin ∠ E H P sin ∠ F H P = cos A cos C cos B cos A cos C cos A = 1 \frac{\sin \angle QHF}{\sin \angle QHD} \frac{\sin \angle RHD}{\sin \angle RHE} \frac{\sin \angle EHP}{\sin \angle FHP} = \frac{\cos A}{\cos C}\frac{\cos B}{\cos A}\frac{\cos C}{\cos A} = 1 sin∠QHDsin∠QHFsin∠RHEsin∠RHDsin∠FHPsin∠EHP=cosCcosAcosAcosBcosAcosC=1
由梅涅劳斯定理第二角元形式的逆定理可知命题成立.
练习3. 如图, P P P 为 △ A B C \triangle ABC △ABC 外一点, 过 P P P 作 P A PA PA, P B PB PB, P C PC PC 的垂线分别交 B C BC BC, A C AC AC, A B AB AB 三边于点 D D D, E E E, F F F, 则 D D D, E E E, F F F 三点共线.
由第二角元形式易证
练习4. 如图, 已知 A C AC AC 平分 ∠ B A D \angle BAD ∠BAD, 求证 ∠ G A C = ∠ F A C \angle GAC = \angle FAC ∠GAC=∠FAC.
对 △ D F C \triangle DFC △DFC 和截线 E P B EPB EPB 应用梅涅劳斯定理, 可知
sin F A C / sin E A C = sin F A B / sin E A D \sin FAC / \sin EAC = \sin FAB/\sin EAD sinFAC/sinEAC=sinFAB/sinEAD
若 ∠ F A C > ∠ E A C \angle FAC>\angle EAC ∠FAC>∠EAC, 则 ∠ F A B > ∠ E A D \angle FAB>\angle EAD ∠FAB>∠EAD, 进而 ∠ B A C > ∠ C A D \angle BAC>\angle CAD ∠BAC>∠CAD.
练习5. 如图, A 1 A_{1} A1 为 B C BC BC 中点, A 2 A_{2} A2 为 ∠ B A C \angle BAC ∠BAC 角平分线与 B C BC BC 的交点, K A 2 / / A C KA_{2}//AC KA2//AC, 求证: A A 2 ⊥ K C AA_{2}\bot KC AA2⊥KC.
作 C K CK CK 的垂线交 B C BC BC 于 A 2 ′ A_{2}' A2′, 对 △ B D C \triangle BDC △BDC 和截线 A E A 2 AEA_{2} AEA2 应用梅涅劳斯定理可知
D A ⋅ B A 2 ′ ⋅ C E A B ⋅ A 2 ′ C ⋅ D E = 1 \frac{DA \cdot BA_{2}' \cdot CE}{AB \cdot A_{2}'C \cdot DE} =1 AB⋅A2′C⋅DEDA⋅BA2′⋅CE=1
B A 2 ′ A 2 ′ C = A B A C \frac{BA_{2}'}{A_{2}'C}=\frac{AB}{AC} A2′CBA2′=ACAB, 所以 A 2 ′ A_{2}' A2′ 就是 A 2 A_{2} A2
练习x. 如图, G G G 为 △ A B C \triangle ABC △ABC 的垂心, X Y XY XY 为过 G G G 平行于 B C BC BC 的直线, M M M 为 B C BC BC 中点, 求证 △ Q P M ∼ △ A B C \triangle QPM \sim \triangle ABC △QPM∼△ABC.
练习6.
如图, D D D, E E E 为以 B C BC BC 为直径所作的圆分别与 A B AB AB, A C AC AC 的交点, D F ⊥ B C DF \bot BC DF⊥BC, E G ⊥ B C EG \bot BC EG⊥BC, 求证: P M PM PM 在过 A A A 向 B C BC BC 所作的垂线上.
显然 P P P 是垂心, 设 A P AP AP 的垂足为 Q Q Q, A P AP AP 交 E F EF EF 于 M ′ M' M′, 交 D G DG DG 于 M ′ ′ M'' M′′
对 △ E F C \triangle EFC △EFC 和截线 A Q AQ AQ 应用梅涅劳斯定理, 可知
F M ′ / M ′ E = F Q / Q C ⋅ C A / A E FM'/M'E=FQ/QC \cdot CA/AE FM′/M′E=FQ/QC⋅CA/AE,
同理
D M ′ ′ / M ′ ′ G = A D / A B ⋅ B Q / Q G DM''/M''G=AD/AB \cdot BQ/QG DM′′/M′′G=AD/AB⋅BQ/QG
F Q / Q C ⋅ C A / A E A D / A B ⋅ B Q / Q G = ( A B ⋅ A C ) ⋅ F Q ⋅ G Q ( A D ⋅ A E ) ⋅ B Q ⋅ C Q = 1 \frac{FQ/QC \cdot CA/AE}{AD/AB \cdot BQ/QG}=\frac{(AB\cdot AC) \cdot FQ \cdot GQ}{(AD\cdot AE) \cdot BQ \cdot CQ}=1 AD/AB⋅BQ/QGFQ/QC⋅CA/AE=(AD⋅AE)⋅BQ⋅CQ(AB⋅AC)⋅FQ⋅GQ=1
( F Q / B Q = A D / A B FQ/BQ=AD/AB FQ/BQ=AD/AB, G Q / C Q = A E / A C GQ/CQ=AE/AC GQ/CQ=AE/AC)
所以 M ′ M' M′ 与 M ′ ′ M'' M′′ 重合, 说明 M ′ M' M′ 也在 D G DG DG 上, 因此就是 M M M.
练习7. 如图, A B C D ABCD ABCD 为平行四边形, M N / / A B MN//AB MN//AB, E F / / A B EF//AB EF//AB, 求证: M F MF MF, B D BD BD, E N EN EN 三线共点.
证明: 设 M F MF MF 交 B D BD BD 于 G G G, E N EN EN 交 B D BD BD 于 G ′ G' G′, 对于 △ A B D \triangle ABD △ABD 和截线 F M G FMG FMG, △ C B D \triangle CBD △CBD 和截线 E N G ′ ENG' ENG′ 分别应用梅涅劳斯定理, 可以证得 B G / D G = B G ′ / D G ′ BG/DG=BG'/DG' BG/DG=BG′/DG′, 因此 G G G 和 G ′ G' G′ 重合.
练习8. 如图, P P P 为 △ A B C \triangle ABC △ABC 内一点, P A PA PA, P B PB PB, P C PC PC 的垂线分别交 B C BC BC, A C AC AC, A B AB AB 三边所在直线于 A ′ , B ′ , C ′ A', B', C' A′,B′,C′, 求证这三点共线.
证明: 对 △ A B C \triangle ABC △ABC 和 A ′ , B ′ , C ′ A', B', C' A′,B′,C′, 以及点 P P P, 易证
sin ∠ B ′ P A sin ∠ B ′ P C sin ∠ C P A ′ sin ∠ B P A ′ sin ∠ B P C ′ sin ∠ A P C ′ = 1 \frac{\sin \angle B'PA}{\sin \angle B'PC} \frac{\sin \angle CPA'}{\sin \angle BPA'} \frac{\sin \angle BPC'}{\sin \angle APC'} = 1 sin∠B′PCsin∠B′PAsin∠BPA′sin∠CPA′sin∠APC′sin∠BPC′=1
由梅涅劳斯定理第二角元形式逆定理可整得此结论.
塞瓦定理可用面积法证明, 具体略.