数据结构：二叉树（先、中、后序）

一、实现功能描述：

1、使用先序序列来创建二叉树，并使用递归算法实现先序、中序、后序输出。
2、使用先序序列来创建二叉树，并使用非递归算法实现先序、中序、后序输出。
3、使用中序、后序的序列来创建二叉树，并使用先序输出。
4、层序遍历的递归与非递归算法
5、实现另外一种后序非递归遍历的算法

二、方案比较与选择

1、从数据结构的逻辑结构与存储结构角度提供多种解决方案；
存储结构：
①二叉树的顺序存储，寻找后代节点和祖先节点都非常方便，但对于普通的二叉树，顺序存储浪费大量的存储空间，同样也不利于节点的插入和删除。因此顺序存储一般用于存储完全二叉树。
②链式存储相对顺序存储节省存储空间，插入删除节点时只需修改指针，但寻找指定节点时很不方便。不过普通的二叉树一般是用链式存储结构。

逻辑结构：
二叉树不等同于树，是另一种树结构。
二叉树的优势：
有序数组的优势在于二分查找，链表的优势在于数据项的插入和数据项的删除。但是在有序数组中插入数据就会很慢，同样在链表中查找数据项效率就很低。综合以上情况，二叉树可以利用链表和有序数组的优势，同时可以合并有序数组和链表的优势。
二叉树还可分为满二叉树、一般二叉树、完全二叉树。

2、从时空效率角度分析决定最终采用方案的原因。
链式存储相对顺序存储可节省存储空间，插入删除节点时只需修改指针，而且无论使用顺序、链式进行存储，遍历对n个结点的二叉树时间复杂度均为O(n)。且链表的优势在于数据项的插入和数据项的删除。

三、设计算法描述

1、用简单示例结合所设计算法采用的数据逻辑结构图、存储结构图说明算法思想。
二叉树的逻辑结构：

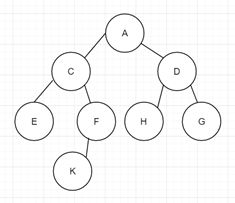
二叉树的存储结构：

先序遍历：（数字表示遍历输出顺序）

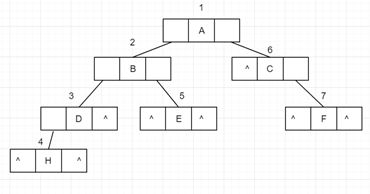
中序遍历：（数字表示遍历输出顺序）

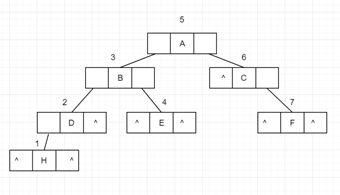
后序遍历：（数字表示遍历输出顺序）

2、进行模块划分，给出功能组成框图。形式如下：
非递归算法：

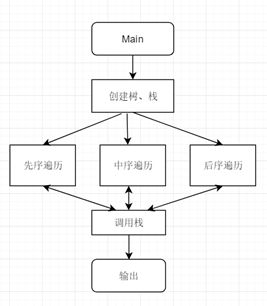
递归算法：

四、算法实现（即完整源程序，带注解）

先序创建树的递归遍历：

#include 
#include 
#define MAXSIZE 100
#define FALSE 0
typedef char ElemType;

typedef struct BiTreeNode
{
	ElemType data; //存放数据
	struct BiTreeNode *lchild;  //左孩子
	struct BiTreeNode *rchild; //右孩子
}BiTreeNode, *BiTree;


void menu()                     //打印菜单，供用户选择要执行的功能。
{
	printf("\n");
	printf("**************************\n");
	printf("*******1.按先序遍历*******\n");
	printf("*******2.按中序遍历*******\n");
	printf("*******3.按后序遍历*******\n");
	printf("*******0. 推出程序 *******\n");
	printf("**************************\n");
	printf("\n");
}
void CreateBiTree(BiTree *T)             //使用先序的方式创建二叉树
{
	char tree;                           //定义的tree变量用来接收创建二叉树时输入的字符
	scanf_s("%c", &tree);
	if (tree == '#')
		*T = NULL;
	else
	{
		*T = (BiTree)malloc(sizeof(BiTreeNode));  //使用链式进行存储
		(*T)->data = tree;
		CreateBiTree(&(*T)->lchild);
		CreateBiTree(&(*T)->rchild);
	}
}
void PreOrderTravel(BiTree T)                //先序遍历二叉树
{
	if (T == NULL)
		return;
	printf("%c ", T->data);
	PreOrderTravel(T->lchild);
	PreOrderTravel(T->rchild);
}
void InOrderTravel(BiTree T)                //中序遍历二叉树
{
	if (T == NULL)
		return;
	InOrderTravel(T->lchild);
	printf("%c ", T->data);
	InOrderTravel(T->rchild);
}
void TailOrderTravel(BiTree T)          //后序遍历二叉树 
{
	if (T == NULL)
		return;
	TailOrderTravel(T->lchild);
	TailOrderTravel(T->rchild);
	printf("%c ", T->data);
}
int main()
{
	int input;
	BiTree T;
	printf("创建二叉树\n");
	printf("请给二叉树按照先序方式依次输入结点的值(空结点为#):\n");
	CreateBiTree(&T);
	do
	{
		menu();
		printf("please enter your choice:");
		scanf_s("%d", &input);
		switch (input)
		{
		case 1: printf("先序方式遍历结果：");
			PreOrderTravel(T);
			printf("\n");
			break;
		case 2:printf("中序方式遍历结果：");
			InOrderTravel(T);
			printf("\n");
			break;
		case 3:printf("后序方式遍历结果：");
			TailOrderTravel(T);
			printf("\n");
			break;
		case 0:
			printf("退出程序\n");
			break;
		default:
			printf("输入错误！请重新输入。\n");
		}
	} while (input);
	return 0;
}

先序创建树的非递归遍历：

#include 
#include 
#define M 100 
typedef char ElemType;

typedef struct node
{
	ElemType data;
	ElemType num;
	struct node *lchild;
	struct node *rchild;  //树节点中num是为了计数用。在后序遍历中，子树的根节点在第一次遍历的时候不会输出，只有在第二次遍历的时候才输出。
}bitree;


typedef struct stack
{
	bitree *elements[M];
	int top;
}seqstack;//定义一个储存树类型地址的栈，方便遍历的时候追踪到树的地址。

bitree *root;//定义一个树根
seqstack s;//定义栈

void setnull()//初始化栈
{
	s.top = 0;
}

void push(bitree *temp)//入栈操作
{
	s.elements[s.top++] = temp;
}

bitree *pop()//取栈顶并出栈顶
{
	return s.elements[--s.top];
}

int empty()//判断空栈
{
	return s.top == 0;
}

void menu()                     //打印菜单，供用户选择要执行的功能。
{
	printf("\n");
	printf("**************************\n");
	printf("*******1.按先序遍历*******\n");
	printf("*******2.按中序遍历*******\n");
	printf("*******3.按后序遍历*******\n");
	printf("*******0. 推出程序 *******\n");
	printf("**************************\n");
	printf("\n");
}

bitree *creat()   /*建立二叉树的递归算法*/
{
	bitree *t;
	ElemType x;
	scanf_s("%c", &x);
	if (x == '#')
		t = NULL; /*以x=0表示输入结束*/
	else {
		t = (bitree*)malloc(sizeof(bitree));//动态生成结点t,分别给结点t的数据域、左右孩子域  
		t->data = x;                  //赋值,给左右孩子域赋值时用到了递归的思想。
		t->lchild = creat();
		t->rchild = creat();
	}
	return t;
}

void preorder(bitree *t)//前序遍历的非递归算法
{
	bitree *temp = t;//定义一个树节点，用它来遍历
	while (temp != NULL || s.top != 0)
	{
		while (temp != NULL)//先遍历左孩子，并输出。
		{
			printf("%4c", temp->data);
			push(temp);
			temp = temp->lchild;
		}
		if (s.top != 0)//当左孩子遍历完后，取栈顶，找右孩子。此时循环还没有结束，再遍历它的左孩子，直至孩子全部遍历结束。
		{
			temp = pop();
			temp = temp->rchild;
		}
	}
	printf("\n");
}

void inorder(bitree *t)//中序遍历的非递归算法
{
	bitree *temp = t;
	while (temp != NULL || s.top != 0)
	{
		while (temp != NULL)//先把左孩子入栈，所有左孩子入栈结束
		{
			push(temp);
			temp = temp->lchild;
		}
		if (s.top != 0)//左孩子入栈结束，取栈顶，输出栈顶元素，遍历右孩子
		{
			temp = pop();
			printf("%4c", temp->data);
			temp = temp->rchild;
		}
	}
	printf("\n");
}


void laorder(bitree *root)//后序遍历的非递归算法
{
	bitree *temp = root;
	while (temp != NULL || s.top != 0)
	{
		while (temp != NULL)
		{
			temp->num = 1;       // 当前节点首次被访问
			push(temp);
			temp = temp->lchild;
		}
		if (s.top != 0)
		{
			temp = pop();
			if (temp->num == 1)   // 第一次出现在栈顶
			{

				temp->num++;
				push(temp);
				temp = temp->rchild;
			}
			else
				if (temp->num == 2)//第二次输出并制空，防止陷入死循环
				{
					printf("%4c", temp->data);
					temp = NULL;
				}
		}
	}
	printf("\n");
}


int main()
{
	int input;
	bitree *root;//创建根
	setnull();//制空栈
	printf("请按先序输入二叉树的结点：\n");
	root = creat();//创建二叉树:尝试输入:ABC##D##EF##G##

	menu();
	printf("请输入选择的遍历的方式：\n");
	scanf_s("%d", &input);
	do
	{
		menu();
		printf("please enter your choice:");
		scanf_s("%d", &input);
		switch (input)
		{
		case 1: printf("先序方式遍历结果：");
			preorder(root);
			printf("\n");
			break;
		case 2:printf("中序方式遍历结果：");
			inorder(root);
			printf("\n");
			break;
		case 3:printf("后序方式遍历结果：");
			laorder(root);
			printf("\n");
			break;
		case 0:
			printf("退出程序\n");
			break;
		default:
			printf("输入错误！请重新输入。\n");
		}
	} while (input);
	return 0;
}

先序创建树的递归层序遍历：

#include 
#include 
#define M 100 
typedef char ElemType;

typedef struct node
{
	ElemType data;
	ElemType num;
	struct node *lchild;
	struct node *rchild;  //树节点中num是为了计数用。在后序遍历中，子树的根节点在第一次遍历的时候不会输出，只有在第二次遍历的时候才输出。
}bitree;

int bitreedepth(bitree* t)//二叉树的深度
{
	int dep1, dep2;
	if (!t)return 0;
	else
	{
		dep1 = bitreedepth(t->lchild);
		dep2 = bitreedepth(t->rchild);
	}
	return (dep1 > dep2 ? dep1 + 1 : dep2 + 1);
}
int levelordertraverse1(bitree* t, int i)//二叉树层序的递归
{
	if (!t || i == 0) return 1;
	if (i == 1)
	{
		printf("%c ", t->data);
		return 0;
	}
	levelordertraverse1(t->lchild, i - 1);
	levelordertraverse1(t->rchild, i - 1);
	return 0;
}
int levelordertraverse2(bitree* t)//二叉树层序遍历，递归
{
	if (!t)return 1;
	int dep = bitreedepth(t);
	for (int i = 1; i <= dep; ++i) levelordertraverse1(t, i);
	return 0;
}


bitree *creat()   /*建立二叉树的递归算法*/
{
	bitree *t;
	ElemType x;
	scanf_s("%c", &x);
	if (x == '#')
		t = NULL; /*以x=0表示输入结束*/
	else {
		t = (bitree*)malloc(sizeof(bitree));//动态生成结点t,分别给结点t的数据域、左右孩子域  
		t->data = x;                  //赋值,给左右孩子域赋值时用到了递归的思想。
		t->lchild = creat();
		t->rchild = creat();
	}
	return t;
}

int main()
{
	bitree *root;//创建根
	printf("请按先序输入二叉树的结点：\n");
	root = creat();//创建二叉树:尝试输入:ABC##D##EF##G##

	levelordertraverse2(root);
	return 0;
}

先序创建树的非递归层序遍历：

#include 
#include 
#include 

#define MaxSize 100
typedef char ElemType;

typedef struct node
{
	ElemType data;
	struct node* lchild;
	struct node* rchild;
}bitree;

typedef struct queue
{
	struct node* numQ[MaxSize];
	int front;
	int rear;
}Queue;

Queue Q;

void initilize()  //初始化队列
{
	Q.front = 0;
	Q.rear = 0;
}

void Push(bitree* root) //入队
{ 
	Q.numQ[++Q.rear] = root;
}

bitree* Pop() //出队
{ 
	return Q.numQ[++Q.front];
}

int empty() //判断对列是否为空
{ 
	return Q.rear == Q.front;
}

bitree* creatTree(bitree* root)   /*建立二叉树的递归算法*/
{
	char x;
	scanf_s("%c", &x);
	if (x == '#')
		root = NULL; /*以x=0表示输入结束*/
	else {
		root = (bitree*)malloc(sizeof(bitree));//动态生成结点t,分别给结点t的数据域、左右孩子域  
		root->data = x;                  //赋值,给左右孩子域赋值时用到了递归的思想。
		root->lchild = creatTree(root->lchild);
		root->rchild = creatTree(root->lchild);
	}
	return root;
}



void LevelOrderTraversal(bitree* root) //二叉树的层次遍历
{ 
	bitree* temp;
	Push(root);
	while (!empty()) {
		temp = Pop();
		printf("%c ", temp->data);  //输出队首结点
		if (temp->lchild)     //把Pop掉的结点的左子结点加入队列
			Push(temp->lchild);
		if (temp->rchild)    把Pop掉的结点的右子结点加入队列
			Push(temp->rchild);
	}
}

int main() 
{
	printf("请按照先序输入节点：");
	bitree* root = NULL;
	root = creatTree(root);
	initilize();  //初始化队列
	printf("层序遍历输出：\n");
	LevelOrderTraversal(root);
	putchar('\n');

	return 0;
}

另外一种后序非递归遍历的算法：

void pastOrder_NR(Bitree root)
{
	if (NULL == root)
		cout << "empty" << endl;

	Bitree cur = root;
	Bitree last = NULL;
	stack<Bitree> s;

	while (cur || !s.empty())
	{
		while (cur)//压入左子树结点
		{
			s.push(cur);
			cur = cur->_left;
		}

		cur = s.top();

		if (cur->_right && last != cur->_right)//考虑栈顶结点的右子树结点。存在且没被访问过，将右子树结点压入栈中
		{
			cur = cur->_right;
		}
		else if ((NULL == cur->_right) || (last == cur->_right))
			//右子树结点为空或者已经被访问过，则访问栈顶结点并弹出
		{
			cout << cur->_data << "->";
			last = cur;//更新last值
			s.pop();
			//cur置空作用在于当原栈顶结点被访问并弹出后，下一层while是将当前栈顶结点的左子树入栈，当前栈顶结点的左子树已经被遍历过，		
			//因此会造成死循环，所以将cur置空，直接考虑当前栈顶结点的右子树            
			//一旦某个结点入栈，首先会遍历这个结点的左子树，然后考虑右子树的情况
			cur = NULL;
		}
	}cout << "over" << endl;
}

使用中序和后序创建二叉树：

void rebuild(int *inlist, int *postlist, int n, bitree **t)
{
	if (!inlist || !postlist || n <= 0)		//空树 
		return;
	int i;

	//找到根结点在中序遍历中的位置 
	for (i = 0; i < n; i++)
	{
		if (inlist[i] == postlist[n - 1])
			break;
	}

	if (i >= n)
		return;

	//初始化根结点 
	*t = (bitree*)malloc(sizeof(bitree));
	if (!t)
		return;
	(*t)->lchild = (*t)->rchild = NULL;
	(*t)->data = postlist[n - 1];


	//重建左子树	
	rebuild(inlist, postlist, i, &(*t)->lchild);
	//重建右子树 
	rebuild(inlist + i + 1, postlist + i, n - i - 1, &(*t)->rchild);	//post+i 
}

五、实验结果测试与分析

1、用各种可能数据测试程序，取截图；
先序创建二叉树（递归遍历）：【输入空节点用#代替】

先序创建二叉树（非递归遍历）：【输入空节点用#代替】


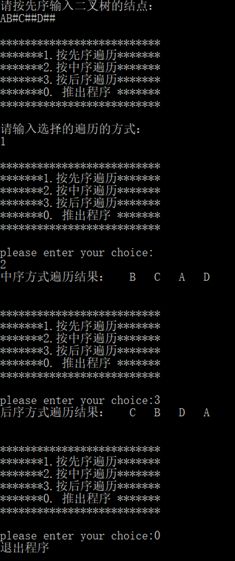
先序创建二叉树（非递归层序遍历）：【输入空节点用#代替】

先序创建二叉树（递归层序遍历）: 【输入空节点用#代替】

六、分析

后序遍历递归定义：先左子树，后右子树，再根节点。

后序遍历的难点在于：需要判断上次访问的节点是位于左子树，还是右子树。若是位于左子树，则需跳过根节点，先进入右子树，再回头访问根节点；若是位于右子树，则直接访问根节点。

后序遍历的非递归，基本使用栈和标志点来实现；分别有使用两个栈、一个栈和两个标志点、一个栈和一个标志点。其时空复杂度均相同。