数据结构-C语言实现堆（超长超详细）

一、定义

1、理论定义

堆(Heap)是计算机科学中一类特殊的数据结构，是最高效 的优先级队列。堆通常是一个可以被看做一棵完全二叉树的数组对象。

2、结构

1）逻辑结构

逻辑结构是便于人理解而形成的一种结构。
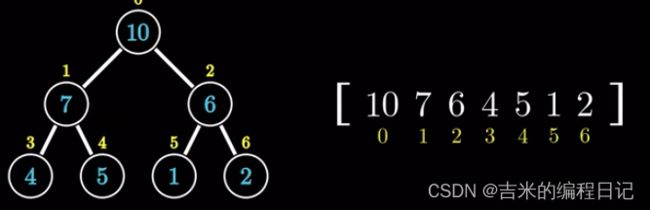
上文提到，堆可以被看成一棵完全二叉树，那么堆的逻辑结构就可以用二叉树来表示。

2）物理结构

物理结构是计算机存储数据时应用的一种结构。
堆的重要功能是存储数据，所以堆实际上是用一维数组存储数据，堆的物理结构就是一维数组。

二、堆序性

1、大堆（小堆）

所有的父节点都大于等于子节点。
所有的父节点都小于等于子节点。

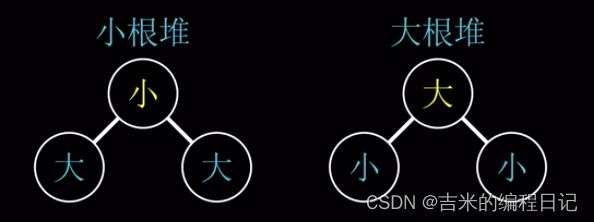
举个例子

三、基本操作

1、向上调整

作用

这种操作主要用于在堆尾部插入一个数据。
这里我以把现有的堆调成大堆为例。
操作流程：破坏了堆序性的节点和他的父节点比较，如果他比父节点大，则交换他们，循环这样的操作，直到该节点来到堆的顶或者满足大堆才停止循环。

代码实现

void AdjustUp(HPDataType* a, int child)
 9	{
 10		int parent = (child - 1) / 2;
 11		while (child > 0)
 12		{
 13			
 14			if (a[child] < a[parent])
 15			{		
 16				//交换
 17				Swap(&a[child], &a[parent]);
 18				//迭代，更新child和parent
 19				child = parent;
 20				parent = (parent - 1) / 2;
 21			}
 22			else
 23			{
 24				break;
 25			}
 26		
 27		}
 28	}
 29	

2、向下调整

作用

这种操作主要用于在堆顶部插入一个数据。
这里我以把现有的堆调成大堆为例。
操作流程：根节点和他的孩子节点中较大的比较（这里我后文直接说成和大孩子比较噢），如果根节点比大孩子小，则交换他们，循环这样的操作，直到根节点来到堆的底或者满足大堆才停止循环。

代码实现

//size是数组的元素个数，root是根节点
 31	void AdjustDown(HPDataType* a, int size, int root)
 32	{
 33		size_t parent = root;
 34		size_t child = parent * 2 + 1;
 35		while (child < size)
 36		{
 37			// 1、选出左右孩子中大的那个
 38			if (child + 1 < size && a[child + 1] >a[child])
 39			{
 40				++child;
 41			}
 42	
 43			// 2、如果孩子大于父亲，则交换，并继续往下调整
 44			if (a[child] > a[parent])
 45			{
 46				Swap(&a[child], &a[parent]);
 47				parent = child;
 48				child = parent * 2 + 1;
 49			}
 50			else
 51			{
 52				break;
 53			}
 54		}
 55	
 56	}
 57	

四、建堆

1、自上而下

操作流程：插入一个数–>向上调整

2、自下而上

操作流程：先建好一个堆，在底部插入一个数–>从该节点的父节点向下调整。

3、插入一个数

假设要在堆底插入一个数

操作流程

插入一个新节点–>数组size+1–>向上调整（保持原来的堆序性）

代码实现

//插入一个数
 97	//在堆底插入一个数
 98	void HPPush(HP* php, HPDataType x)
 99	{
 100		assert(php);
 101		if (php->capacity == php->size)
 102		{
 103			int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
 104			HPDataType* tmp = realloc(php->a,sizeof(HPDataType) * newcapacity);
 105			if (tmp == NULL)
 106			{
 107				printf("error");
 108				exit(-1);
 109			}
 110			php->a = tmp;
 111			php->capacity = newcapacity;
 112			
 113		}
 114		php->a[php->size ] = x;
 115		php->size++;
 116		//向上调整
 117		AdjustUp(php->a, php->size-1);
 118	
 119	}

4、删除一个数

假设要删除堆底的一个数

操作流程

交换堆底节点和根节点–>数组size-1–>向下调整（保持原来的堆序性）

代码实现

//删除一个数
 121	void HPPop(HP* php)
 122	{
 123		assert(php);
 124		assert(php->size > 0);
 125		Swap(&php->a[0],& php->a[php->size - 1]);
 126		php->size--;
 127		AdjustDown(php->a, php->size, 0);
 128	}
 129	

五、其他操作

1、初始化函数

//初始化函数
 66	void HPInit(HP* php)
 67	{
 68		assert(php);
 69		php->a = NULL;
 70		php->capacity = php->size = 0;
 71	}

2、打印函数

//打印函数
 73	void HPPrint(HP* php)
 74	{
 75		int i = 0;
 76		for (i = 0; i < php->size; i++)
 77		{
 78			printf("%d ", php->a[i]);
 79		}
 80		printf("\n");
 81	}

3、交换函数

这里注意：
⚠️要改变传过来的两个数，要传指针。

//交换函数
 59	void Swap(HPDataType* pa, HPDataType* pb)
 60	{
 61		HPDataType tmp = *pa;
 62		*pa = *pb;
 63		*pb = tmp;
 64	}

4、取出堆顶元素

//得到堆顶元素
 139	HPDataType HPTop(HP* php)
 140	{
 141		assert(php);
 142		assert(php->size > 0);
 143		return php->a[0];
 144	
 145	}

5、判断是否为空

bool类型返回【0】或【1】
⚠️这里返回的是表达式，中间用==链接。

bool HPEmpty(HP* php)
 84	{
 85		return php->size == 0;
 86	}

6、得到堆节点个数

//得到堆元素个数
 132	size_t HPSize(HP* php)
 133	{
 134		assert(php);
 135		return php->size;
 136	}
 137	

7、释放空间

//销毁空间
 88	void HPDestroy(HP* php)
 89	{
 90		assert(php);
 91		free(php->a);
 92		php->a = NULL;
 93		php->capacity = php->size = 0;
 94	}
 95