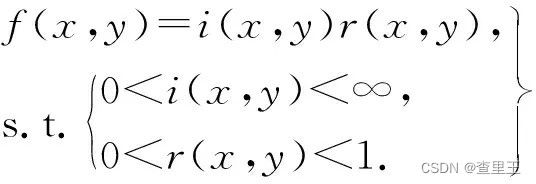图像翻拍检测——反射分量分离的特征融合
随着计算机技术的迅速发展,需要建立人与信息一一对应的安保认证技术,通过建立完整的映射网络体系,从而确保每个人的人身、财产、隐私等的安全.与指纹、基因等人体生物特征识别系统相比,人脸识别系统更加友好,不需要人的参与配合,能在不打扰正常生活情况下解决问题.同时,通过分析人脸识别系统的表情、姿态等可获得更多的有用信息.因此,人脸识别技术可用于公安系统、驾驶核对系统、监控系统、银行信用卡验证系统等[1].
随着深度神经网络的发展,深度神经网络在人脸识别中的应用日渐增多[2-5],识别准确率超过人类平均水平.当前,人脸识别主要针对二维图像或二维视频序列[6-7],而影响人脸识别的光照、姿态、年龄、遮挡等问题并没有得到根本解决[8].因此,不少不法分子使用翻拍图像伪装自我身份,以此欺骗人脸身份认证软件,并侵害他人利益.
目前,不少学者对翻拍图像的识别进行研究.孙锟[9]提供一种基于局部二值模式(LBP)水印特征和细粒度识别的图像防伪方法.Chen等[10]基于翻拍图像与真实图像虹膜的差别,对图像进行翻拍检测.文献[11]方法是基于同态滤波的自适应补偿图像光照加强的特征,将图像16等分,提取每一等分的八方向梯度比例特征,以此进行翻拍图像检测,该方法在训练集、测试集中人数较少,且翻拍人脸与真实人脸为同一人时的效果较好;
但当训练集、测试集中人数较多时,且翻拍人脸与真实人脸为不同人时准确率快速下降.文献[12]方法是建立翻拍图像与活体拍摄图像之间的梯度差异模型,并通过该模型提取三色(RGB)同道梯度特征进行分类.以上两种方法在活体数量较少、翻拍图像与活体拍摄图像均属于同一批活体时的效果较好,但当活体数量增加、翻拍图像与活体拍摄图像所属群体不同时,其准确率有一定程度下降.钱芸等[13]在液晶显示器介质下,基于纹理、细节缺失等特征对图像进行翻拍.本文对反射分量分离的特征融合图像翻拍检测进行研究.
1.1 图像形成模型
若用f(x,y)表示图像,则f(x,y)可用入射分量(入射到被观察场景的光源照射总量)、反射分量(场景中物体所反射的光照总量)两个分量表示[14].入射分量、反射分量分别记为i(x,y)与r(x,y),则f(x,y)为
(2) 通过构造线性算子H进行映射,使反射分量与入射分量进行不同的变换,即
H(x,y)[lnf(x,y)]=H(x,y)[lni(x,y)]+H(x,y)[lnr(x,y)].(3) 经典的同态滤波往往用于增强高频反射贡献、衰减低频照射贡献,从而达到增强图像细节信息的目的,其构造的高通滤波器形式为
(4) 式(4)中:γH,γL分别为高频分量及低频分量滤波的系数.
为使滤波器能够将反射分量分离,将低频分量系数γL设置为0,高频分量γH设置为1(约束条件来源于对图像频率图的拟合[15]),即
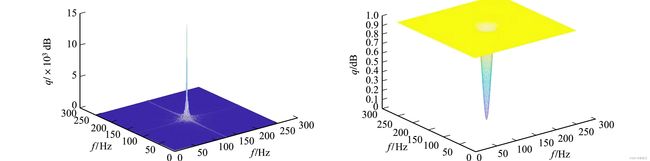
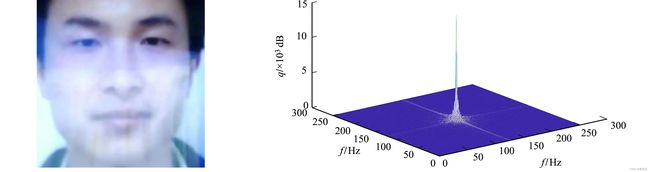
(5) 频谱图,如图1所示.图1中:q为强度;
f为频率.滤波器图,如图2所示.由图1,2可知:滤波器对位于频谱图中心的低频分量产生了抑制作用,而对高频分量保持不变.由此,式(3)近似变换为
图1 频谱图 图2 滤波器图Fig.1 Frequency spectrum diagram Fig. 2 Filter diagram
(6) 进一步可近似为
H(x,y)[lnf(x,y)]=[lnr(x,y)].(7) 对式(7)进行变换,有
fr(x,y)=e=e.(8) 化简得到
fr(x,y)=r(x,y).1.3 在翻拍图像上的应用
翻拍图像与活体拍摄图像主要差别在亮度通道的信息,因此,将原RBG三通道图像转化为HSV(hue, saturation, value)图像后提取亮度通道,对其进行对数变换,傅里叶变换后进行中心化.将低频部分转化至中心位置,高频部分转化至频谱图边缘位置.首先,将中心化后的频谱图乘以改造后的滤波器;
其次,对高、低频分量进行映射,对结果去中心化后进行傅里叶反变换;
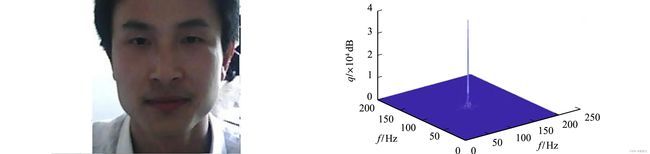
最后,指数变换后转化为原图像.原图,如图3所示.原图的傅里叶频谱图,如图4所示.
图3 原图 图4 原图的傅里叶频谱图 Fig.3 Original diagram Fig.4 Fourier frequency spectrum diagram of original diagram
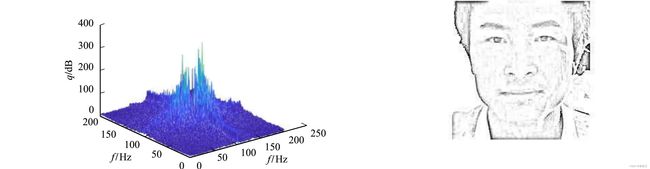
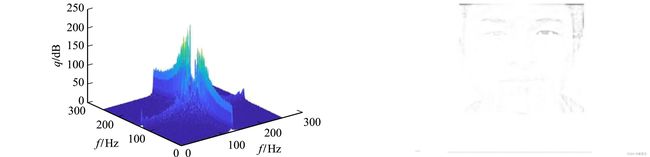
原图滤波器变换后的频谱图,如图5所示.原图亮度通道的最终图像,如图6所示.
图5 原图滤波器变换后的频谱图 图6 原图亮度通道的最终图像 Fig.5 Frequency spectrum diagram after filter Fig.6 Final diagram of brightness transformation of original diagram channel of original diagram
翻拍图像,如图7所示.翻拍图像的傅里叶频谱图,如图8所示.翻拍图像滤波器变换后的频谱图,如图9所示.翻拍图像亮度通道的最终图像,如图10所示.
图7 翻拍图像 图8 翻拍图像的傅里叶频谱图 Fig.7 Recapture diagram Fig.8 Fourier frequency spectrum diagram of recapture diagram
图9 翻拍图像滤波器变换后的频谱图 图10 翻拍图像亮度通道的最终图像 Fig.9 Frequency spectrum diagram after filter Fig.10 Brightness channel final transformation of recapture diagram diagram of recapture diagram
由图3~10可知:
翻拍图像与活体拍摄图像存在视觉上的差别,即图像下半部分为非正常反光,介质较均匀的反射图像削弱了漫反射分离,使原图的纹理特征模糊;
亮度通道强化了由于介质不同而产生的视觉差别.
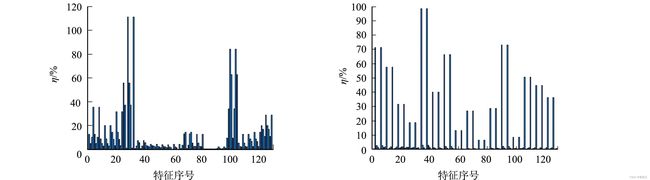
将亮度通道最终图像分别按行列做4等分划分,整幅图像划分为16等分,用Sobel算子将划分结果在八方向中进行计算[1].图像划分,如图11所示.特征提取,如图12所示.图12中:η为准确率.
(a) 1号方向掩模 (b) 2号方向掩模 (c) 3号方向掩模 (d) 4号方向掩模 (e) 5号方向掩模
(a) 活体拍摄图像 (b)翻拍图像 图12 特征提取Fig.12 Feature extraction
文中方法对文献[11]方法进行改动,计算每个区域各方向梯度值之和占整幅图像八方向梯度值对应总和的比例,将128(16×8)个特征通过支持向量机(SVM)进行分类,使用高斯核,对BoxConstraint,KernelScale两参数进行优化,模糊的纹理特征反映了直方图聚集性被削弱,变得更为均匀.
1.4 实验结果
将多个电信营业厅的摄像头采集的真实信息作为正样本,在各种复杂、恶劣环境下翻拍液晶显示屏,以电信营业厅摄像头翻拍的实体照片、各类证件照片作为负样本.样本模拟现实的复杂环境,具有较高的价值,共获取翻拍图像14 743张,活体拍摄图像14 121张.随机抽取翻拍图像、活体图像各200张进行实验,其中,活体图像中包含的活体数目为98个,翻拍图像中对应的活体数量为88个.文中方法与文献[11],[12]方法的准确率对比,如表1所示.表1中:n为数量.
表1 文中方法与文献[11],[12]方法的准确率对比Tab.1 Accuracy rate comparison of method in this paper with references[11], [12]
由表1可知:文中方法的准确率高于文献[11]方法,但低于文献[12]方法,因此,三通道图像对原图的信息造成了极大的损失.
为保留原图信息,采用特征融合的方式构建卷积神经网络,加入反射图像作为新增加的通道,成为四通道图像.
2.1 CNN基础理论
相比于传统的特征提取方式,深度神经网络(CNN)在同一个特征平面通过同一个卷积核进行卷积处理,权值共享,有效减少权值的数量.通过权值共享,神经元在图像的不同位置能检测到相同的特征,保证图像的平移不变性.同时,通过二维空间中的局部感受,也可以使神经网络从图像的纹理、角点等特征获取更抽象的特征量.
2.2 CNN网络设计
针对图像翻拍检测设计的CNN网络包括两层卷积层,两层池化层与一层全连接层.其中,池化层为最大值池化.在CNN网络中,首先,保留图像的RGB三通道,将新产生的反射图像加入到输入中,作为图像第四层通道进行卷积操作,filter数量为8,卷积核大小为3×3,步长为1,padding方式为same,channel为8;
其次,最大值池化,卷积核大小为2×2,步长为2,再对最大值池化后的图像进行第二次卷积操作,filter数量为16,卷积核大小为3×3,步长为1,padding方式为same;
再次,将卷积操作后的结果进行第2次最大值池化,卷积核大小为2×2,步长为2;
最后,将池化结果展开为一维张量,并通过全连接网络得到最终结果.
2.3 实验分析
2.3.1 新加入特征实验 使用电信营业厅摄像头的真实信息,获取活体数量为947的1 000个样本(正样本为500,负样本为500).每组样本以迭代的形式做5组实验,每组实验迭代4次,每次迭代取收敛后预测集最好的结果,再将这些结果平均值作为最后结果.三通道输入网络的准确率为83.41%;
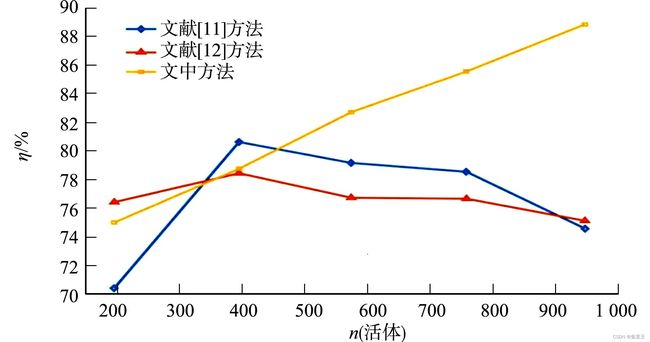
加入特征的四通道输入神经网络的准确率为88.83%.样本数据集,如图13所示.模型准确率随活体数量变化图,如图14所示.
(a) 翻拍图像
图14 模型准确率随活体数量变化图Fig.14 Accuracy of model varies with number of living bodies diagram
由图14可知:加入提取的出反射分量后,较为简单的神经网络获得了更好的准确率,其原因在于深度较小、结构简单的神经网络无法很好地提取复杂的特征(由频率域获得的反射分量特征),通过增加人工特征的方法可以在不增加网络复杂性的情况下提高准确率.相比于直接使用深度神经网络的方式,文中方法可以减少深度神经网络的深度,产生更少的计算复杂度.
2.3.2 特征融合后神经网络稳定性实验 实验使用电信营业厅摄像头的真实信息,获取图像数量为200,400,600,800,1 000的5组样本.
每组样本按8∶2的形式划分为训练集与预测集,训练集以迭代的形式做5组实验,每组实验迭代4次,并对小批量梯度下降进行优化.首先,每次迭代前都重新打乱训练集,更改样本进入顺序.其次,每次迭代选取收敛后的预测集准确率最高的模型.最后,将5个模型对预测集准确率的平均值作为该样本组的实验结果.
根据文献[11],[12]方法训练,对5组样本按8∶2划分为训练集与测试集,并对每组样本相互独立地进行3次实验,将3次实验的平均值作为该样本组的实验结果.
文中方法与文献[11],[12]方法的神经网络稳定性对比,如表2所示.
表2 文中方法与文献[11],[12]方法的神经网络稳定性对比Tab.2 Accuracy rate comparison of neural network stability in this paper with references[11], [12]
由表2可知:当样本数量较小、活体数量较少时,文中方法的神经网络由于样本数量较少,准确率略低于文献[12]方法,但高于文献[11]方法;
当活体数量达到395,正负样本总数达到400时,文献[11],[12]的方法达到收敛;
随着活体数量的增多,样本数量的增加,文献[11],[12]方法的准确率不断下降,而文中方法的3组实验(活体数分别为574,758,947)的准确率保持稳定上升.
文献[11],[12]方法在活体数量较小时有一定的分辨能力,但随着活体数量的增加,训练集复杂情况的提升,适应力较文中方法略有不足.主要原因是翻拍检测的目的均在于检测反射分量,或加强反射分量.文献[11],[12]方法是基于同态补偿的翻拍图像检测,仅仅增强了图像的对比度.提取反射分量特征主要是计算梯度,文献[11],[12]方法对反射分量的特征提取不如文中方法直接,当活体数量较少时,通过增强图像对比度可以强化翻拍图像与真实图像的差别,但当活体数量较多时,由于人脸数量增多及样本量的增加,文献[11],[12]方法不能较好地进行分类,从而无法成功识别翻拍图像.
针对图像翻拍检测,提出了一种通过分离图像反射分量,将其作为新通道加入到原图像,构成四通道简单神经网络的方法.经过实验证明,该方法在硬件设备较低廉,拍摄环境复杂,干扰噪音较多,活体数量较大的环境下,有较高且稳定的准确率、较好的鲁棒性及使用价值.