平衡二叉树及其应用详解
平衡二叉树
定义与性质
平衡二叉树(Balanced Binary Tree)是计算机科学中的一种数据结构,它是二叉排序树的一种特殊情况。
平衡二叉树满足以下性质:
左子树和右子树的高度差不超过 1。也就是说,对于任意节点,其左子树和右子树的高度差不超过 1。
左子树和右子树也都是平衡二叉树。
平衡二叉树的定义可以通过递归的方式来定义。一棵高度为 h 的平衡二叉树,必须满足以下两个条件之一:
该树为空,此时高度为 0。
该树的左子树和右子树都是高度为 h-1 的平衡二叉树。
平衡二叉树的定义保证了树中的每个节点的左右子树的高度差不超过 1,从而使得树的高度比较平衡,便于实现各种操作。
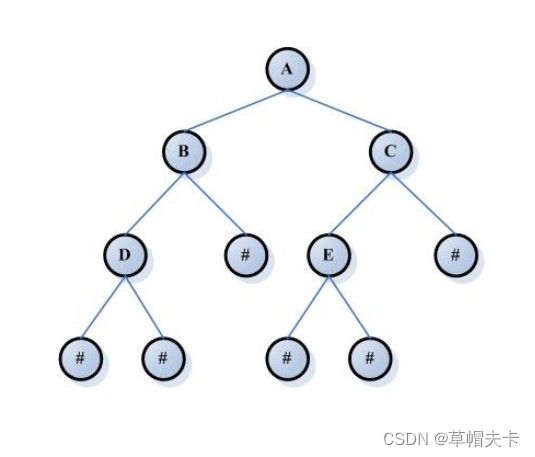
平衡二叉树的应用非常广泛,例如在搜索算法、排序算法、数据结构等领域中都有广泛的应用。由于平衡二叉树的高度比较平衡,因此它具有较好的时间复杂度,特别是对于查找操作,其时间复杂度为 O(logn),其中 n 是树中的节点数。
查找遍历
平衡二叉树的查找遍历有三种基本的方法:前序遍历、中序遍历和后序遍历。
前序遍历(Preorder Traversal):先访问根节点,然后按照先左后右的顺序递归遍历左子树和右子树。
中序遍历(Inorder Traversal):先按照先左后右的顺序递归遍历左子树,然后访问根节点,最后按照先左后右的顺序递归遍历右子树。
后序遍历(Postorder Traversal):先按照先左后右的顺序递归遍历左子树,然后按照先左后右的顺序递归遍历右子树,最后访问根节点。
除了这三种基本的遍历方法,平衡二叉树还有其他的遍历方法,例如层序遍历(Level Order Traversal)、反向遍历(Reverse Traversal)等。不同的遍历方法可以用于不同的应用场景,例如树的打印、树的统计等。
前序遍历
首先,我们需要定义一个平衡二叉树的节点类,包含左右子节点和节点值。然后,实现前序遍历的方法。
以下是平衡二叉树的前序遍历Java代码实现:
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public class BinaryTreePreorderTraversal {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
result.add(node.val);
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
return result;
}
}
这段代码首先定义了一个TreeNode类,用于表示平衡二叉树的节点。然后定义了一个BinaryTreePreorderTraversal类,其中包含一个preorderTraversal方法,用于实现前序遍历。在这个方法中,我们使用了一个栈来辅助遍历,确保遍历的顺序是前序遍历的顺序。
中序遍历
平衡二叉树的中序遍历可以使用递归或迭代的方式实现。以下是使用递归方式实现的代码:
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public class BinaryTreeInorderTraversal {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode curr = root;
while (curr != null || !stack.isEmpty()) {
while (curr != null) {
stack.push(curr);
curr = curr.left;
}
curr = stack.pop();
result.add(curr.val);
curr = curr.right;
}
return result;
}
}
这段代码中,我们首先判断根节点是否为空,如果为空则直接返回一个空的结果列表。然后创建一个栈,并将根节点入栈。接下来进入循环,每次从栈中弹出一个节点,将其值加入结果列表中,并将其右子节点(如果存在)入栈。最后返回结果列表即可。
后序遍历
平衡二叉树的后序遍历可以使用递归或迭代的方式实现。以下是使用递归方式实现的代码:
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public class BinaryTreePostorderTraversal {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
result.add(node.val);
if (node.left != null) {
stack.push(node.left);
}
if (node.right != null) {
stack.push(node.right);
}
}
return result;
}
}
这段代码中,我们首先判断根节点是否为空,如果为空则直接返回一个空的结果列表。然后创建一个栈,并将根节点入栈。接下来进入循环,每次从栈中弹出一个节点,将其值加入结果列表中,并将其左右子节点(如果存在)入栈。最后返回结果列表即可。
插入与删除
平衡二叉树的插入与删除是二叉查找树的重要操作,普通二叉搜索树的操作类似,但是需要通过旋转来保持树的平衡。具体来说,插入或删除一个节点后,需要根据该节点的位置和平衡因子来判断是否需要进行旋转。如果需要进行旋转,则可以分为四种类型:L-L型旋转、L-R型旋转、R-L型旋转和R-R型旋转。这些类型的旋转都有相应的Java代码实现 。
下面是平衡二叉树插入和删除的Java实现:
public class AVLTree {
class Node {
int key, height;
Node left, right;
Node(int d) {
key = d;
height = 1;
}
}
Node root;
// 获取节点高度
int height(Node N) {
if (N == null)
return 0;
return N.height;
}
// 获取两个整数的最大值
int max(int a, int b) {
return (a > b) ? a : b;
}
// 新建一个节点
Node newNode(int key) {
Node node = new Node(key);
node.left = null;
node.right = null;
node.height = 1;
return node;
}
// 右旋转
Node rightRotate(Node y) {
Node x = y.left;
Node T2 = x.right;
x.right = y;
y.left = T2;
y.height = max(height(y.left), height(y.right)) + 1;
x.height = max(height(x.left), height(x.right)) + 1;
return x;
}
// 左旋转
Node leftRotate(Node x) {
Node y = x.right;
Node T2 = y.left;
y.left = x;
x.right = T2;
x.height = max(height(x.left), height(x.right)) + 1;
y.height = max(height(y.left), height(y.right)) + 1;
return y;
}
// 获取平衡因子
int getBalance(Node N) {
if (N == null)
return 0;
return height(N.left) - height(N.right);
}
// 插入节点
Node insert(Node node, int key) {
if (node == null)
return (newNode(key));
if (key < node.key)
node.left = insert(node.left, key);
else if (key > node.key)
node.right = insert(node.right, key);
else // 相等的键不允许在BST中
return node;
node.height = 1 + max(height(node.left), height(node.right));
int balance = getBalance(node);
// 如果节点不平衡,有四种情况需要处理
// 左左型旋转
if (balance > 1 && key < node.left.key)
return rightRotate(node);
// 右右型旋转
if (balance < -1 && key > node.right.key)
return leftRotate(node);
// 左右型旋转
if (balance > 1 && key > node.left.key) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// 右左型旋转
if (balance < -1 && key < node.right.key) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
// 删除节点
Node deleteNode(Node root, int key) {
if (root == null)
return root;
if (key < root.key)
root.left = deleteNode(root.left, key);
else if (key > root.key)
root.right = deleteNode(root.right, key);
else {
if ((root.left == null) || (root.right == null)) {
Node temp = null;
if (temp == root.left)
temp = root.right;
else
temp = root.left;
if (temp == null) {
temp = root;
root = null;
} else
root = temp;
} else {
Node temp = minValueNode(root.right);
root.key = temp.key;
root.right = deleteNode(root.right, temp.key);
}
}
if (root == null)
return root;
root.height = max(height(root.left), height(root.right)) + 1;
int balance = getBalance(root);
// 如果节点不平衡,有四种情况需要处理
// 左左型旋转
if (balance > 1 && getBalance(root.left) >= 0)
return rightRotate(root);
// 右右型旋转
if (balance < -1 && getBalance(root.right) <= 0)
return leftRotate(root);
// 左右型旋转
if (balance > 1 && getBalance(root.left) < 0) {
root.left = leftRotate(root.left);
return rightRotate(root);
}
// 右左型旋转
if (balance < -1 && getBalance(root.right) > 0) {
root.right = rightRotate(root.right);
return leftRotate(root);
}
return root;
}
// 获取最小值节点
Node minValueNode(Node node) {
Node current = node;
while (current.left != null)
current = current.left;
return current;
}
}
复杂度分析
时间复杂度
平衡二叉树的时间复杂度主要取决于插入、删除和查找操作的实现。下面将详细分析这三种操作的时间复杂度。
插入操作:
平衡二叉树的插入操作的时间复杂度为 O(logn),其中 n 是树的节点数量。这是因为插入操作需要在树中找到适当的位置,以保证树的平衡。具体来说,插入操作需要执行以下步骤:
- 将节点插入到树的根节点。
- 如果插入的节点的值比根节点的值小,则将节点插入到根节点的左子树。
- 如果插入的节点的值比根节点的值大,则将节点插入到根节点的右子树。
- 在左子树或右子树中,重复执行步骤 2 和步骤 3,直到找到适当的位置。
在执行插入操作的过程中,最坏情况下需要执行 O(logn)次比较操作,才能找到适当的位置。因此,插入操作的时间复杂度为 O(logn)。
删除操作:
平衡二叉树的删除操作的时间复杂度为 O(logn),其中 n 是树的节点数量。这是因为删除操作需要找到要删除的节点,并在树中进行调整,以保持树的平衡。具体来说,删除操作需要执行以下步骤:
- 找到要删除的节点。
- 如果要删除的节点只有一个孩子节点,则直接将该节点删除,并将该节点的孩子节点替换该节点。
- 如果要删除的节点有两个孩子节点,则需要找到该节点的后继节点,并将该节点的值替换为后继节点的值,然后删除该节点的后继节点。
- 在执行删除操作的过程中,需要对树进行调整,以保持树的平衡。
在执行删除操作的过程中,最坏情况下需要执行 O(logn)次比较操作,才能找到要删除的节点并进行调整。因此,删除操作的时间复杂度为 O(logn)。
查找操作:
平衡二叉树的查找操作的时间复杂度为 O(logn),其中 n 是树的节点数量
空间复杂度
平衡二叉树的空间复杂度主要取决于树的实现方式。下面将详细分析平衡二叉树的空间复杂度。
如果使用数组实现平衡二叉树,则空间复杂度为 O(n),其中 n 是树的节点数量。这是因为数组需要存储树的所有节点,每个节点需要占用一个存储空间。因此,空间复杂度为 O(n)。
如果使用链表实现平衡二叉树,则空间复杂度为 O(n),其中 n 是树的节点数量。这是因为链表需要存储树的所有节点,每个节点需要占用一个存储空间。因此,空间复杂度为 O(n)。
如果使用递归实现平衡二叉树,则空间复杂度为 O(logn),其中 n 是树的节点数量。这是因为递归实现需要使用栈来存储递归调用的上下文,每次递归调用需要占用一个栈帧,因此空间复杂度为 O(logn)。
总的来说,平衡二叉树的空间复杂度取决于树的实现方式。如果使用数组或链表实现平衡二叉树,则空间复杂度为 O(n),其中 n 是树的节点数量。如果使用递归实现平衡二叉树,则空间复杂度为 O(logn),其中 n 是树的节点数量。
应用场景
平衡二叉树的应用场景如下:
- 排序:平衡二叉树可以作为一种排序算法,例如堆排序和快速排序。通过维护一个平衡二叉树,可以快速地对数据进行排序。
- 查找:平衡二叉树可以作为一种查找算法,例如二叉查找树。通过维护一个平衡二叉树,可以快速地在树中查找特定的节点。
- 数据结构:平衡二叉树可以作为一种数据结构,例如红黑树。红黑树是一种特殊的平衡二叉树,它具有以下特点:
- 每个节点要么是红色,要么是黑色。
- 根节点是黑色。
- 每个叶子节点(NIL 节点,空节点)是黑色。
- 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
红黑树在实际应用中非常广泛,例如在操作系统、数据库、图形学等领域中都有广泛的应用。(下一篇将对红黑树做出详细介绍)