Matlab(基本操作与矩阵输入)
目录
1.Matlab视窗详读
2.基本操作与矩阵输入
2.1 运算符的优先级
2.2 初等数学函数
2.3 嵌入函数
2.4 特殊变量和常量
2.5 Matlab的优先级调用
2.6 数字显示格式长
2.7 命令行中端
2.8 部分函数
2.9 向量和矩阵
2.10 数组索引
2.11 串联矩阵
2.12 生成数值序列
2.13 矩阵相关的函数
作为一名数学专业的学生,掌握Matlab也是非常重要的,接下来分享在学习Matlab中记录的笔记供大家分享!!!
在这里可能没有接触过Matlab的同学并不了解这是什么东西,我们首先对Matlab做一下简单的科普:Matlab是一种高级的计算机编程语言和环境,用于数值计算、数据可视化和算法开发,它具有强大的矩阵操作能力和丰富的数值计算函数库,适用于科学计算、工程分析、数据处理和机器学习等领域。Matlab还提供了一套图形用户界面工具,方便用户进行交互的数据分析和可视化操作。
Matlab帮助文档
1.Matlab视窗详读
2.基本操作与矩阵输入
2.1 运算符的优先级
- 括号()
- 幂 ^
- 乘除 * /
- 加减 + -
2.2 初等数学函数
- 基本算术
| + | 添加数字,追加字符串 |
| sum | 数组元素总和 |
| cumsum | 累加和 |
| movsum | 移动总和 |
案例:
| - | 减法 |
| diff | 差分和近似导数 |
案例:
| .* | 乘法 |
| * | 矩阵乘法 |
| prod | 数组元素的乘积 |
| cumprod | 累积乘积 |
案例:
*:
.*:
prod:
| .\ | 数组右除 |
| .\ | 数组左除 |
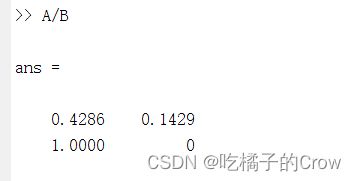
| / | 求解xA=B |
| \ | 求解Ax=B |
在矩阵中左除(乘)和右除(乘)是有区别的,不了解的同学可自行查看资料
原数组:
./:
.\:
/:
\:
- 模除法和舍入
| mod | 除后的余数(取模运算) |
| rem | 除后的余数 |
| idivide | 带有舍入选项的整数 |
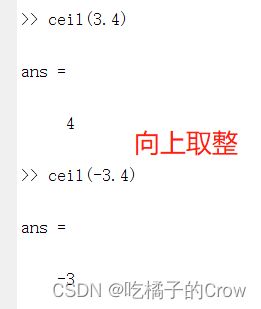
| ceil | 向正无穷舍入 |
| fix | 向零舍入 |
| floor | 向负无穷舍入 |
| round | 舍入至最近的小数或整数 |
案例:
mod:
%b = mod(a,m) 返回 a 除以 m 后的余数,其中 a 是被除数,m 是除数。此函数通常称为取模运算,表达式为 b = a - m.*floor(a./m)。mod 函数遵从 mod(a,0) 返回 a 的约定。
b=mod(a,m)rem:
%r = rem(a,b) 返回 a 除以 b 后的余数,其中 a 是被除数,b 是除数。此函数通常称为求余运算,表达式为 r = a - b.*fix(a./b)。rem 函数遵从 rem(a,0) 是 NaN 的约定。
r=rem(a,b)ceil:
fix:
floor:
round:
- 指数和对数
| exp | 指数 |
| log | 自然对数 |
| log10 | 常用对数(以10为底) |
| sqrt | 平方根 |
2.3 嵌入函数
2.4 特殊变量和常量
- ans :结果
- i,j :复数
0.0000 + 1.0000i- Inf :无穷大
Inf- eps : 2.2204e-16
2.2204e-16- NaN:not a number
NaN- pi : π
3.1416我们也可以通过iskeyword快速查看文档哪些是特殊的变量以及常量
2.5 Matlab的优先级调用
2.6 数字显示格式长
| short | Short,结果小数点后有4位的短的固定十进制格式 |
| long | Long,固定的十进制格式,双值在小数点后15位,单值在小数点后7位 |
| shortE | 小数点后有4位数的短科学计数法 |
| longE | 长科学计数法,双值在小数点后15位,单值在小数点后7位 |
| bank | 小数点后有两位的货币格式 |
| hex | 二进制双精度数的十六进制表示 |
| rat | 小整数的比率,将数值转成有理数、分数 |
案例:
>> format long
>> pi
ans =
3.141592653589793
>> format short
>> pi
ans =
3.1416
>> format shortE
>> pi
ans =
3.1416e+00
>> format longE
>> pi
ans =
3.141592653589793e+00
>> format bank
>> pi
ans =
3.14
>> format hex
>> pi
ans =
400921fb54442d18
>> format rat
>> pi
ans =
355/113 2.7 命令行中端
我们输入几行命令,看有;和无;有什么区别:
>> A=[1 2 3];
>> >> B=[2 2 2]
B =
2 2 2 简单来说,;在命令的末尾会抑制终端的输出
2.8 部分函数
| clc | 清除命令窗口显示 |
| clear | 删除工作区中所有的变量,从工作区中删除项目、释放系统内存 |
| who | 列出工作区中的变量 |
| whos | 列出工作区中的变量及大小和类型 |
>> who
您的变量为:
A B C D ans b cos
>> whos
Name Size Bytes Class Attributes
A 1x3 24 double
B 1x3 24 double
C 1x2 16 int64
D 1x2 16 int64
ans 1x1 8 double
b 1x1 8 double
cos 1x11 22 char 2.9 向量和矩阵
一些特殊的矩阵:
- linspace():生成线性间距向量
- eye():单位矩阵
- zeros():创建全零矩阵
- diag():创建对角矩阵或获取矩阵的对角元素
- rand():均匀分布随机数
- magic():魔方矩阵
- ones():创建全一矩阵
>> A=[1 2 3 4]
A =
1 2 3 4
>> B=[1;2;3;4]
B =
1
2
3
4
>> C=[1 2;3 4]
C =
1 2
3 4
>> D=rand(3,4)%随机矩阵
D =
664/815 717/785 408/1465 687/712
1298/1433 1493/2361 1324/2421 589/3737
751/5914 694/7115 338/353 6271/6461
>> E=ones(3,4)%单位矩阵
E =
1 1 1 1
1 1 1 1
1 1 1 1
>> F=eye(3,4)%对角线为1的矩阵
F =
1 0 0 0
0 1 0 0
0 0 1 0
>> G=magic(5)%魔方矩阵 行、列、对角线乘积相同的矩阵
G =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
>> zeros(3,4)%零矩阵
ans =
0 0 0 0
0 0 0 0
0 0 0 0
2.10 数组索引
G =
8 1 6
3 5 7
4 9 2
>> G(7)%数组中第7个元素
ans =
6
>> G([1 4 9])%数组中第1、4、9个元素
ans =
8 1 2
>> G([2 3;2 3])%数组中第2、3个元素和2、3个元素组成的矩阵
ans =
3 4
3 4
>> G([2 3],[2 3])%第2、3行与第2、3列的交集组成的矩阵
ans =
5 7
9 2 假如若要修改数组中的元素,可以用:
>> G(1,3)=10%第1行第3列的元素修改为10
G =
8 1 10
3 5 7
4 9 2 如果要输出某一行或者是某一列,则:
>> G(1,:)%输出第一行的全部元素
ans =
8 1 10
>> G(:,1)%输出第一列的全部元素
ans =
8
3
4 2.11 串联矩阵
我们可以使用方括号来追加现有的矩阵,这种创建矩阵的方式称为串联,例:
如果要合并为一行的话:
>> A=ones(1,3)
A =
1 1 1
>> B=rand(1,3)
B =
581/607 614/1265 1142/1427
>> C=[A B]
C =
1 1 1 581/607 614/1265 1142/1427
如果要合并为两行的话:
>> C=[A;B]
C =
1 1 1
581/607 614/1265 1142/1427 要串联多个矩阵的时候,它们必须要有兼容的大小,水平串联时,它们的行数必须相同,垂直串联时,它们的列数必须相同
我们在串联的时候也可以使用函数horzcat()进行操作:
水平串联:
>> D=horzcat(A,B)
D =
1 1 1 581/607 614/1265 1142/1427 垂直串联:
>> D=vertcat(A,B)
D =
1 1 1
581/607 614/1265 1142/1427 2.12 生成数值序列
- 创建一个行向量,其元素是从1到10的整数
A=1:10
>> A=1:10
A =
列 1 至 7
1 2 3 4 5 6 7
列 8 至 10
8 9 10 - 可以用冒号运算符创建在任何范围内以1为增量的数字序列
>> A=1:-2:-8
A =
1 -1 -3 -5 -7 >> 1:-2:8%起点和终点必须合法
ans =
空的 1×0 double 行向量2.13 矩阵相关的函数
>> A=[2 5 6;1 5 6;9 2 1]
A =
2 5 6
1 5 6
9 2 1- max(A)
%A为向量:返回的是A的最大值
%A为矩阵:返回的是每列的最大值
>> max(A)
ans =
9 5 6 - max(max(A))
%返回的是A中的最大值
>> max(max(A))
ans =
9 - sum(A)
%返回每列的元素之和
>> sum(A)
ans =
12 12 13
%返回矩阵的所有元素之和
>> sum(sum(A))
ans =
37 - sort(A)
%每列进行排序(从小到大)
>> sort(A)
ans =
1 2 1
2 5 6
9 5 6 - sortrows(A)
%对矩阵行或者表进行排序,基于第一列中的元素按升序对矩阵进行排序
>> sortrows(A)
ans =
1 5 6
2 5 6
9 2 1 - size(A)
%得出该矩阵时几行几列
>> size(A)
ans =
3 3 - find(A)
%查找非零元素的索引和值
>> find(A)
ans =
1
2
3
4
5
6
7
8
9
%如果在数组中有多个元素符合,则输出
>> find(A==5)
ans =
4
5
%对于在数组中不存在的元素,直接输出空向量
>> find(A==11)
ans =
空的 0×1 double 列向量