ViT论文Pytorch代码解读
ViT论文代码实现
论文地址:https://arxiv.org/abs/2010.11929
Pytorch代码地址:https://github.com/lucidrains/vit-pytorch
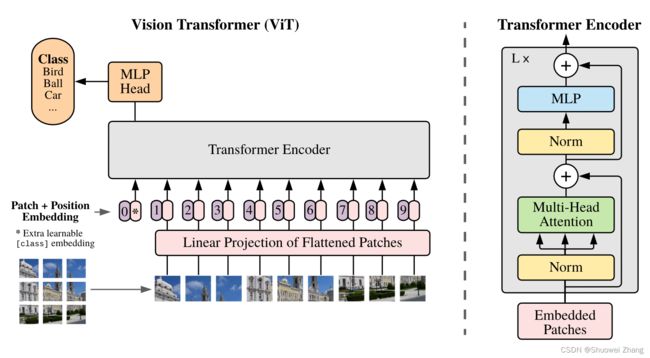
ViT结构图
调用代码
import torch
from vit_pytorch import ViT
def test():
v = ViT(
image_size = 256,
patch_size = 32,
num_classes = 1000,
dim = 1024,
depth = 6,
heads = 16,
mlp_dim = 2048,
dropout = 0.1,
emb_dropout = 0.1
)
img = torch.randn(1, 3, 256, 256)
preds = v(img)
print(preds.shape)
assert preds.shape == (1, 1000), 'correct logits outputted'
if __name__ == '__main__':
test()
ViT结构
class ViT(nn.Module):
def __init__(self, *, image_size, patch_size, num_classes, dim, depth, heads, mlp_dim, pool='cls', channels=3,
dim_head=64, dropout=0., emb_dropout=0.):
super().__init__()
# 将image_size和patch_size都转换为(height, width)形式
image_height, image_width = pair(image_size)
patch_height, patch_width = pair(patch_size)
# 检查图像尺寸是否可以被patch尺寸整除
assert image_height % patch_height == 0 and image_width % patch_width == 0, 'Image dimensions must be divisible by the patch size.'
# 计算图像中的patch数量
num_patches = (image_height // patch_height) * (image_width // patch_width)
# 计算每个patch的维度(即每个patch的元素数量)
patch_dim = channels * patch_height * patch_width
# 确保池化方式是'cls'或'mean'
assert pool in {'cls', 'mean'}, 'pool type must be either cls (cls token) or mean (mean pooling)'
# 将图像转换为patch嵌入的操作
self.to_patch_embedding = nn.Sequential(
Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=patch_height, p2=patch_width), # 图像切分重排,后文有注释
# 注:此时的维度为[b, h*w/p1/p2, p1*p2*c]:[批处理尺寸、图像中patch的数、每个patch的元素数量]
nn.LayerNorm(patch_dim), # 对patch进行层归一化
nn.Linear(patch_dim, dim), # 使用线性层将patch的维度从patch_dim转化为dim
nn.LayerNorm(dim), # 对结果进行层归一化
)
self.pos_embedding = nn.Parameter(torch.randn(1, num_patches + 1, dim)) # 初始化位置嵌入
self.cls_token = nn.Parameter(torch.randn(1, 1, dim)) # 初始化CLS token(用于分类任务的特殊token)
self.dropout = nn.Dropout(emb_dropout)
self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim, dropout) # 定义Transformer模块
self.pool = pool # 设置池化方式('cls'或'mean')
self.to_latent = nn.Identity() # 设置一个恒等映射(在此实现中不改变数据,但可以在子类或其他变种中进行修改)
self.mlp_head = nn.Linear(dim, num_classes) # 定义MLP头部,用于最终的分类
def forward(self, img):
x = self.to_patch_embedding(img) # 第一步,将图片切分为若干小块
# 此时维度为:[b, h*w/p1/p2, dim]
b, n, _ = x.shape
# 第二步,设置位置编码
cls_tokens = repeat(self.cls_token, '1 1 d -> b 1 d', b=b) # 将cls_token复制b个
# (为每个输入图像复制一个CLS token,使输入批次中的每张图像都有一个相应的CLS token)
x = torch.cat((cls_tokens, x), dim=1) # 将CLS token与patch嵌入合并; cat之后,原来的维度[1,64,1024],就变成了[1,65,1024]
x += self.pos_embedding[:, :(n + 1)] # 原数据和位置编码直接进行相加操作,即完成结构图中的【Patch + Position Embedding】操作
x = self.dropout(x)
# 第三步,Transformer的Encoder结构
x = self.transformer(x)
x = x.mean(dim=1) if self.pool == 'mean' else x[:, 0] # 根据所选的池化方式进行池化
x = self.to_latent(x) # 将数据传递给恒等映射
return self.mlp_head(x) # 使用MLP头部进行分类
Rearrange解释:
y = x.transpose(0, 2, 3, 1)
可以写成:y = rearrange(x, ‘b c h w -> b h w c’)
关于pos_embedding和cls_token的逻辑讲解:
如图所示,红色框框出的部分。
图像被切分为多个小块之后,经过self.to_patch_embedding中的Rearrange,原本的[b,c,h,w]维度变为[b, h*w/p1/p2, p1*p2*c]。
再经过线性层nn.Linear(patch_dim, dim),维度变为[b, h*w/p1/p2, dim]。
输出结果即为上图中黄色框标出的部分的粉色条(不包括紫色条,是因为此处还没进行Position Embedding操作)。
继续往下走,进行torch.cat((cls_tokens, x), dim=1),此时将x与cls_tokens进行concat操作,得到红色框框出的所有粉色条(在原本的基础上增加了带*号的粉色条)。
记下来的x += self.pos_embedding[:, :(n + 1)]操作就是将x与pos_embedding直接进行相加,用图表示出来就是上图中整个红色框框出的部分了(紫色条就是传说中的pos_embedding)。
举一个有数字的例子:
原本输入图像维度为[1, 3, 256, 256],dim设置为1023,经过self.to_patch_embedding后维度变为:[1,64,1024],cls_tokens的维度为:[1,1,1024],经过concat操作后,x的维度变为[1,65,1024],然后经过pos_embedding加操作后,维度依然是[1,65,1024],因为在设置变量pos_embedding时的维度就是torch.randn(1, num_patches + 1, dim)。
~这个解释应该够清晰了吧!~
Transformer Encoder结构
# 定义前馈神经网络
class FeedForward(nn.Module):
def __init__(self, dim, hidden_dim, dropout=0.):
super().__init__()
self.net = nn.Sequential(
# Vit_base: dim=768,hidden_dim=3072
nn.LayerNorm(dim),
nn.Linear(dim, hidden_dim), # 将输入从dim维映射到hidden_dim维
nn.GELU(),
nn.Dropout(dropout),
nn.Linear(hidden_dim, dim), # 将隐藏状态从hidden_dim维映射回到dim维
nn.Dropout(dropout)
)
def forward(self, x):
return self.net(x)
class Attention(nn.Module):
def __init__(self, dim, heads=8, dim_head=64, dropout=0.):
super().__init__()
inner_dim = dim_head * heads # 64*8=512 # 计算内部维度
project_out = not (heads == 1 and dim_head == dim) # 判断是否需要投影输出,投影输出就是是否需要经过线性层
# 如果只有一个attention头并且其维度与输入相同则不需要投影输出,否则需要。
self.heads = heads
self.scale = dim_head ** -0.5 # 缩放因子,通常是头维度的平方根的倒数
self.norm = nn.LayerNorm(dim)
self.attend = nn.Softmax(dim=-1) # softmax函数用于最后一个维度,计算注意力权重
self.dropout = nn.Dropout(dropout)
self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False) # 一个线性层生成Q, K, V
# 判断是否需要投影输出
self.to_out = nn.Sequential(
nn.Linear(inner_dim, dim),
nn.Dropout(dropout)
) if project_out else nn.Identity()
def forward(self, x):
x = self.norm(x)
qkv = self.to_qkv(x).chunk(3, dim=-1) # 用线性层生成QKV,并在最后一个维度上分块;相当于写3遍nn.Linear
q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h=self.heads), qkv)
# 将[batch_size, sequence_length, heads_dimension] 转换为 [batch_size, number_of_heads, sequence_length, dimension_per_head]
dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale # 计算Q和K的点乘,然后进行缩放
# q: [batch_size, number_of_heads, sequence_length, dimension_per_head]
# k转置后:[batch_size, number_of_heads, sequence_length, dimension_per_head] -> [batch_size, number_of_heads, dimension_per_head, sequence_length]
# q和k点乘后:[batch_size, number_of_heads, sequence_length, sequence_length]
attn = self.attend(dots) # 使用softmax函数获取注意力权重
attn = self.dropout(attn)
# 使用注意力权重对V进行加权
out = torch.matmul(attn, v)
out = rearrange(out, 'b h n d -> b n (h d)') # 使用rearrange函数重新组织输出的维度
return self.to_out(out) # 投影输出(如果需要)
class Transformer(nn.Module):
def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout=0.):
super().__init__()
self.norm = nn.LayerNorm(dim)
self.layers = nn.ModuleList([])
for _ in range(depth): # depth设置为几层,就重复几次
self.layers.append(nn.ModuleList([
Attention(dim, heads=heads, dim_head=dim_head, dropout=dropout),
FeedForward(dim, mlp_dim, dropout=dropout)
]))
def forward(self, x):
for attn, ff in self.layers: # 残差
x = attn(x) + x
x = ff(x) + x
return self.norm(x)
如上就是ViT的整体结构了。
附:完整代码
import torch
from torch import nn
from einops import rearrange, repeat
from einops.layers.torch import Rearrange
# helpers
def pair(t):
return t if isinstance(t, tuple) else (t, t)
# classes
class FeedForward(nn.Module):
def __init__(self, dim, hidden_dim, dropout=0.):
super().__init__()
self.net = nn.Sequential(
# Vit_base: dim=768,hidden_dim=3072
nn.LayerNorm(dim),
nn.Linear(dim, hidden_dim),
nn.GELU(),
nn.Dropout(dropout),
nn.Linear(hidden_dim, dim),
nn.Dropout(dropout)
)
def forward(self, x):
return self.net(x)
class Attention(nn.Module):
def __init__(self, dim, heads=8, dim_head=64, dropout=0.):
super().__init__()
inner_dim = dim_head * heads # 64*8=512
project_out = not (heads == 1 and dim_head == dim)
self.heads = heads
self.scale = dim_head ** -0.5
self.norm = nn.LayerNorm(dim)
self.attend = nn.Softmax(dim=-1)
self.dropout = nn.Dropout(dropout)
self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False)
self.to_out = nn.Sequential(
nn.Linear(inner_dim, dim),
nn.Dropout(dropout)
) if project_out else nn.Identity()
def forward(self, x):
x = self.norm(x)
qkv = self.to_qkv(x).chunk(3, dim=-1) # 相当于写3遍nn.Linear
q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h=self.heads), qkv)
# 将[batch_size, sequence_length, heads_dimension] 转换为 [batch_size, number_of_heads, sequence_length, dimension_per_head]
dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale
# q: [batch_size, number_of_heads, sequence_length, dimension_per_head]
# k转置后:[batch_size, number_of_heads, sequence_length, dimension_per_head] -> [batch_size, number_of_heads, dimension_per_head, sequence_length]
# q和k点乘后:[batch_size, number_of_heads, sequence_length, sequence_length]
attn = self.attend(dots)
attn = self.dropout(attn)
out = torch.matmul(attn, v)
out = rearrange(out, 'b h n d -> b n (h d)')
return self.to_out(out)
class Transformer(nn.Module):
def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout=0.):
super().__init__()
self.norm = nn.LayerNorm(dim)
self.layers = nn.ModuleList([])
for _ in range(depth):
self.layers.append(nn.ModuleList([
Attention(dim, heads=heads, dim_head=dim_head, dropout=dropout),
FeedForward(dim, mlp_dim, dropout=dropout)
]))
def forward(self, x):
for attn, ff in self.layers:
x = attn(x) + x
x = ff(x) + x
return self.norm(x)
class ViT(nn.Module):
def __init__(self, *, image_size, patch_size, num_classes, dim, depth, heads, mlp_dim, pool='cls', channels=3,
dim_head=64, dropout=0., emb_dropout=0.):
super().__init__()
image_height, image_width = pair(image_size)
patch_height, patch_width = pair(patch_size)
assert image_height % patch_height == 0 and image_width % patch_width == 0, 'Image dimensions must be divisible by the patch size.'
num_patches = (image_height // patch_height) * (image_width // patch_width)
patch_dim = channels * patch_height * patch_width
assert pool in {'cls', 'mean'}, 'pool type must be either cls (cls token) or mean (mean pooling)'
self.to_patch_embedding = nn.Sequential(
Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=patch_height, p2=patch_width), # 图像切分重排
nn.LayerNorm(patch_dim),
nn.Linear(patch_dim, dim),
nn.LayerNorm(dim),
)
# Rearrange解释:
# y = x.transpose(0, 2, 3, 1)
# 可以写成:y = rearrange(x, 'b c h w -> b h w c')
self.pos_embedding = nn.Parameter(torch.randn(1, num_patches + 1, dim))
self.cls_token = nn.Parameter(torch.randn(1, 1, dim))
self.dropout = nn.Dropout(emb_dropout)
self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim, dropout)
self.pool = pool
self.to_latent = nn.Identity()
self.mlp_head = nn.Linear(dim, num_classes)
def forward(self, img):
x = self.to_patch_embedding(img)
b, n, _ = x.shape
cls_tokens = repeat(self.cls_token, '1 1 d -> b 1 d', b=b) # 数字编码,将cls_token复制b个
x = torch.cat((cls_tokens, x), dim=1) # cat之后,原来的维度[1,64,1024],就变成了[1,65,1024]
x += self.pos_embedding[:, :(n + 1)]
x = self.dropout(x)
x = self.transformer(x)
x = x.mean(dim=1) if self.pool == 'mean' else x[:, 0]
x = self.to_latent(x)
return self.mlp_head(x)
附:训练代码
model = ViT(
dim=128,
image_size=224,
patch_size=32,
num_classes=2,
transformer=efficient_transformer,
channels=3,
).to(device)
# loss function
criterion = nn.CrossEntropyLoss()
# optimizer
optimizer = optim.Adam(model.parameters(), lr=lr)
# scheduler
scheduler = StepLR(optimizer, step_size=1, gamma=gamma)
for epoch in range(epochs):
epoch_loss = 0
epoch_accuracy = 0
for data, label in tqdm(train_loader):
data = data.to(device)
label = label.to(device)
output = model(data)
loss = criterion(output, label)
optimizer.zero_grad()
loss.backward()
optimizer.step()
acc = (output.argmax(dim=1) == label).float().mean()
epoch_accuracy += acc / len(train_loader)
epoch_loss += loss / len(train_loader)
with torch.no_grad():
epoch_val_accuracy = 0
epoch_val_loss = 0
for data, label in valid_loader:
data = data.to(device)
label = label.to(device)
val_output = model(data)
val_loss = criterion(val_output, label)
acc = (val_output.argmax(dim=1) == label).float().mean()
epoch_val_accuracy += acc / len(valid_loader)
epoch_val_loss += val_loss / len(valid_loader)
print(
f"Epoch : {epoch+1} - loss : {epoch_loss:.4f} - acc: {epoch_accuracy:.4f} - val_loss : {epoch_val_loss:.4f} - val_acc: {epoch_val_accuracy:.4f}\n"
)