【算法与数据结构】112、LeetCode路径总和

所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

一、题目

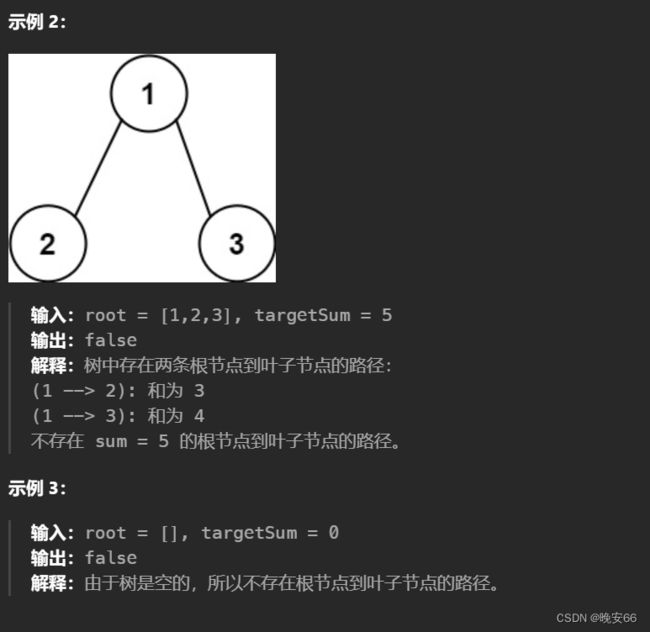
二、解法

  思路分析：本题通过计算根节点到叶子节点路径上节点的值之和，然后再对比目标值。利用文章【算法和数据结构】257、LeetCode二叉树的所有路径中的递归算法。这里要注意，默认路径之和是不等于目标值，一旦递归当中出现了等于的情况就直接返回，不必继续算后面的和。因此程序当中将结果result作为引用输入参数，有true出现就直接退出了。
  程序如下：

class Solution {
public:          
    void traversal(TreeNode* root, int sumOfPath, const int targetSum, bool &result) {
        // 1.输入参数和返回值 
        sumOfPath += root->val;

        // 2.终止条件：遇到叶子节点
        if (!root->left && !root->right) {
            if (sumOfPath == targetSum) result = true;
        }

        // 3.单层递归逻辑：递归+回溯
        if (root->left && !result)  traversal(root->left, sumOfPath, targetSum, result);    // 左                         
        if (root->right && !result) traversal(root->right, sumOfPath, targetSum, result);  // 右
    }

    bool hasPathSum(TreeNode* root, int targetSum) {
        bool result = false;
        if(root) traversal(root, 0, targetSum, result);
        return result;
    }
};

复杂度分析：

• 时间复杂度： $O(n)$。
• 空间复杂度：$O(n)$。

三、完整代码

# include 
# include 
# include 
# include 
# include 
# include 
using namespace std;

// 树节点定义
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};

class Solution {
public:          
    void traversal(TreeNode* root, int sumOfPath, const int targetSum, bool &result) {
        // 1.输入参数和返回值 
        sumOfPath += root->val;

        // 2.终止条件：遇到叶子节点
        if (!root->left && !root->right) {
            if (sumOfPath == targetSum) result = true;
        }

        // 3.单层递归逻辑：递归+回溯
        if (root->left && !result)  traversal(root->left, sumOfPath, targetSum, result);    // 左                         
        if (root->right && !result) traversal(root->right, sumOfPath, targetSum, result);  // 右
    }

    bool hasPathSum(TreeNode* root, int targetSum) {
        bool result = false;
        if(root) traversal(root, 0, targetSum, result);
        return result;
    }
};

template<typename T>
void my_print(T& v, const string msg)
{
    cout << msg << endl;
    for (class T::iterator it = v.begin(); it != v.end(); it++) {
        cout << *it << ' ';
    }
    cout << endl;
}

template<class T1, class T2>
void my_print2(T1& v, const string str) {
    cout << str << endl;
    for (class T1::iterator vit = v.begin(); vit < v.end(); ++vit) {
        for (class T2::iterator it = (*vit).begin(); it < (*vit).end(); ++it) {
            cout << *it << ' ';
        }
        cout << endl;
    }
}

// 前序遍历迭代法创建二叉树，每次迭代将容器首元素弹出（弹出代码还可以再优化）
void Tree_Generator(vector<string>& t, TreeNode*& node) {
    if (!t.size() || t[0] == "NULL") return;    // 退出条件
    else {
        node = new TreeNode(stoi(t[0].c_str()));    // 中
        if (t.size()) {
            t.assign(t.begin() + 1, t.end());
            Tree_Generator(t, node->left);              // 左
        }
        if (t.size()) {
            t.assign(t.begin() + 1, t.end());
            Tree_Generator(t, node->right);             // 右
        }
    }
}

// 层序遍历
vector<vector<int>> levelOrder(TreeNode* root) {
    queue<TreeNode*> que;
    if (root != NULL) que.push(root);
    vector<vector<int>> result;
    while (!que.empty()) {
        int size = que.size();  // size必须固定, que.size()是不断变化的
        vector<int> vec;
        for (int i = 0; i < size; ++i) {
            TreeNode* node = que.front();
            que.pop();
            vec.push_back(node->val);
            if (node->left) que.push(node->left);
            if (node->right) que.push(node->right);
        }
        result.push_back(vec);
    }
    return result;
}

// 二叉树所有路径
class Solution2 {
public:
    // 前序遍历递归法:精简版本      
    void traversal(TreeNode* root, string path, vector<string>& result) { // 1.输入参数和返回值        
        path += to_string(root->val);      // 中间节点先加入path
        if (!root->left && !root->right) {  // 2.终止条件：遇到叶子节点
            result.push_back(path);
            return;
        }
        // 3.单层递归逻辑：递归+回溯
        if (root->left) traversal(root->left, path + "->", result);     // 左
        if (root->right) traversal(root->right, path + "->", result);   // 右
    }
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        if (!root) return result;
        traversal(root, "", result);
        return result;
    }
};

int main()
{
    vector<string> t = { "5", "4", "11", "7", "NULL", "NULL", "2", "NULL", "NULL", "NULL", "8", "13", "NULL", "NULL", "4", "NULL", "1", "NULL", "NULL"};   // 前序遍历
    my_print(t, "目标树");
    TreeNode* root = new TreeNode();
    Tree_Generator(t, root);
    vector<vector<int>> tree = levelOrder(root);
    my_print2<vector<vector<int>>, vector<int>>(tree, "目标树:");

    Solution2 s2;
    vector<string> path = s2.binaryTreePaths(root);
    my_print(path, "所有路径为：");

    Solution s;
    int targetSum = 22;
    bool result = s.hasPathSum(root, targetSum);
    cout << "路径总和是否满足目标值：  " << result << endl;
    system("pause");
    return 0;
}

end