Learning to Enhance Low-Light Image via Zero-Reference Deep Curve Estimation

学习目标：

1. Learning to Enhance Low-Light Image
   via Zero-Reference Deep Curve Estimation（零参考深度曲线估计）

---

个人体会：

本文的特色就是使用了PA和CA,对不同通道和不同像素做不同处理,虽然本文的实现过程懂了,但是实现去雾的原理不懂,不明白为什么经过一些的卷积操作,残差链接就实现了图像去雾

---

知识点：

Retinex理论
Gray-World color constancy hypothesis
深度可分离卷积

---

内容解读：

1. 摘要：

本文提出零参考深度曲线估计(Zero-DCE)，用于弱光图像增强。本文方法训练一个轻量级的深度网络DCE-Net，以弱光图像为输入，以高阶曲线为输出，然后利用这些曲线对输入图像进行像素级调整，以获得增强的图像。该曲线估计是专门设计的,考虑像素值范围、单调性和可微性。Zero-DCE在其对参考图像的宽松假设方面是有吸引力的，贡献在是第一个不依赖于成对和非成对训练数据的弱光增强网络，这是通过一组精心制定的非参考损耗函数实现的，该函数隐含地测量增强质量并驱动网络学习。尽管其简单，研究表明它很好地适用于不同的照明条件。我们的方法是有效的，因为图像增强可以通过直观和简单的非线性曲线映射。
我们的基于深度学习方法的独特优势，即在训练过程中不需要任何配对或甚至不配对的数据。这就使得可以通过一组专门设计的非参考损耗函数包括空间一致性损失、曝光控制损失、颜色恒定性损失和照明平滑度损失，所有这些考虑到光增强的多因素里。
主要贡献如下：

• 不依赖于成对和非成对训练数据的弱光增强网络，从而避免了过拟合的风险。适应于各种照明条件
• 设计了一个特定于图像的曲线，它能够通过迭代应用自身来逼近像素级和高阶曲线。这样的图像特定曲线可以在很宽的动态范围内有效地进行映射。
• 通过间接评估增强质量的特定于任务的非参考损失函数展示了在没有参考图像的情况下训练深度图像增强模型的潜力

以弱光图像为输入，以高阶曲线为输出，然后利用这些曲线对输入图像进行像素级调整，以获得增强的图像。曲线估算经过精心制定，因此它保持增强图像的范围并保持相邻像素的对比度。重要的是，它是可微分的，并且因此我们可以通过深度卷积神经网络去调整参数。拟建网络为轻重量的，设计曲线可迭代应用于近似高阶曲线以获得更鲁棒和准确的动态范围调整。

2.相关工作

3.方法

Zero-DCE的框架

设计了一种深度曲线估计网络(DCE-Net)来估计一组给定输入图像的最佳拟合光增强曲线(LE-曲线)。然后，该框架通过迭代应用曲线来映射输入的RGB通道的所有像素，以获得最终增强的图像。

3.1 光增强曲线

受照片编辑软件中使用的曲线调整的启发，我们设计了一种可以将弱光图像自动映射到正常光照的曲线，其中自适应曲线参数完全取决于输入图像。设计这种曲线需要满足三个标准

（为什么有这1,2两条标准）：

1. 增强图像的每个像素值应落在[0,1]的范围内，以避免溢出截断引起的信息丢失；
2. 这条曲线应该是单调的，以保持相邻像素的差异（对比度）；
3. 在梯度反向传播的过程中，这条曲线的形式应该尽可能简单和可微。

为了实现这三个目标，我们设计了一条二次曲线，可以表示为：

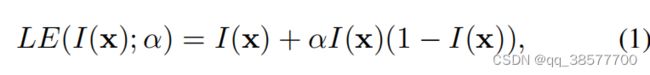
其中x表示像素坐标，LE(I(x);α)是给定输入I(x)的增强版本，可训练曲线参数α∈[-1,1]调整LE曲线的大小并控制暴露水平。输入的每个像素都被归一化为[0,1] 的范围，并且所有操作都是逐像素的（每个颜色通道具有单独的曲线）。我们将LE曲线分别应用于三个RGB通道，而不是仅应用于亮度通道。三通道调节可以更好地保留固有颜色，降低过饱和风险。我们在消融研究中报道了更多细节。具有不同调整参数α的LE曲线如图2(b)所示。显然，LE曲线符合上述三个目标。因此，增强图像的每个像素值在[0，1]的范围内。此外，LE曲线使我们能够增加或减小输入图像的动态范围。这种能力不仅有利于增强弱光区域，还有助于消除过度曝光伪影。我们选择一种特殊的单参数形式作为二次型，因为：

• 1)单参数形式可以减少计算量，提高算法的速度；
• 2)专门设计的二次型满足设计的三个目标，并且已经取得了令人满意的增强性能。

（1)式的基础上，我们发现通过使用迭代的思路来进行高序曲线（High Order Curve）增强与逐像素曲线（Pixel-wise Curve）增强可以使得性能进一步增强。因此最终光照增强曲线公式如下：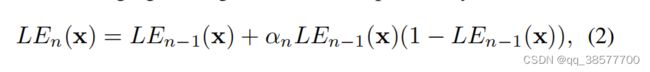
其中n是控制曲率的迭代次数。在本文中，我们将n值设置为8，它可以很好地处理大多数情况。当方程(2)n等于1时，方程(2)可以退化为方程(1)。图2©提供了一个例子，显示了具有不同α和n的高次曲线。这种高次曲线提供了比图2(b)中的曲线更强大的调节能力(即更大的曲率)。
但是，我们不希望每个像素都用同样的提亮函数。比如如果图像中某个地方亮着灯，那么这个地方的像素值就不用改变。因此，每个像素应该有独立的α
。最终的提亮函数为：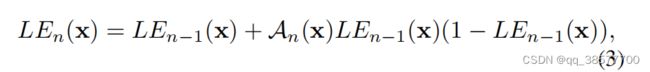
其中A是与给定图像具有相同大小的参数映射。这里，假设局部区域中的像素具有相同的强度(也是相同的调整曲线)，因此输出结果中的相邻像素仍然保持单调关系。这样，像素级高阶曲线也符合上述三个目标。结果，增强图像的每个像素值仍然在[0，1]的范围内。
下图显示了某输入图片在不同像素处的α的绝对值：

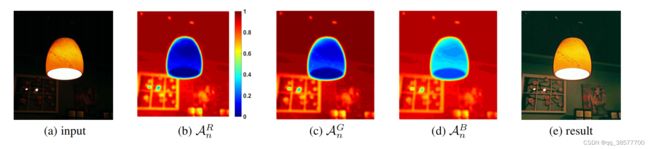
可以看出，在较亮的地方，图像没有变化，α几乎为0；而在较暗的地方，α的数值也较大。

3.2 DCE-Net

为了学习输入图像与其最佳拟合曲线参数图之间的映射关系，我们提出了一种深度曲线估计网络(DCE-Net)。在图4中，我们给出了DCE-NET的详细网络结构和参数设置。

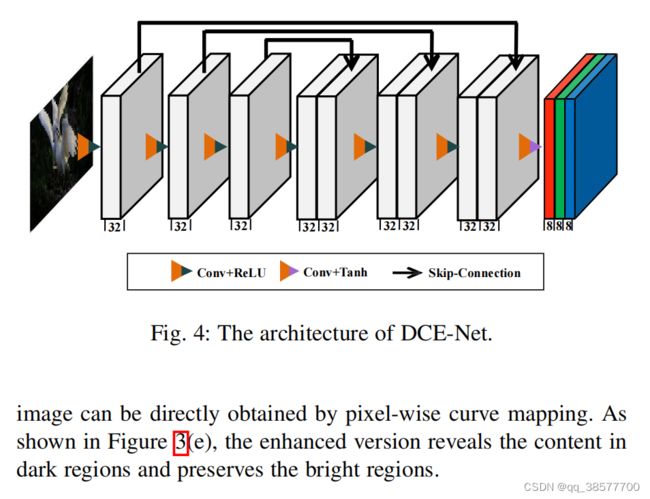
DCE-Net的输入是暗光图像，而输出是对应高阶曲线的一组像素级曲线参数图。我们不使用需要固定输入大小的全连通层，而是采用具有对称跳跃级联的七层卷积层的普通CNN。在前6个卷积层中，每个卷积层由32个大小为3×3、步长为1的卷积核组成，其后是RELU激活函数。最后一个卷积层由24个大小为3×3、步长为1的卷积核组成，其后是Tanh激活函数，该函数为8次迭代产生24个曲线参数图，其中每次迭代为3个通道(即，RGB通道)生成3个曲线参数图。我们去掉了打破相邻像素关系的下采样和批归一化层。值得注意的是，对于1200×900×3的输入图像，DCE-Net只有79K可训练参数和85G Flops，这已经小于现有的微光图像增强深度模型，如：RetinexNet：555k/587G，EnlighttenGan：8M/273G和MBLLEN：450k/301G。

3.3 无参考损失函数

为了在DCE网络中实现零参考学习，我们提出了一套可微分非参考损失，使我们能够评估
增强图像的质量。以下四种类型的损失是用于培训我们的DCE网:

3.3.1 空间一致性损失

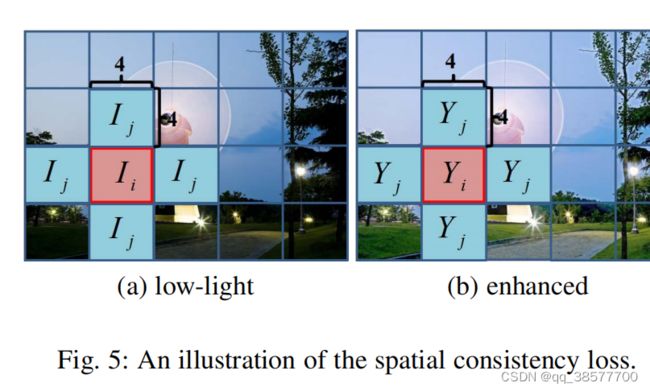
空间一致性损失Lspa通过保留输入图像与其增强版本之间的相邻区域的差异来鼓励增强图像的空间一致性：
其中K是局部区域的数目，Ω(I)是以区域i为中心的四个相邻区域(上、下、左、右)。我们将Y和I值分别表示为增强版和输入图像中局部区域的平均亮度值。我们经验地将局部区域的大小设置为4×4。考虑到其他区域大小，这种损失是稳定的。我们在图5中说明了计算空间一致性损失的过程。

3.3.2曝光控制损失

为了抑制曝光不足和过度曝光的区域，我们设计了曝光控制Lexp来控制曝光水平。曝光控制损失测量局部区域的平均强度值到良好曝光水平E之间的距离。我们遵循现有的实践来设置RGB颜色空间中的灰度级。在我们的实验中，我们经验性地将E设为0.6。损失Lexp可以表示为：

E设置成0.6表示充分暴露在光照下RGB颜色空间中的灰色级别，Y表示增强图像中局部区域的平均强度值，每个区域的大小为16X16

3.3.3 彩色恒常损失函数

是因为没有任何的监督信息的条件下，在RGB 3通道进行曲线映射的过程中会出现颜色偏差等问题。我们采用了一种先验的方式，利用灰度世界假设来限制RGB 3通道的关系。该假设条件是在增强的结果中，RGB 3通道的均值是无限的互相接近的。

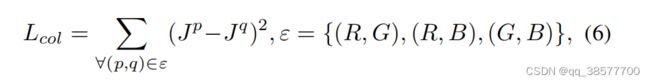
其中Jp表示增强图像中p通道的平均强度值，一对通道表示为(p,q)。

3.3.4 亮度平滑损失函数

当将高阶曲线扩展为逐像素的高阶曲线的时候，往往会破坏原始的曲线是单调的假设。为了避免这样问题的出现，我们将所估计的参数图进行平滑处理，使得相邻像素点的曲线参数值是相接近的，尽可能的保证曲线的单调性。

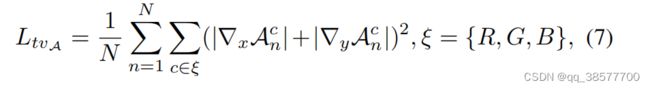
N：迭代次数 x,y表示水平和垂直梯度操作,A表示曲线参数图。

3.3.5 总损失

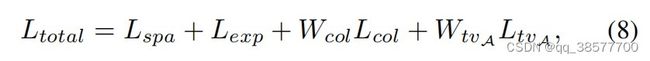
其中权重Wcol和WtvA用于平衡不同损失的作用。本文 Wcol= 0.5 ，WtvA = 20

4.ZERO-DCE++

在充分实验和观察的基础上，我们对Zero-DCE从三个方面进行优化，最终获得了参数更少，计算量更低，推理速度更快的Zero-DCE++。

采用轻量级的网络结构
在保持基本网络结构的基础上，我们采用深度可分离卷积替代传统的卷积层从而大幅降低网络的参数量和计算量。
简化亮度增强曲线
在经过大量试验后，我们发现在每次迭代过程中变化微小（如图所示），可以采取一个统一的曲线参数近似代替，因此我们将亮度增强曲线简化为：

A表示相同的增强曲线参数。这样不仅可以减少参数数量，还可以进一步提升模型的推理速度。
对输入图像进行下采样用于估计曲线参数
图像的像素之间存在大量的冗余信息，且网络估计的曲线参数图具有平滑的特性。基于以上原因，我们对输入图像进行下采样用于估计曲线参数，再将曲线参数上采样至原始尺寸后用于图像的迭代增强。

根据主观和客观测评结果，均衡算法性能和计算效率，在算法实施中我们选择12倍下采样。图5展示了一个场景在不同下采样倍率下的增强结果。

5.实验

5.1实验

基于CNN的模型通常使用自捕获的配对数据进行网络训练，而基于GAN的模型则精心选择未配对的数据。为了充分发挥宽动态范围调节的能力，我们将弱光和过曝光的图像都加入到我们的训练集中。为此，我们使用SICE数据集第1部分中的360个多次曝光序列来训练我们的模型。该数据集还用作EnlighttenGAN中训练数据的一部分。我们将第一部分子集中不同曝光级别的3022张图像随机分成两部分(2422张用于训练，其余用于验证)。我们将训练和测试图像的大小调整为512×512×3。
我们在NVIDIA 2080Ti图形处理器上实现了我们的框架。应用的批次大小为8。采用标准零均值和0.02标准差高斯函数对各层的滤波权重进行初始化。偏置被初始化为常量。我们使用带有默认参数和固定学习速率的ADAM优化器1e−4进行网络优化。权重WcolA和Wtva分别设置为0.5和20，以平衡损失规模。ZERO-DCE和ZERO-DCE++在训练期间采用相同的训练数据集和配置。