【视觉SLAM入门】6.1. (基于直接法的视觉里程计)LK光流法,代码解读, 直接法,特征点法对比,稀疏,半稠密,稠密地图
"刺卵掷地,逐蝇弃笔"
- 0. 数据集
- 1. 光流法(Optical Flow)
-
- 1.1. 光流
- 1.2. LK光流法
- 1.3 关键代码:
- 1.4 特点
- 2. 直接法(Direct Methods)
-
- 2.1 分类比较
- 2.2 优缺点
前置事项: 特征点耗时,丢弃有用信息,特征缺失(长直走廊)失效
对此,有直接法。
0. 数据集
该项目用的是fr1_desk数据集,RGBD的,下载后的全称是rgbd_dataset_freiburg1_desk.tgz。TUM官网数据集下载.
下载后,将rgb,depth文件夹和rgb.txt,depth.txt,groudtruth.txt拷贝到ch8的data/下(覆盖),然后执行脚本
python associate.py rgb.txt depth.txt > associate.txt
1. 光流法(Optical Flow)
1.1. 光流
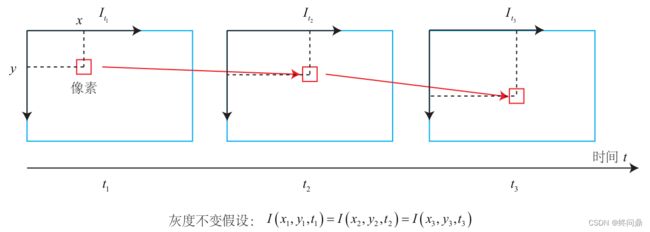
直接法前身:光流。上图中 I I I 表示灰度, t t t 表示时间
1.2. LK光流法
- 描述像素随着时间,在图像之间运动的方法。计算全部像素称为稠密光流,部分像素运动称为稀疏光流,稀疏光流代表作 Lucas-Kanade
- 仍用特征点,关键点不变,但是用光流取代描述子匹配的环节。
- 灰度不变假设:同一个空间点的像素灰度值,在各个图像中是固定不变的。
在该假设下,某像素运动到t时刻时灰度不变,则:
I ( x + d x , y + d y , t + d t ) = I ( x , y , t ) ⇓ 泰勒展开,保留一阶 I ( x + d x , y + d y , t + d t ) ≈ I ( x , y , t ) + ∂ I ∂ x d x + ∂ I ∂ y d y + ∂ I ∂ t d t ⇓ 由于灰度不变 ∂ I ∂ x d x + ∂ I ∂ y d y + ∂ I ∂ t d t = 0 ⇓ 两边除以 d t ∂ I ∂ x d x d t + ∂ I ∂ y d y d t = − ∂ I ∂ t I(x+dx, y+dy, t+dt) = I(x, y,t) \\\;\\\Downarrow 泰勒展开,保留一阶\\\;\\ I(x+dx, y+dy, t+dt) \approx I(x,y,t)+\frac{\partial I}{\partial x}dx + \frac{\partial I}{\partial y}dy + \frac{\partial I}{\partial t}dt \\\;\\\Downarrow 由于灰度不变\\\;\\ \frac{\partial I}{\partial x}dx + \frac{\partial I}{\partial y}dy + \frac{\partial I}{\partial t}dt=0 \\\;\\\Downarrow 两边除以dt\\\;\\ \frac{\partial I}{\partial x} \frac{dx}{dt} + \frac{\partial I}{\partial y}\frac{dy}{dt} = - \frac{\partial I}{\partial t} I(x+dx,y+dy,t+dt)=I(x,y,t)⇓泰勒展开,保留一阶I(x+dx,y+dy,t+dt)≈I(x,y,t)+∂x∂Idx+∂y∂Idy+∂t∂Idt⇓由于灰度不变∂x∂Idx+∂y∂Idy+∂t∂Idt=0⇓两边除以dt∂x∂Idtdx+∂y∂Idtdy=−∂t∂I
为了简化,做一些记法:
- 记 d x d t = u \frac{dx}{dt}=u dtdx=u(实则是像素在x轴上的运动速度),
- 记 d y d t = v \frac{dy}{dt}=v dtdy=v(实则是像素在y轴上的运动速度),
- 记 ∂ I ∂ x = I x \frac{\partial I}{\partial x}=I_x ∂x∂I=Ix(实则是图像在该点处x方向梯度),
- 记 ∂ I ∂ y = I y \frac{\partial I}{\partial y}=I_y ∂y∂I=Iy(实则是图像在该点处y方向梯度),
- 记 ∂ I ∂ t = I t \frac{\partial I}{\partial t}=I_t ∂t∂I=It(实则是图像灰度对时间的变化量)
求解如下矩阵:
[ I x I y ] [ u v ] = − I t \begin{bmatrix} I_x&I_y \end{bmatrix}\begin{bmatrix} u\\v \end{bmatrix} = -I_t [IxIy][uv]=−It
在LK光流中,为了求解u,v,需要引入更多约束,假设一个窗口内的像素具有相同运动,即多个点的 u , v u,v u,v 相同,则对于一个 w ⋅ w w\cdot w w⋅w的窗口,有 w 2 w^2 w2个 { I x , I y , I t } \{I_x,I_y,I_t\} {Ix,Iy,It}点对,则$有 w 2 w^2 w2 个方程可以用来求解 u , v u,v u,v。超定方程,求最小二乘解,即可得到 u , v u,v u,v。
得到了 u , v u,v u,v即图像运动速度后,当给定 t t t 时,就可以计算(估计)某块像素在若干个图像中出现的位置。
在SLAM中,LK光流常常被用来跟踪角点的运动。
1.3 关键代码:
cv::calcOpticalFlowPyrLK( last_color, color, prev_keypoints, next_keypoints, status, error );
OpenCV 库中的一个函数,用于计算光流(optical flow)。
函数的参数解释如下:
- last_color: \qquad\qquad\; 输入参数,表示上一帧的彩色图像。
- color: \qquad\qquad\qquad 输入参数,表示当前帧的彩色图像。
- prev_keypoints: \qquad\;\; 输入参数,表示上一帧的关键点(keypoints)位置。
- next_keypoints: \qquad\;\; 输出参数,表示当前帧的关键点位置。(主要)
- status: \qquad\qquad\qquad 输出参数,表示每个关键点的跟踪状态。如果跟踪成功,则状态为 true;否则为 false。跟踪失败的关键点后续可以删除
- error: \qquad\qquad\qquad 输出参数,表示每个关键点在运动模型下的估计误差。
该函数使用 Lucas-Kanade (LK) 方法计算光流。在给定上一帧的关键点位置和当前帧的图像,函数尝试在当前帧中估计新的关键点位置。函数返回每个关键点的跟踪状态和估计误差。如果跟踪成功,则 next_keypoints 中包含新的关键点位置;否则,这些位置是未定义的。
总的来说效果如下,抽取两张:
 \;\;\;\;\;\;\;\;\;\;
\;\;\;\;\;\;\;\;\;\; 
\qquad\qquad\qquad\qquad\quad t0时刻提取的关键点 \qquad\qquad\qquad\qquad\quad\qquad\qquad\qquad\qquad t0+t时刻提取的关键点
1.4 特点
- 匹配描述子方法相机运动较大时仍能成功,而光流法要求相机运动微小,鲁棒性差。
- 光流法不太会误匹配,只会跟丢特征点,优点。
2. 直接法(Direct Methods)
和光流有一定相似性,是基于优化的方法。
仍然基于灰度不变假设: 假设一个空间点在各个视角下,成像的灰度是不变的。
有一个初始位姿(必定不够好),和上一讲一样,但此时最小化的不是重投影误差,而是光度误差 (Photometric Error),也就是P的两个像的亮度误差:
e = I 1 ( p 1 ) − I 2 ( p 2 ) e = I_1(p_1)-I_2(p_2) e=I1(p1)−I2(p2)
其余的推导,李群李代数泰勒展开等同优化最小化重投影误差求解相机位姿那一节,最终仍使用G2O求解。
- G2O没有计算光度误差的边,我们需要自定义一种新的边。
2.1 分类比较
- 稀疏直接法: 选点来自稀疏关键点,如L-K光流一样,假设窗口灰度不变,只用数百个像素,不必计算描述子。速度最快,但只能计算稀疏的重构;
- 半稠密直接法(Semi-Dense): 选点只使用带有梯度的像素点,对计算运动增量没有贡献的点不用。可以重构一个半稠密结构。
- 稠密直接法: 计算所有像素(几十万~几百万个),多数需要GPU加速,但是梯度不明显的点,在运动估计中不会有太大贡献,重构时也难以估计其位置。
- 稀疏方法可以快速求解相机位姿,稠密方法可以建立完整地图,稀疏直接法可以做到非常快速的效果。
上述只分析了单个像素的差异,周围可能有很多像素和它的亮度差不多,所以我们有时候又使用小的图像块(patch),并且使用更复杂的度量方式,比如归一化相关性。(NCC)
2.2 优缺点
- 省时;
- 只要有像素梯度即可,无需特征点。图像有渐变,无特征点仍然可用。
- 可以构建半稠密地图和稠密地图。
缺点:
4. 非凸性----完全依靠梯度搜索;
5. 单个像素没有区分度;
6. 灰度不变性假设一般不成立:相机曝光等。