Leetcode dfs bfs相关题目(二)

Leetcode857雇佣k名工人的最低成本

这个题说工资支付是按照工作量成比例的，设Wa，Wb为实际支付的工资，设qa,qb为每个人的工作量，那么因该有 Wa:Wb = qa : qb
也就是这个组中的所有人的实际支付的工资:个人工作量是一个定值，并且题目中描述说，每个人至少会拿到自己的期望工资，也就是说
Wa/qa = x 而 Wa = x * qa >= Ea, 即 x >= Ea / qa 也就是说这个工资系数，至少是Ea/qa 也就是每个人的期望工资/每个人的工作量， 也就是这个k个工人组成的集合中，工资系数是最大的那个期望工资/工作量

然后，我们对每个人的 Ea/qa 进行从小到大排序，枚举这个工人的这个性价比作为k个工人组的工资系数x， 然后我们需要选择k-1个工资系数小于这个值的工人，满足实发工资最小即可，而实发工资 = 工资系数 * 劳动值， 也就是说求劳动值和最小即可

然后我们每次枚举一个新的工资系数的时候，把这个工人加进去，得把劳动量最多的那个工人给弹出来，这样用一个优先队列来维护即可

struct Person{
    int wage; //期望工资
    int work;  //工作量
    double ratio; //工资系数
}nodes[10010],heap[10010];
int cnt; //堆的大小

int cmp(const void* a,const void* b)
{
    struct Person* aa = (struct Person*)a;
    struct Person* bb = (struct Person*)b;
    if(aa->ratio > bb->ratio) return 1;
    return -1;
}

void down(int x)
{
    int tt = x;
    if(2*x <= cnt && heap[tt].work < heap[2*x].work) tt = 2 * x;
    if(2*x+1 <= cnt && heap[tt].work < heap[2*x+1].work) tt = 2*x+1;
    if(tt != x)
    {
        int temp_wage = heap[x].wage,temp_work = heap[x].work;
        double temp_ratio = heap[x].ratio;
        heap[x].work = heap[tt].work;
        heap[x].wage = heap[tt].wage;
        heap[x].ratio = heap[tt].ratio;
        heap[tt].wage = temp_wage;
        heap[tt].work = temp_work;
        heap[tt].ratio = temp_ratio;
        down(tt);
    }
}

double mincostToHireWorkers(int* quality, int qualitySize, int* wage, int wageSize, int k){
    int n = qualitySize;
    for(int i = 0; i < n; i++){
        nodes[i].wage = wage[i];
        nodes[i].work = quality[i];
        nodes[i].ratio = (double)wage[i] / (double)quality[i]; //整数转浮点除法一定要先把整数转浮点数后再运算
    }
    qsort(nodes,n,sizeof(nodes[0]),cmp);
    cnt = 0; //记录堆中元素个数
    for(int i = 0; i < k; i++){
        heap[++cnt] = nodes[i];
    }
    for(int i = cnt / 2; i; i--) down(i);
    double res  = 0;
    double work_sum = 0; //记录k个工人的总工作量
    double ratio = nodes[k-1].ratio; //这组中的工资系数
    for(int i = 1; i<= cnt; i++){
        printf("%d %d %lf\n",heap[i].wage,heap[i].work,heap[i].ratio);
        work_sum += heap[i].work;
    }
    res = work_sum * ratio;
    for(int i = k; i < n; i++){
        ratio = nodes[i].ratio; //枚举工资系数
        work_sum = work_sum - heap[1].work + nodes[i].work;
        res = fmin(res,work_sum*ratio);
        heap[1].wage = nodes[i].wage;
        heap[1].work = nodes[i].work;
        heap[1].ratio = nodes[i].ratio;
        for(int j = cnt / 2; j; j--) down(j);
    } 
    return res;
}

Leetcode爱吃香蕉的珂珂(二分)

int cmp(const void *a, const void* b)
{
    int* aa = (int*)a;
    int* bb = (int*)b;
    if(*aa < *bb) return 1;
    return -1;
}

bool check(int* nums,int n,int h,int k)
{
    long long hour = 0;
    for(int i = 0; i < n; i++){
        if(k == 0) return false;
        if(nums[i] % k == 0) hour = hour + nums[i] / k;  //如果正好整除就不用再加1了
        else hour = hour + nums[i] / k + 1;             //如果不是整除，得上取整
    }
    if(hour > h) return false;
    return true;
}

int minEatingSpeed(int* piles, int pilesSize, int h){
    int n = pilesSize;
    int l = 0, r = piles[0];
    for(int i = 0; i < n; i++) r = fmax(r,piles[i]);
    while(l < r){
        int mid = (l + r)/2;
        if(check(piles,n,h,mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

Leetcode1011在D天内送达包裹的能力

bool check(int* weights,int n,int D,int x) //检查船的承重为x的时候，能不能让货物在D天内全部装完
{
    int sum = 0; //每天装载的总重量
    int len = 1; //全部装载完毕需要的天数
    for(int i = 0; i < n; i++){
        if(weights[i] > x) return false;
        if(sum + weights[i] > x){
            len++;
            sum = 0;
        }
        sum += weights[i];
    }
    if(len <= D) return true;
    return false;
}

int shipWithinDays(int* weights, int n, int days){
    int sum = 0;
    for(int i = 0; i < n; i++) sum += weights[i];
    int l = 0, r = sum;
    while(l < r){
        int mid = (l + r)/2;
        if(check(weights,n,days,mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

Leetcode1723完成所有工作的最短时间

int cmp(const void* a,const void* b)
{
    int* aa = (int*)a;
    int* bb = (int*)b;
    if(*aa < *bb) return 1;
    return -1;
}

//k是工人分配时长数组的长度，u是当前已经分配到哪一个任务了,h是需要判断的时长
bool check(int* jobs,int n,int* worker,int k,int u,int h)
{
    if(u >= n) return true; //如果所有任务都能够被分配出去，那么h是合法的时间
    for(int i = 0; i < k; i++){
        if(worker[i] + jobs[u] <= h){
            worker[i] = worker[i] + jobs[u];
            if(check(jobs,n,worker,k,u+1,h)) return true;
            worker[i] -= jobs[u];
        }
    }
    return false;
}

int minimumTimeRequired(int* jobs, int n, int k){
    qsort(jobs,n,sizeof(jobs[0]),cmp);
    int sum = 0;
    for(int i = 0; i < n; i++) sum += jobs[i];
    int l = 0 ,r = sum;
    while(l < r)
    {
        int mid = (l + r)/2;
        int worker[k+1];
        memset(worker,0,sizeof(worker));
        if(check(jobs,n,worker,k,0,mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

Leetcode437 路径总和III

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
long long res;

long long dfs(struct TreeNode* root,int target) //dfs表示以root为根节点，值为target的路径条数
{
    if(!root) return 0;
    long long ans = 0;
    if(root->val == target) ans++;
    ans += dfs(root->left,target-root->val);
    ans += dfs(root->right,target-root->val);
    return ans; 
}

void dfs2(struct TreeNode* root,int target){ //枚举每个点作为根节点的情况
    if(!root) return;
    res += dfs(root,target);
    dfs2(root->left,target);
    dfs2(root->right,target);
}

int pathSum(struct TreeNode* root, int target){
    if(!root) return 0;
    res = 0;
    dfs2(root,target);
    return res;
}

Leetcode543 二叉树的直径

二叉树的直径仅仅看叶子节点到另一个叶子节点的最长的那条路径

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int res; 
int dfs(struct TreeNode* root){//返回从root走到叶子节点的最长的那条路径的节点数
    if(!root) return 0;
    int ans = 1;
    int left = dfs(root->left);
    int right = dfs(root->right);
    res = fmax(res,1+left+right);  //最大结果肯定是以某个点为根的一个路径，所以计算/\这种形式的路径长度即可
    return 1+fmax(left,right);
}

int diameterOfBinaryTree(struct TreeNode* root){
    res = 1;
    dfs(root);
    return res-1; //注意最终结果是路径数，比节点数小1
}

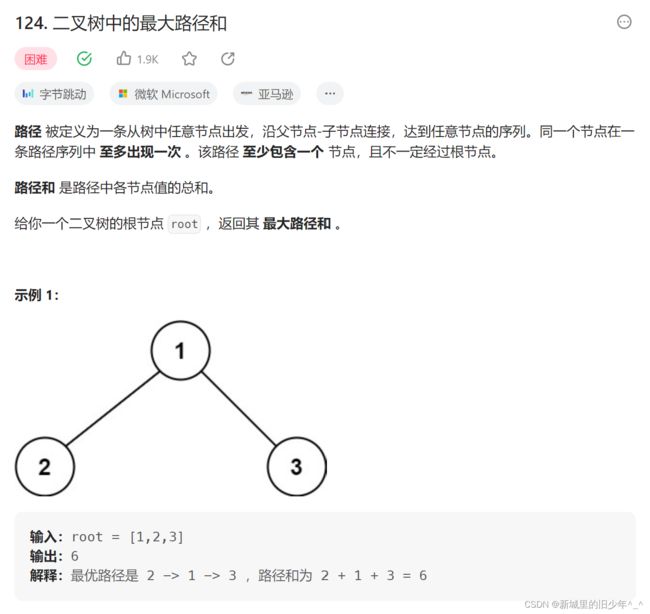
Leetcode124 二叉树最大路径和

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int res;
int dfs(struct TreeNode* root){
    if(!root) return 0;
    int left = fmax(0,dfs(root->left));
    int right = fmax(0,dfs(root->right));
    res = fmax(res,left+root->val+right);
    return root->val + fmax(left,right);
}

int maxPathSum(struct TreeNode* root){
    res = -0x3f3f3f3f;
    dfs(root);
    return res;
}

Leetcode 207课程表(拓扑排序)

#define N (int)(1e5+10)
int visit[N];  
int cnt; //判断已经拓扑排序访问了多少个点了
int degree[N]; //每个点的入度
int queue[N];
int front,tail;

int e[N],ne[N],h[N],idx;  //这题数据是1e5没法用g[N][N]，只能用邻接表来存储
void add(int a,int b){ //在图中已有的值a后面添加一个到b的边
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx++;
}

bool canFinish(int n, int** prerequisites, int prerequisitesSize, int* prerequisitesColSize){
    memset(visit,0,sizeof(visit));
    memset(h,-1,sizeof(h));
    memset(degree,0,sizeof(degree));
    idx = 0, cnt = 0;
    front = 0, tail = -1;
    for(int i = 0; i < prerequisitesSize; i++){
        int a = prerequisites[i][1];
        int b = prerequisites[i][0];
        add(a,b);
        degree[b]++;
    }
    //拓扑排序
    for(int i = 0; i < n; i++){
        if(degree[i] == 0) queue[++tail] = i; //入度为0的点入队
    }
    if(tail == -1) return false; //如果没有入度为0的点，肯定是错误的
    while(front <= tail){
        int node = queue[front++];
        cnt++;
        for(int i = h[node]; i != -1; i = ne[i]){
            int j = e[i];
            degree[j]--;
            if(degree[j] == 0) queue[++tail] = j;
        }
    }
    if(cnt != n) return false;
    return true;

}

模板题：Acwing848 有向图的拓扑序列

#include 
#include 
#include 
#define N (int)(1e5+10)
int e[N],ne[N],h[N],idx = 0;
int visit[N],degree[N]; //visit记录这个点是否被访问过，degree记录每个点的入度
int queue[N]; 
int front = 0, tail = -1;
int res[N],cnt = 0; //记录拓扑排序的结果
int n,m;

void add(int a,int b) //把b这个值添加到图中a这个节点的后面
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx++;
}

int main()
{
    scanf("%d%d",&n,&m);
    memset(degree,0,sizeof(degree));
    memset(visit,0,sizeof(visit));
    memset(h,-1,sizeof(h));
    while(m--){
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
        degree[b]++;
    }
    //拓扑排序
    for(int i = 1; i <= n; i++){
        if(degree[i] == 0) queue[++tail] = i; //把入度为0的点加入队列之中
    }
    if(tail < front){
        printf("-1\n");
        return 0;
    }
    while(front <= tail){
        int node = queue[front++];
        res[cnt++] = node;
        for(int i = h[node]; i != -1; i = ne[i]){
            int j = e[i];
            degree[j]--;
            if(degree[j] == 0) queue[++tail] = j;
        }
    }
    if(cnt != n){
        printf("-1\n");
        return 0;
    }
    for(int i  =0; i < cnt; i++) printf("%d ",res[i]);
    return 0;
}