Hands on RL 之 Deep Deterministic Policy Gradient（DDPG）

Hands on RL 之 Deep Deterministic Policy Gradient（DDPG）

1. 理论部分

1.1 回顾 Deterministic Policy Gradient(DPG)

在介绍DDPG之前，我们先回顾一下DPG中最重要的结论，

Deterministic Policy Gradient Theorem即确定性策略梯度定理

$$\begin{array}{rl}{\nabla }_{\theta }J({\mu }_{\theta })& ={\int }_{\mathcal{S}}{\rho }^{\mu }(s){\nabla }_{\theta }{\mu }_{\theta }(s){\nabla }_a{Q}^{\mu }(s,a){|}_{a={\mu }_{\theta }(s)}\mathrm{d}s\\ & ={\mathbb{E}}_{s\sim {\rho }^{\mu }}[{\nabla }_{\theta }{\mu }_{\theta }(s){\nabla }_a{Q}^{\mu }(s,a){|}_{a={\mu }_{\theta }(s)}]\end{array}$$

其中，$a={\mu }_{\theta }(s)$表示确定性的策略是从状态空间到动作空间的映射${\mu }_{\theta }:\mathcal{S}\to \mathcal{A}$，网络的参数为$\theta$，$s\sim {\rho }^{\mu }$表示状态$s$符合在策略$\mu$下的状态访问分布。如何推导的，这里不详细阐述。（可以参考Deterministic policy gradient algorithms）

接下来逐点介绍DDPG相较于DPG的改进

1.2 Neural Network Difference

​ DDPG在相较于传统的AC算法在网络结构上也有很大不同，首先看看传统算法的网络结构

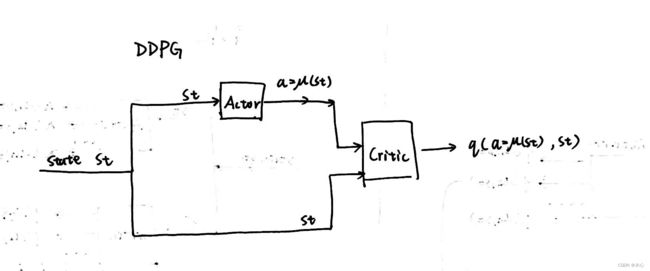
然后再看看DDPG的网络结构

为什么DDPG会是这样的网络结构呢，这是因为DDPG中的actor输出的是确定性动作，而不是动作的概率分布，因此确定性的动作是连续的可以看作动作空间的维度为无穷，如果采用AC中critic的结构，我们无法通过遍历所有动作来取出某个特定动作对应的Q-value。因此DDPG中将actor的输出作为critic的输入，再联合状态输入，就能直接获得所采取动作$a=\mu (st)$的Q-value。

1.3 Why is off-policy?

​ 首先为什么DDPG或者说DPG是off-policy的？我们回顾stochastic policy ${\pi }_{\theta }(a|s)$定义下的Q-value
$$Q^{\pi }(s_t,a_t)={\mathbb{E}}_{r_t,s_{t+1}\sim E}[r(s_t,a_t)+\gamma {\mathbb{E}}_{a_{t+1}\sim \pi }[Q^{\pi }(s_{t+1},a_{t+1})]]$$
其中，$E$表示的是环境，即状态$s\sim E$状态符合环境本身的分布。当我们使用确定性策略的时候$a={\mu }_{\theta }(s)$，那么inner expectation就自动被抵消掉了
$$Q^{\pi }(s_t,a_t)={\mathbb{E}}_{r_t,s_{t+1}\sim E}[r(s_t,a_t)+\gamma Q^{\pi }(s_{t+1},a_{t+1}=\mu (s_{t+1}))]$$
这就意味着Q-value不再依赖于动作的访问分布，即没有了$a_{t+1}\sim \pi$。那么我们就可以通过行为策略behavior policy $\beta$产生的结果来计算该值，这让off-policy成为可能。

​ 实际上Q-value不再依赖于动作的访问分布，那么确定性梯度定理可以写作
$${\nabla }_{\theta }J({\mu }_{\theta })\approx {\mathbb{E}}_{s\sim {\rho }^{\beta }}[{\nabla }_{\theta }{\mu }_{\theta }(s){\nabla }_a{Q}^{\mu }(s,a){|}_{a={\mu }_{\theta }(s)}]$$
可以写作依赖于behavior policy $\beta$产生的状态访问分布的期望，这就是一种off-policy的形式。

1.4 Soft target update

​ 在DDPG中维护了四个神经网络，分别是policy network, target policy network, action value network, target action value network。使用了DQN中的将目标网络和训练网络分离的思想，并且采用soft更新的方式，能够更有效维护训练中的稳定性。soft更新方式如下
$${\theta }^{-}\leftarrow \tau \theta +(1-\tau ){\theta }^{-}$$
其中，${\theta }^{-}$表示目标网络参数，$\theta$表示训练网络参数，$\tau \ll 1$，$\tau$是软更新参数。

1.5 Maintain Exploration

​ 确定性的策略是不具有探索性的，为了保持策略的探索性，我们可以在策略网络的输出中增加高斯噪声，让输出的动作值有些许偏差来增加网络的探索性。用数学的方式来表示即是
$${\mu }^{\prime }(s_t)={\mu }_{\theta }(s_t)+\mathcal{N}$$
其中${\mu }^{\prime }$表示探索性的策略，$\mathcal{N}$表示高斯噪声。

1.6 Other Techniques

​ DDPG还集成了一些别的算法的常用技巧，比如Replay Buffer来产生independent and identically distribution的样本，使用了Batch Normalization来预处理数据。

1.7 Pesudocode

伪代码如下

2. 代码实践

我们采用gym中的Pendulum-v1作为本次实验的环境，Pendulum-v1是典型的确定性连续动作空间环境，整体的代码如下

import torch
import torch.nn as nn
import torch.nn.functional as F
import gym
import random
from tqdm import tqdm
import numpy as np
import matplotlib.pyplot as plt
import collections

# Policy Network
class PolicyNet(nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim, action_bound):
        super(PolicyNet, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, action_dim)
        self.action_bound = action_bound
    
    def forward(self, observation):
        x = F.relu(self.fc1(observation))
        x = F.tanh(self.fc2(x))
        return x * self.action_bound

# Q Value Network
class QValueNet(nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(QValueNet, self).__init__()
        self.fc1 = nn.Linear(state_dim + action_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc_out = nn.Linear(hidden_dim, 1)
    
    def forward(self, x, a):
        cat = torch.cat([x, a], dim=1)    # 拼接状态和动作
        x = F.relu(self.fc1(cat))
        x = F.relu(self.fc2(x))
        return self.fc_out(x)

# Deep Deterministic Policy Gradient
class DDPG():
    def __init__(self, state_dim, hidden_dim, action_dim, 
                action_bound, actor_lr, critic_lr, 
                sigma, tau, gamma, device):
        self.actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
        self.critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
        self.target_actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
        self.target_critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)

        # initialize target actor network with same parameters
        self.target_actor.load_state_dict(self.actor.state_dict())
        # initialize target critic network with same parameters
        self.target_critic.load_state_dict(self.critic.state_dict())

        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
        self.gamma = gamma
        self.sigma = sigma  # 高斯噪声的标准差,均值直接设置为0
        self.action_dim = action_dim
        self.device = device
        self.tau = tau
    
    def take_action(self, state):
        state = torch.tensor(np.array([state]), dtype=torch.float).to(self.device)
        action = self.actor(state).item()
        # add noise to increase exploratory
        action = action + self.sigma * np.random.randn(self.action_dim)
        return action
    
    def soft_update(self, net, target_net):
        # implement soft update rule
        for param_target, param in zip(target_net.parameters(), net.parameters()):
            param_target.data.copy_(param_target.data * (1.0-self.tau) + param.data * self.tau)
    
    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
        rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1,1).to(self.device)
        actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1,1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1,1).to(self.device)

        next_q_values = self.target_critic(next_states, self.target_actor(next_states))
        td_targets = rewards + self.gamma * next_q_values * (1-dones)
        critic_loss = torch.mean(F.mse_loss(self.critic(states, actions), td_targets))

        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_optimizer.step()

        actor_loss = torch.mean( - self.critic(states, self.actor(states)))
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()

        # soft update actor net and critic net
        self.soft_update(self.actor, self.target_actor)
        self.soft_update(self.critic, self.target_critic)
    

class ReplayBuffer():
    def __init__(self, capacity):
        self.buffer = collections.deque(maxlen=capacity)
    
    def add(self, s, a, r, s_, d):
        self.buffer.append((s,a,r,s_,d))
    
    def sample(self, batch_size):
        transitions = random.sample(self.buffer, batch_size)
        states, actions, rewards, next_states, dones = zip(*transitions)
        return np.array(states), actions, np.array(rewards), np.array(next_states), dones

    def size(self):
        return len(self.buffer)


def train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size, render, seed_number):
    return_list = []
    for i in range(10):
        with tqdm(total=int(num_episodes/10), desc='Iteration %d'%(i+1)) as pbar:
            for i_episode in range(int(num_episodes/10)):
                observation, _ = env.reset(seed=seed_number)
                done = False
                episode_return = 0

                while not done:
                    if render:
                        env.render()
                    action = agent.take_action(observation)
                    observation_, reward, terminated, truncated, _ = env.step(action)
                    done = terminated or truncated
                    replay_buffer.add(observation, action, reward, observation_, done)
                    # swap states
                    observation = observation_
                    episode_return += reward
                    if replay_buffer.size() > minimal_size:
                        b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
                        transition_dict = {
                            'states': b_s,
                            'actions': b_a,
                            'rewards': b_r,
                            'next_states': b_ns,
                            'dones': b_d
                        }
                        agent.update(transition_dict)
                return_list.append(episode_return)
                if(i_episode+1) % 10 == 0:
                    pbar.set_postfix({
                        'episode': '%d'%(num_episodes/10 * i + i_episode + 1),
                        'return': "%.3f"%(np.mean(return_list[-10:]))
                    })
                pbar.update(1)
    env.close()
    return return_list

def moving_average(a, window_size):
    cumulative_sum = np.cumsum(np.insert(a, 0, 0)) 
    middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
    r = np.arange(1, window_size-1, 2)
    begin = np.cumsum(a[:window_size-1])[::2] / r
    end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
    return np.concatenate((begin, middle, end))

def plot_curve(return_list, mv_return, algorithm_name, env_name):
    episodes_list = list(range(len(return_list)))
    plt.plot(episodes_list, return_list, c='gray', alpha=0.6)
    plt.plot(episodes_list, mv_return)
    plt.xlabel('Episodes')
    plt.ylabel('Returns')
    plt.title('{} on {}'.format(algorithm_name, env_name))
    plt.show()



if __name__ == "__main__":
    # reproducible
    seed_number = 0
    random.seed(seed_number)
    np.random.seed(seed_number)
    torch.manual_seed(seed_number)

    num_episodes = 250     # episodes length
    hidden_dim = 128        # hidden layers dimension
    gamma = 0.98            # discounted rate
    actor_lr = 1e-3         # lr of actor
    critic_lr = 1e-3        # lr of critic
    tau = 0.005             # soft update parameter
    sigma = 0.01            # std variance of guassian noise
    buffer_size = 10000
    minimal_size = 1000
    batch_size = 64

    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    env_name = 'Pendulum-v1'

    render = False
    if render:
        env = gym.make(id=env_name, render_mode='human')
    else:
        env = gym.make(id=env_name)
                    
    state_dim = env.observation_space.shape[0]
    action_dim = env.action_space.shape[0]  
    action_bound = env.action_space.high[0]


    replay_buffer = ReplayBuffer(buffer_size)        
    agent = DDPG(state_dim, hidden_dim, action_dim, action_bound, actor_lr, critic_lr, sigma, tau, gamma, device)
    return_list = train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size, render, seed_number)

    mv_return = moving_average(return_list, 9)
    plot_curve(return_list, mv_return, 'DDPG', env_name)

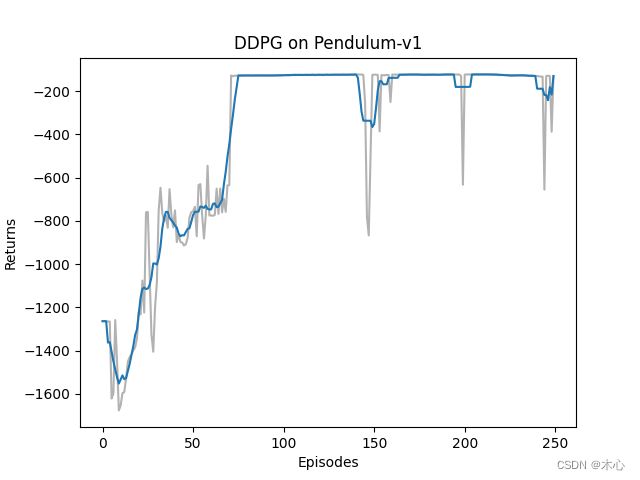
DDPG训练的回报曲线如图所示

Reference

Tutorial: Hands on RL

Paper: Continuous control with deep reinforcement learning