前缀和的综合应用(力扣C++题解)
目录
前缀和的作用:
构造前缀和的模板:
1:寻找数组的中心下标(简单)
2:逐步求和得到正数的最小值(简单)
3:找到最高海拔(简单)
4:所有奇数长度子数组的和(有点不简单)
5:检查是否区域内的所有整数都被覆盖(差分+前缀和)
6:长度最小的子数组(滑动窗口)
7:除自身以外数组的乘积
8:前缀和二维数组的应用
9:连续的子数组和(数学:同余定理+哈希)
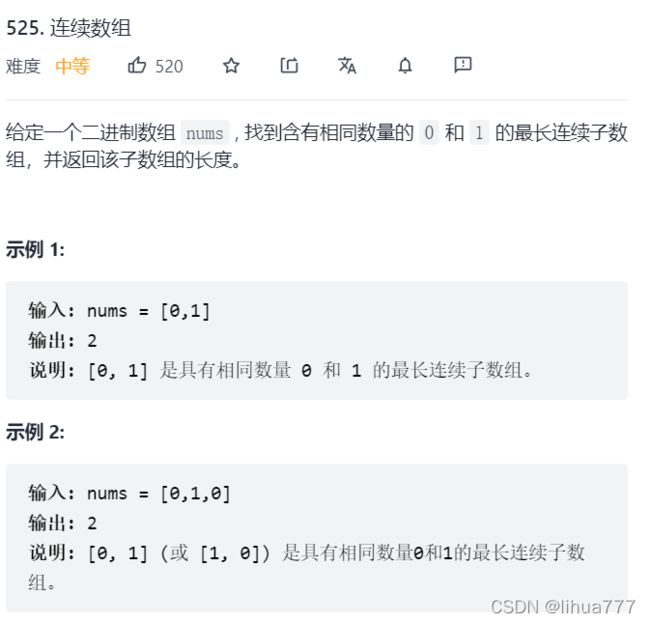
10:连续数组(前缀和+哈希)
11:和为K的子数组(前缀和+哈希)
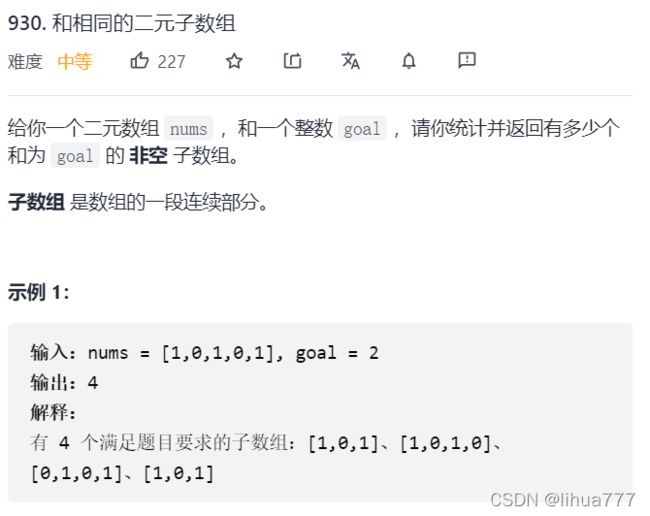
12:和相同的二元子数组(前缀和哈希+滑动窗口)
13:和可被K整除的子数组(前缀和+哈希)
13:最大连续1的个数|||(前缀和+滑动窗口)
前缀和的作用:
能求出一段区间内的数的和(在O(1)的时间内)
如果构造的sum是(n大小且sum[0]=nums[i]) ans=sum[right]-sum[left-1]
如果构造的sum是(n大小且sum[1]=nums[0]) ans=sum[right+1]-sum[left]
构造前缀和的模板:
n+1的模板:
class Solution {
public:
vector runningSum(vector& nums) {
int n=nums.size();
vector ans(n+1,0);
for(int i=0;i n的模板:
class Solution {
public:
vector runningSum(vector& nums) {
int n=nums.size();
vector ans(n+1,0);
for(int i=0;i 1:寻找数组的中心下标(简单)
思路解析:
中心下标:这个位置的左边的数之和==这个位置的右边的数之和
那么数组的总和为sum,就有组合公式leftsum+nums[i]+rightsum=sum
移项则有:leftsum=sum-rightsum-nums[i]
即我们只需求出sum,再遍历左侧前缀和即可
class Solution {
public:
int pivotIndex(vector& nums) {
int sum = 0;
for (int num : nums) sum += num; // 求和
int leftSum = 0; // 中心索引左半和
int rightSum = 0; // 中心索引右半和
for (int i = 0; i < nums.size(); i++) {
leftSum += nums[i];
rightSum = sum - leftSum + nums[i];
if (leftSum == rightSum) return i;
}
return -1;
}
}; 2:逐步求和得到正数的最小值(简单)
思路解析:
利用前缀和求出这个原数组nums对应的前缀和数组ans,题目要求的题意即可转变为将前缀和数组的最小值至少加上x,使得数组的每个数都大于或等于1
构造好前缀和数组后,我们初始化min=INT_MAX,求最小值,共有两种情况
如果min的值出来后大于等于1,那么证明前缀和数组都是正数,所以无需加上数字
如果min的值出来后小于1,那么就根据样例进行调整即可
class Solution {
public:
int minStartValue(vector& nums) {
int Min=INT_MAX;
int sum=0;
for(int num:nums)
{
sum+=num;
Min=min(Min,sum);
}
if(Min>=1) return 1;//证明数组中的数都是正数
else return abs(Min)+1;//数组中存在负数
}
}; 3:找到最高海拔(简单)
思路解析:
根据原数组构造出前缀和数组,并求出前缀和数组的最大值即可
class Solution {
public:
int largestAltitude(vector& gain) {
int n=gain.size();
vector ans(n+1,0);
for(int i=0;iMAX)
{
MAX=ans[i];
}
}
return MAX;
}
}; 4:所有奇数长度子数组的和(有点不简单)
思路解析:
有两条路的遍历方式:
(1)像解释一样,先遍历1个1组的,再遍历3个1组的,再遍历5个一组的…………
(2)先遍历以1为头的所有奇数数组,比如1本身和[1,4,2]和[1,4,2,5,3],再遍历以2为头的
这里选择第一种遍历方式
(1)构造前缀和
(2)步长限制(step)(当步长大于等于这个数组长度时,跳出)
(3)for循环用i遍历,把nums[i]作为每个的头,并以步长的单位进行求区间和
(4)更新步长:step+=2;
class Solution {
public:
int sumOddLengthSubarrays(vector& arr) {
int n=arr.size();
vector ans(n+1,0);
for(int i=0;i 5:检查是否区域内的所有整数都被覆盖(差分+前缀和)
思路解析:
vec数组:前缀和数组(初始化为0)
(1)差分构造:
在二维数组中,每一个元素也是一个区间,ranges[i][0]是左端点,ranges[i][1]是右端点:进行两次操作:<1>将左端点+1,<2>将右端点的右一个位置+1(差分性质等会会用到)
(2)在for循环里执行(1)操作,那么可以想象出vec数组的模样了,即数组的索引为端点的值,索引为左端点的值为1,索引为右端点的右一个方向为-1,其余的点的值均为0
(3)在for循环中构造出前缀和数组vec,由于前缀和的性质,那么我们可以知道,左端点为起点,右端点为终点,在前缀和数组是为非负的(有可能区间里还有一个区间)
如果这段区间为非负数,那么我们即可退出这段区间已经完全被覆盖 return true
相反:如果这段区间内有数字为负数,那么为不完全覆盖,return false
class Solution {
public:
bool isCovered(vector>& ranges, int left, int right) {
vector vec(52,0);
int n = ranges.size();
for(int i=0;i 6:长度最小的子数组(滑动窗口)
思路解析:
暴力:以j为终点,i为起点,寻找大于等于target的长度的子数组,并用res进行更新操作,时间复杂度明显为O(N^2)
int res=INT_MAX;
int sum=0;
for(int i=0;i=target)
res=min(res,j-i+1); 滑动窗口:
以right为终点,以left为起点,遍历right,并让sum+=nums[right],如果sum>=target,那么让left++,即缩短窗口,看看符合条件与否
时间复杂度为O(N):快指针和慢指针最多移动数组长度次
class Solution {
public:
int minSubArrayLen(int target, vector& nums) {
if(nums.empty()) return 0;
int left=0;
int sum=0;
int res=INT_MAX;
for(int right=0;right=target)
{
res=min(res,right-left+1);
sum-=nums[left];
left++;
}
}
return res==INT_MAX?0:res;
}
}; 7:除自身以外数组的乘积
思路解析:
相当于把前缀和变成了前缀乘,后缀和变成了后缀乘,且除自身外的乘积,相当于这个自身的左边乘积乘以右边的乘积(越界情况视为1)
class Solution {
public:
vector productExceptSelf(vector& nums) {
int n=nums.size();
vector ans(n,1);
int pre=1;
int suff=1;
//除自身以外数组的乘积==左侧的累乘乘积*右侧的累乘乘积
for(int i=0;i 8:前缀和二维数组的应用
另外一种方法在另一篇已写
本次写的是将二维数组转变为多个一维数组的写法
class NumMatrix {
public:
vector> sums;
NumMatrix(vector>& matrix)
{
int m = matrix.size();
if (m > 0) {
int n = matrix[0].size();
sums.resize(m, vector(n + 1));
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sums[i][j + 1] = sums[i][j] + matrix[i][j];
}
}
}
}
int sumRegion(int row1, int col1, int row2, int col2)
{
int sum = 0;
for (int i = row1; i <= row2; i++) {
sum += sums[i][col2 + 1] - sums[i][col1];
}
return sum;
}
}; 9:连续的子数组和(数学:同余定理+哈希)
思路解析:
同余定理:如果说有前缀和数组中一个元素它的余数为x,将这个位置标记为开始位置,向后寻找,如果数组中有一个元素它的余数也为x,将这个位置标记为结束位置,那么这个[开始位置,结束位置]区间内的子数组的和为K的倍数
原理:因为它是前缀和数组,那么被我们标记为开始位置的余数为x,且被我们标记为结束位置的余数为x,它们的余数相同,那么我们就可推断出,是开始位置之前的为子数组和%K=x,那么[开始区间,结束区间]这段区间内,相当余数为0,只有这样余数为2,才可能从开始位置保留到结束位置
对于查询余数和对应下标,这个是必须的操作,所以我们需要用到哈希表
key:余数(rem) val:位置
(1)求出前缀和的余数,<1>如果哈希表中存在这个数,那么存储这个数的当前位置,并让这个位置与之前余数相同的位置相减,如果位置差为>=2(题目要求子数组的大小至少为2),那么即可证明存在
<2>如果哈希表中不存在这个数,那么将这个余数作为索引,数的位置当作值,存储在哈希表中
class Solution {
public:
bool checkSubarraySum(vector& nums, int k) {
unordered_map map = { {0,-1} };
int rem = 0;
for (int i = 0; i < nums.size(); i++)
{
rem = (rem + nums[i]) % k;//C++特性:余数可为负数,这个操作是让它的余数为正数
if (map.count(rem))//
{
int pos = map[rem];
if (i - pos >= 2)
{
return true;
}
}
else
{
map[rem] = i;
}
}
return false;
}
}; 10:连续数组(前缀和+哈希)
思路解析:
难点在于:很明显的滑动窗口题却用不了滑动窗口,因为非有序,等等无法说得出口的语言
内心想法:1和0,构成前缀和,如果它们个数一样,也没什么特征,不就是几个1吗,能有什么特征,我要找的是最长连续数组,而且就算前缀和等于一个正整数,我也没法判断它是否是题目要求的,内心逐渐崩溃…………
突发奇想:如果我把数组中的0都换为-1,那么如果它们个数一样,那肯定是有特征的:即前缀和为0,如果不相等那么一定不为0!找到了特征,我们就要寻找这个子数组的开始位置和结束位置,特征为:开始位置的前缀和为x,结束位置的前缀和为x,与同余定理一个原理,因为只有满足这个条件,这个区间内的和才为0,1和-1的数量才相等
哈希表的原理与上同 key:前缀和的值 val:对应前缀和的下标
易懂版:
int findMaxLength(vector& nums)
{
size_t n = nums.size();
vector preSum(n + 1);
unordered_map mp;
mp[0] = -1;
size_t maxLen = 0;
for (size_t i = 0; i < n; ++i)
{
if (nums[i] == 0) nums[i] = -1;
preSum[i + 1] = preSum[i] + nums[i];
// 首次出现保存到unordered_map中
if (mp.find(preSum[i + 1]) == mp.end())
mp[preSum[i + 1]] = i;
// 在mp的就是preSum值之前首次出现的下标,更新最大值
else maxLen = max(maxLen, i - mp[preSum[i + 1]]);
}
return maxLen;
}
精简版:
class Solution {
public:
int findMaxLength(vector& nums) {
unordered_map m = {{0,-1}};
int cur = 0, ans = 0;
for(int i = 0; i < nums.size(); ++i)
{
nums[i] == 0? --cur : ++cur;
if(m.count(cur))
ans = max(ans, i - m[cur]);
else
m[cur] = i;
}
return ans;
}
};
细枝末节:
为什么要在哈希表中插入{0, -1},我觉得是这样的,快速计算子数组的和,j到i,所以
sum(i)-sum(j-1)。当计算的子数组仅为第一个元素时,下标是相等的i==j==0,套用公式
sum(0)-sum(0-1),这时,我们就会发现,我们需要一个下标为-1的前缀和。由于map的键为前缀和,
值为下标。下标我们有了,就是-1,但是它的前缀和是多少呢。由于前缀和就是前面的数字加前来的和,前面没有数字,所以键为0,得{0,-1}
11:和为K的子数组(前缀和+哈希)
难点:又是看起来可以用滑动窗口,但是用不了的寂寞,因为避免不了[1] k=0这种情况
暴力枚举:
class Solution {
public:
int subarraySum(vector& nums, int k)
{
int count = 0;
for (int start = 0; start < nums.size(); ++start)
{
int sum = 0;
for (int end = start; end >= 0; --end)
{
sum += nums[end];
if (sum == k)
{
count++;
}
}
}
return count;
}
}; 前缀和+哈希:哈希:key:值 val:频数
class Solution {
public:
int subarraySum(vector& nums, int k)
{
unordered_map mp;
mp[0] = 1;//特殊
int count = 0, pre = 0;
for (auto& x:nums) {
pre += x;
if (mp.find(pre - k) != mp.end())
{
count += mp[pre - k];
}
mp[pre]++;//每遍历到一个数,该数的次数+1
}
return count;
}
}; 细枝末节:mp[0]=1 -》》可以认为left会在nums[-1](当然这个是虚构出来便于理解的),right和left之间夹的是从nums[0]到当前的位置的子序列,且和为k。 那么初始化就相当于,在遍历数组前记录一下这个虚构的节点,它的值不计入sum,所以是0
人话就是:不初始化的话,数组中有重复元素和[-3,3] k=0 这种情况会出错
12:和相同的二元子数组(前缀和哈希+滑动窗口)
思路解析:前缀和+哈希(哈希:key:值 val:频数)与上题一模一样
class Solution {
public:
int numSubarraysWithSum(vector& nums, int goal) {
int n = nums.size();
unordered_map umap;
umap[0] = 1;//标记
int sum = 0;
int ans = 0;
for(int i=0;i 滑动窗口:
(因为数组中要么是0要么是1,所以我们用三指针,right是终点指针,left1是刚好满足指针,left2是极限满足指针)(left1和left2之间有0的情况)返回即返回ret=left2-left1即可
class Solution {
public:
int numSubarraysWithSum(vector& nums, int k) {
int n = nums.size();
int left1 = 0;
int left2 = 0;
int right = 0;
int ret = 0;
int sum1 = 0, sum2 = 0;
while (right < n)
{
sum1 += nums[right];
while (left1 <= right && sum1 > k)//求出刚好符合边界
{
sum1 -= nums[left1];
left1++;
}
sum2 += nums[right];
while (left2 <= right && sum2 >= k)//求出的是极限位置
{
sum2 -= nums[left2];
left2++;
}
ret += left2 - left1;
right++;
}
return ret;
}
}; 13:和可被K整除的子数组(前缀和+哈希)
思路解析:
(1)同余定理的应用
(2)哈希表:key:余数 val:频数
class Solution {
public:
int subarraysDivByK(vector& nums, int k) {
unordered_map record = { {0,1} };
int sum = 0;
int ans = 0;
for (int elem : nums)
{
sum += elem;
int modulus = (sum % k + k) % k;//取余的绝对值
if (record.count(modulus))
{
ans += record[modulus];//频数
}
record[modulus]++;//将前缀和的余数存储,并记录频数
}
return ans;
}
}; 13:最大连续1的个数|||(前缀和+滑动窗口)
思路解析:
模拟思想:子数组中只容许有K个0,那么滑动窗口,如果right遇到0,将增加0的个数,如果left遇到就减少0的个数那么此时,用res记录距离即可
class Solution {
public:
int longestOnes(vector& A, int K) {
int res = 0, zeros = 0, left = 0;
for (int right = 0; right < A.size(); ++right)
{
if (A[right] == 0) ++zeros;
while (zeros > K) //如果0的个数大于K的话
{
if (A[left++] == 0) --zeros;//用left进行补救,
}
res = max(res, right - left + 1);
}
return res;
}
};