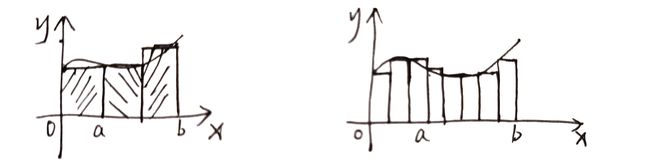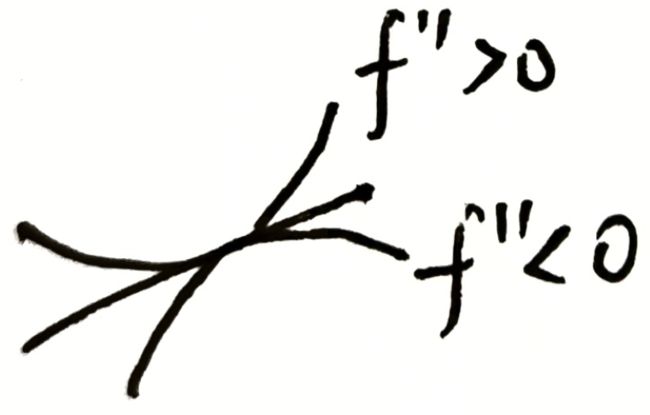【AI】数学基础——高数(积分部分)
高数(函数&微分部分)
文章目录
-
- 1.4 微积分
-
- 1.4.1 基本思想
- 1.4.2 定积分
-
- 定义
- 定义计算定积分
- 定积分性质
- 定理
- N-L公式
- 泰勒公式
- 麦克劳林公式
- 1.5 求极值
-
- 1.5.1 无条件极值
- 1.5.2 条件极值
- 1.5.3 多条件极值
- 1.5.4 凹函数与凸函数
1.4 微积分
用于求解速度、面积、体积等可累积量
1.4.1 基本思想
以直代曲
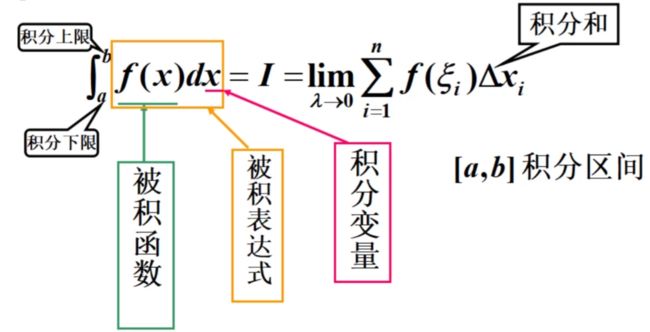
在 [ a , b ] [a,b] [a,b] 间插入若干点,得到 n n n 个小区间,每个小矩形面积 A i = f ( ξ i ) Δ x i ⇒ A ( a , b ) = ∑ i = 1 n f ( ξ i ) Δ x i A_i=f(\xi_i)\Delta x_i\Rightarrow A_{(a,b)}=\sum_{i=1}^n f(\xi_i)\Delta x_i Ai=f(ξi)Δxi⇒A(a,b)=∑i=1nf(ξi)Δxi
设 λ \lambda λ 为小区间的最大值, A = lim λ → 0 ∑ i = 1 n f ( ξ i ) Δ x i A=\lim_{\lambda\rightarrow 0}\sum_{i=1}^n f(\xi_i)\Delta x_i A=limλ→0∑i=1nf(ξi)Δxi
记为 ∫ a b f ( x ) d x \int_{a}^b f(x)dx ∫abf(x)dx
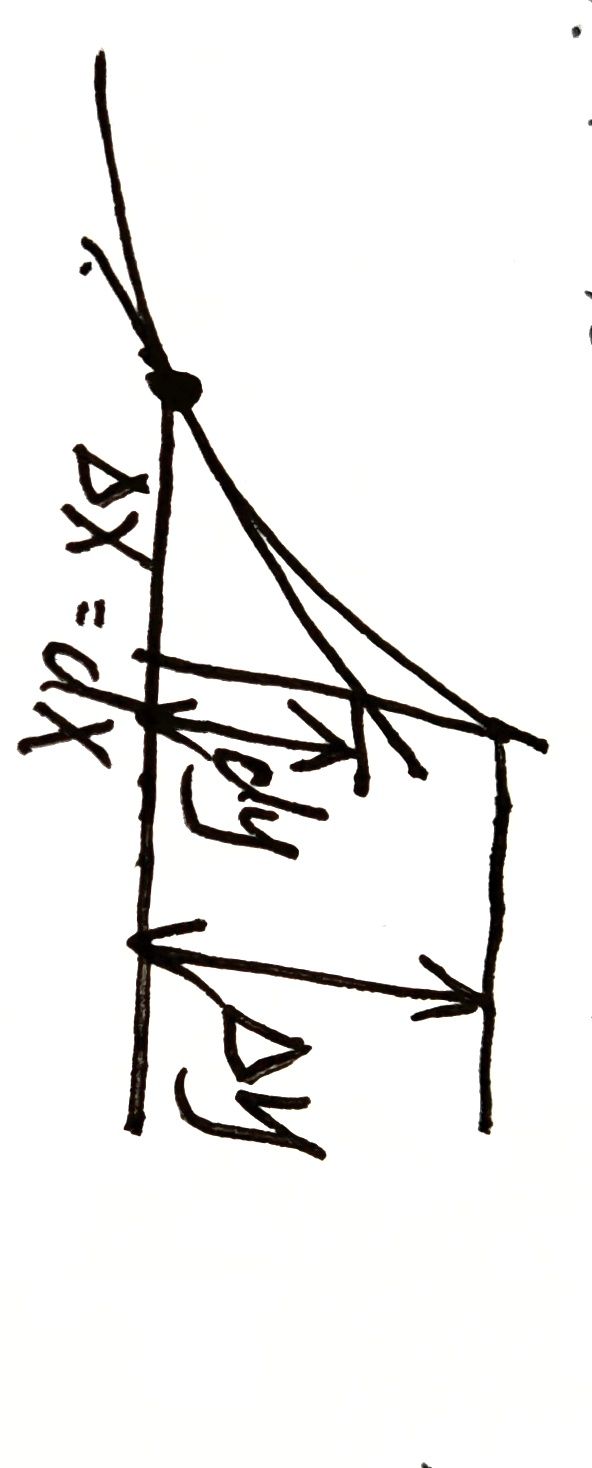
微分与导数关系
d y dy dy :切线增量
Δ y \Delta y Δy :曲线增量
导数(切线斜率): f ′ ( x ) = d y d x f'(x)=\frac{dy}{dx} f′(x)=dxdy
Δ y = d y + o ( Δ x ) \Delta y=dy+o(\Delta x) Δy=dy+o(Δx)
1.4.2 定积分
定义
函数可积定义: f ( x ) f(x) f(x) 在 [ a , b ] [a,b] [a,b] 上的定积分存在时,则称 f ( x ) f(x) f(x) 在 [ a , b ] [a,b] [a,b] 可积
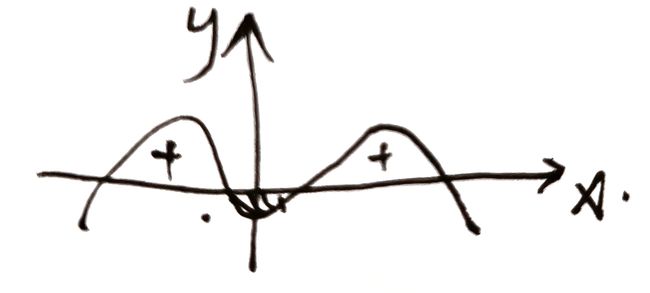
几何意义:面积A
{ f ( x ) > 0 ∫ a b f ( x ) d x = A > 0 f ( x ) < 0 ∫ a b f ( x ) d x = − A < 0 \left\{ \begin{aligned} &f(x)>0&\int_{a}^bf(x)dx=A>0\\ &f(x)<0&\int_{a}^bf(x)dx=-A<0 \end{aligned} \right. ⎩ ⎨ ⎧f(x)>0f(x)<0∫abf(x)dx=A>0∫abf(x)dx=−A<0
定义计算定积分
∫ 0 1 x 2 d x \int_0^1x^2dx ∫01x2dx :将 [ 0 , 1 ] [0,1] [0,1] n等分,分点为 x i = i n , ( i = 1 , 2 , ⋯ , n ) x_i=\frac{i}{n},(i=1,2,\cdots,n) xi=ni,(i=1,2,⋯,n)
小区间 [ x i − 1 , x i ] [x_{i-1},x_i] [xi−1,xi] 的长度 Δ x i = 1 n , ( i = 1 , 2 , ⋯ , n ) \Delta x_i=\frac{1}{n},(i=1,2,\cdots,n) Δxi=n1,(i=1,2,⋯,n)
取 ξ i = x i \xi_i=x_i ξi=xi , ∑ i = 1 n f ( ξ i ) Δ x i = ∑ i = 1 n ξ i 2 Δ x i = ∑ i = 1 n ( i n ) 2 1 n = 1 n 3 ∑ i = 1 n i 2 = 1 n 3 n ( n + 1 ) ( 2 n + 1 ) 6 \sum_{i=1}^n f(\xi_i)\Delta x_i=\sum_{i=1}^n\xi_i^2\Delta x_i=\sum_{i=1}^n(\frac{i}{n})^2\frac{1}{n}=\frac{1}{n^3}\sum_{i=1}^ni^2=\frac{1}{n^3}\frac{n(n+1)(2n+1)}{6} ∑i=1nf(ξi)Δxi=∑i=1nξi2Δxi=∑i=1n(ni)2n1=n31∑i=1ni2=n316n(n+1)(2n+1)
∣ Δ x ∣ → 0 ⇒ n → ∞ \vert \Delta x\vert\rightarrow 0\Rightarrow n\rightarrow \infty ∣Δx∣→0⇒n→∞ , lim n → ∞ ( n + 1 ) ( 2 n + 1 ) 6 n 2 = 1 3 ⇒ ∫ 0 1 x 2 d x = ∑ i = 1 n f ( ξ i ) Δ x i = 1 3 \lim_{n\rightarrow \infty}\frac{(n+1)(2n+1)}{6n^2}=\frac{1}{3}\Rightarrow \int_0^1x^2dx=\sum_{i=1}^nf(\xi_i)\Delta x_i=\frac{1}{3} limn→∞6n2(n+1)(2n+1)=31⇒∫01x2dx=∑i=1nf(ξi)Δxi=31
定积分性质
∫ a b [ f ( x ) ± g ( x ) ] d x = ∫ a b f ( x ) d x ± ∫ a b g ( x ) d x \int_{a}^b[f(x)\pm g(x)]dx=\int_a^bf(x)dx\pm \int_a^bg(x)dx ∫ab[f(x)±g(x)]dx=∫abf(x)dx±∫abg(x)dx
∫ a b k f ( x ) d x = k ∫ a b f ( x ) d x , ( k 为常数 ) \int_a^bkf(x)dx=k\int_a^bf(x)dx,(k为常数) ∫abkf(x)dx=k∫abf(x)dx,(k为常数)
∫ a b f ( x ) d x = ∫ a c f ( x ) d x + ∫ c b f ( x ) d x \int_a^b{f(x)}dx=\int_a^cf(x)dx+\int_c^bf(x)dx ∫abf(x)dx=∫acf(x)dx+∫cbf(x)dx
若 [ a , b ] [a,b] [a,b] 上, f ( x ) ≥ 0 ⇒ ∫ a b f ( x ) d x ≥ 0 , ( a < b ) f(x)\ge 0\Rightarrow \int_a^bf(x)dx\ge 0,(a
定理
积分第一中值定理: f ( x ) f(x) f(x) 在 [ a , b ] [a,b] [a,b] 上连续,则在 [ a , b ] [a,b] [a,b] 上至少存在一点 ξ \xi ξ ,使 ∫ a b f ( x ) d x = f ( ξ ) ( b − a ) \int_a^b f(x)dx=f(\xi)(b-a) ∫abf(x)dx=f(ξ)(b−a)
积分上限函数: f ( x ) f(x) f(x) 在 [ a , b ] [a,b] [a,b] 上连续,对于定积分 ∫ a x f ( x ) d x \int_a^x f(x)dx ∫axf(x)dx 每个取值 f ( x ) f(x) f(x) 有一个值 Φ ( x ) = ∫ a x f ( t ) d t \Phi(x)=\int_a^x f(t)dt Φ(x)=∫axf(t)dt
N-L公式
F ( x ) F(x) F(x) 连续且未 f ( x ) f(x) f(x) 在 [ a , b ] [a,b] [a,b] 上原函数, ∫ a b f ( x ) d x = F ( b ) − F ( a ) \int_{a}^bf(x)dx =F(b)-F(a) ∫abf(x)dx=F(b)−F(a)
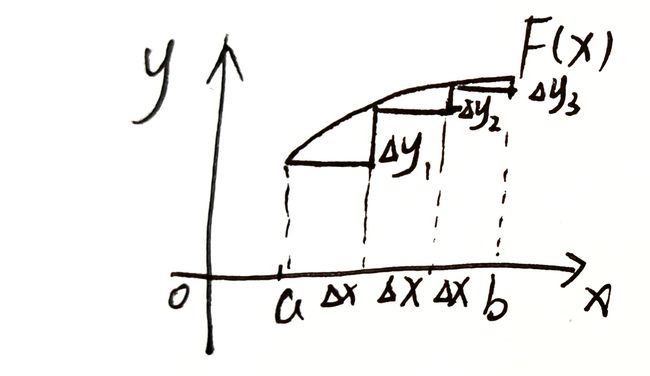
几何意义:
F ( b ) − F ( a ) = ∑ Δ y i F(b)-F(a)=\sum\Delta y_i F(b)−F(a)=∑Δyi
当 Δ x → 0 \Delta x\rightarrow 0 Δx→0 时,有 d y i ≈ Δ y i , F ′ ( x ) = d F ( x ) d x = d y d x dy_i\approx \Delta y_i,F'(x)=\frac{dF(x)}{dx}=\frac{dy}{dx} dyi≈Δyi,F′(x)=dxdF(x)=dxdy
∴ F ( b ) − F ( a ) = ∑ Δ y i = ∑ d y i = ∑ f ( x ) d x = ∫ a b f ( x ) d x \therefore\quad F(b)-F(a)=\sum\Delta y_i=\sum dy_i=\sum f(x)dx=\int_a^bf(x)dx ∴F(b)−F(a)=∑Δyi=∑dyi=∑f(x)dx=∫abf(x)dx
基本公式
∫ a b f ( x ) d x = f ( ξ ) ( b − a ) ⏟ 积分中值定理 = F ′ ( ξ ) ( b − a ) ⏟ 微分中值定理 = F ( b ) − F ( a ) \underbrace{\int_{a}^bf(x)dx=f(\xi)(b-a)}_{积分中值定理}=\underbrace{F'(\xi)(b-a)}_{微分中值定理}=F(b)-F(a) 积分中值定理 ∫abf(x)dx=f(ξ)(b−a)=微分中值定理 F′(ξ)(b−a)=F(b)−F(a)
泰勒公式
以直代曲:多项式代替原函数
常用泰勒公式
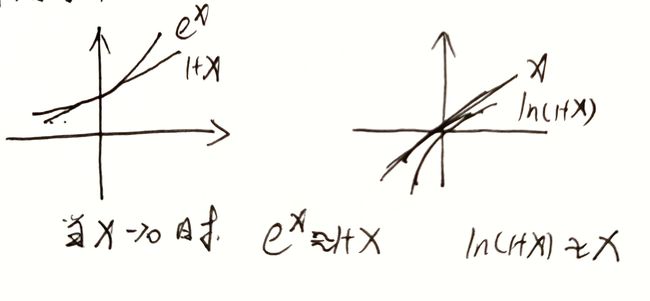
当 x → 0 x\rightarrow 0 x→0 时, e x ≈ 1 + x e^x\approx 1+x ex≈1+x , l n ( 1 + x ) ≈ x ln(1+x)\approx x ln(1+x)≈x
P n ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) ( x − x 0 ) 2 2 ! + f ′ ′ ′ ( x 0 ) ( x − x 0 ) 3 3 ! + ⋯ + f ( n ) ( x 0 ) ( x − x 0 ) n n ! P_n(x)=f(x_0)+f'(x_0)(x-x_0)+f''(x_0)\frac{(x-x_0)^2}{2!}+f'''(x_0)\frac{(x-x_0)^3}{3!}+\cdots+f^{(n)}(x_0)\frac{(x-x_0)^n}{n!} Pn(x)=f(x0)+f′(x0)(x−x0)+f′′(x0)2!(x−x0)2+f′′′(x0)3!(x−x0)3+⋯+f(n)(x0)n!(x−x0)n
导数作用
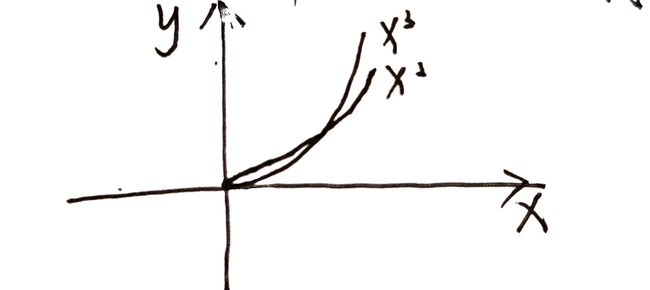
阶越高,增长速度越快
低阶能更好描述当前点,阶越高在右侧影响越大
阶乘作用
在低阶,保证 x 5 , x 6 x^5,x^6 x5,x6 次项作用(高次项) x + x 2 2 ! + ⋯ + x 5 5 ! x+\frac{x^2}{2!}+\cdots+\frac{x^5}{5!} x+2!x2+⋯+5!x5
在高阶,保证 x , x 2 x,x^2 x,x2 次项作用(低次项)
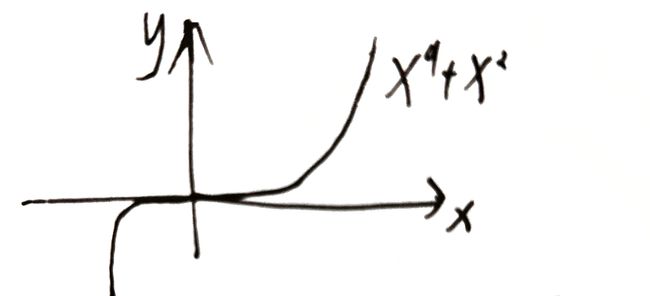
若无阶乘,高阶压制低阶,函数呈高次项特性
如: x 9 + x 2 x^9+x^2 x9+x2
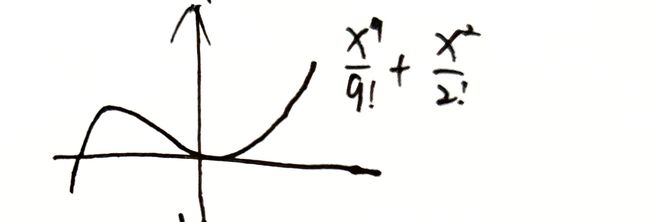
引入阶乘,图像先呈现 x 2 x^2 x2 特性,再呈现 x 9 x^9 x9 特性
x x x 小时, 1 9 ! \frac{1}{9!} 9!1 可限制 x 9 x^9 x9 项
随 x x x 增加, 1 9 ! \frac{1}{9!} 9!1 作用变小,无法再限制 x 9 x^9 x9
麦克劳林公式
f ( x ) = f ( 0 ) + f ′ ( 0 ) x + f ′ ′ ( 0 ) x 2 2 ! + ⋯ + f ( n ) x n n ! + f ( n + 1 ) ( θ x ) x ( n + 1 ) ( n + 1 ) ! , 0 < θ < 1 f(x)=f(0)+f'(0)x+f''(0)\frac{x^2}{2!}+\cdots+f^{(n)}\frac{x^n}{n!}+f^{(n+1)}(\theta x)\frac{x^{(n+1)}}{(n+1)!},0<\theta < 1 f(x)=f(0)+f′(0)x+f′′(0)2!x2+⋯+f(n)n!xn+f(n+1)(θx)(n+1)!x(n+1),0<θ<1
-
s i n x = f ′ ( 0 ) x − x 3 3 ! f ( 3 ) ( 0 ) + x 5 5 ! f ( 5 ) ( 0 ) − ⋯ = x − x 3 3 ! + x 5 5 ! + ⋯ + ( − 1 ) ( n − 1 ) x ( 2 n − 1 ) 2 n − 1 sinx=f'(0)x-\frac{x^3}{3!}f^{(3)}(0)+\frac{x^5}{5!}f^{(5)}(0)-\cdots=x-\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots+(-1)^{(n-1)}\frac{x^{(2n-1)}}{2n-1} sinx=f′(0)x−3!x3f(3)(0)+5!x5f(5)(0)−⋯=x−3!x3+5!x5+⋯+(−1)(n−1)2n−1x(2n−1)
R n + 1 = ( − 1 ) n c o s ( θ x ) ( 2 n + 1 ) ! x ( 2 n + 1 ) , ( 0 < θ < 1 ) R_{n+1}=(-1)^{n}\frac{cos(\theta x)}{(2n+1)!}x^{(2n+1)},(0<\theta < 1) Rn+1=(−1)n(2n+1)!cos(θx)x(2n+1),(0<θ<1)
1.5 求极值
1.5.1 无条件极值
z = f ( x , y ) z=f(x,y) z=f(x,y) 在 P 0 P_0 P0 邻域内连续,且有一阶、二阶偏导数,求 z z z 在邻域内的极值
求解:
令 f x ( x , y ) = 0 , f y ( x , y ) = 0 ⇒ P 0 ( x 0 , y 0 ) f_x(x,y)=0,f_y(x,y)=0\Rightarrow P_0(x_0,y_0) fx(x,y)=0,fy(x,y)=0⇒P0(x0,y0)
令 A = f x x ( x , y ) ∣ P 0 A=f_{xx}(x,y)\vert _{P_0} A=fxx(x,y)∣P0 , B = f x y ( x , y ) ∣ P 0 B=f_{xy}(x,y)\vert_{P_0} B=fxy(x,y)∣P0 , C = f y y ( x , y ) ∣ P 0 C=f_{yy}(x,y)\vert_{P_0} C=fyy(x,y)∣P0
若
- A C − B 2 > 0 AC-B^2>0 AC−B2>0 ,则 f ( x , y ) f(x,y) f(x,y) 在 P 0 P_0 P0 处为极值点
- A > 0 A>0 A>0 ,则为极小值
- A < 0 A<0 A<0 ,则为极大值
- A C − B 2 < 0 AC-B^2<0 AC−B2<0 ,则 f ( x , y ) f(x,y) f(x,y) 在 P 0 P_0 P0 处不是极值点
- A C − B 2 = 0 AC-B^2=0 AC−B2=0 ,待定
1.5.2 条件极值
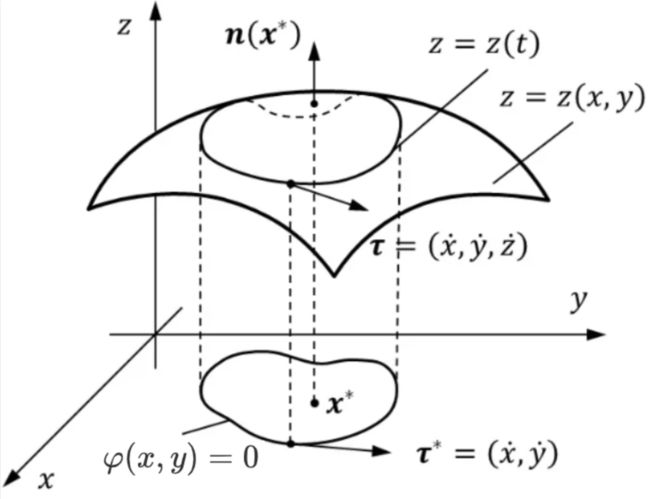
x , y x,y x,y 满足 φ ( x , y ) = 0 φ ( x , y ) = 0 \varphi(x,y)=0\varphi(x,y)=0 φ(x,y)=0φ(x,y)=0 , 求 z = f ( x , y ) z=f(x,y) z=f(x,y) 的极值
φ ( x , y ) = 0 \varphi(x,y)=0 φ(x,y)=0 为 x o y xoy xoy 面上的曲线,将 φ ( x , y ) = 0 \varphi(x,y)=0 φ(x,y)=0 投影到曲面 z = f ( x , y ) z=f(x,y) z=f(x,y) 上,有曲线 Γ ( x , y , z ) \Gamma(x,y,z) Γ(x,y,z) 。
在曲线 Γ \Gamma Γ 上找极值点为一个无条件极值问题,故用一个独立参数 t t t 表示曲线 Γ \Gamma Γ 不受任何约束,即 { x = x ( t ) y = y ( t ) \left\{\begin{aligned}x=x(t)\\y=y(t)\end{aligned}\right. {x=x(t)y=y(t) ,有 z = { x ( t ) , y ( t ) } ⇒ z = z ( t ) z=\{x(t),y(t)\}\Rightarrow z=z(t) z={x(t),y(t)}⇒z=z(t)
极值条件:
{ d z d t = 0 ⟺ ∂ z ∂ x x ′ ( t ) + ∂ z ∂ y y ′ ( t ) = 0 d φ d t = 0 ⟺ ∂ φ ∂ x x ′ ( t ) + ∂ φ ∂ y y ′ ( t ) = 0 ⇒ y ′ ( t ) = − ∂ φ ∂ x ∂ φ ∂ y x ′ ( t ) [ ∂ z ∂ x − ∂ z ∂ y ∂ φ ∂ x ∂ φ ∂ y ] x ′ ( t ) = 0 [ ∂ z ∂ x ∂ φ ∂ y − ∂ z ∂ y ∂ ϕ ∂ x ] x ′ ( t ) = 0 ⟺ ( ∂ z ∂ x , ∂ z ∂ y ) ⋅ ( ∂ φ ∂ y , − ∂ φ ∂ x ) = 0 ⟺ ▽ z ( x , y ) ⋅ ( ∂ φ ∂ y , − ∂ φ ∂ x ) = 0 \begin{aligned} \left\{ \begin{aligned} \frac{dz}{dt}=0\iff \frac{\partial z}{\partial x}x'(t)+\frac{\partial z}{\partial y}y'(t)=0\\ \frac{d\varphi}{dt}=0\iff \frac{\partial \varphi}{\partial x}x'(t)+\frac{\partial \varphi}{\partial y}y'(t)=0 \end{aligned} \right.\\ \xRightarrow{y'(t)=-\frac{\frac{\partial \varphi}{\partial x}}{\frac{\partial \varphi}{\partial y}}x'(t)} \left[\frac{\partial z}{\partial x}-\frac{\partial z}{\partial y}\frac{\frac{\partial \varphi}{\partial x}}{\frac{\partial \varphi}{\partial y}}\right]x'(t)=0\\ \left[\frac{\partial z}{\partial x}\frac{\partial \varphi}{\partial y}-\frac{\partial z}{\partial y}\frac{\partial \phi}{\partial x}\right]x'(t)=0\\ \iff\left(\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}\right)\cdot\left(\frac{\partial \varphi}{\partial y},-\frac{\partial \varphi}{\partial x}\right)=0\\ \iff \bigtriangledown z(x,y) \cdot \left(\frac{\partial \varphi}{\partial y},-\frac{\partial \varphi}{\partial x}\right)=0 \end{aligned} ⎩ ⎨ ⎧dtdz=0⟺∂x∂zx′(t)+∂y∂zy′(t)=0dtdφ=0⟺∂x∂φx′(t)+∂y∂φy′(t)=0y′(t)=−∂y∂φ∂x∂φx′(t)[∂x∂z−∂y∂z∂y∂φ∂x∂φ]x′(t)=0[∂x∂z∂y∂φ−∂y∂z∂x∂ϕ]x′(t)=0⟺(∂x∂z,∂y∂z)⋅(∂y∂φ,−∂x∂φ)=0⟺▽z(x,y)⋅(∂y∂φ,−∂x∂φ)=0
显然,有 ( ∂ φ ∂ y , − ∂ φ ∂ x ) \left(\frac{\partial \varphi}{\partial y},-\frac{\partial \varphi}{\partial x}\right) (∂y∂φ,−∂x∂φ) 与 ▽ ϕ = ( ∂ φ ∂ x , ∂ φ ∂ y ) \bigtriangledown \phi=\left(\frac{\partial \varphi}{\partial x},\frac{\partial \varphi}{\partial y}\right) ▽ϕ=(∂x∂φ,∂y∂φ) 垂直
故可得结论:极值点处满足 ▽ z \bigtriangledown z ▽z 与 ▽ φ \bigtriangledown \varphi ▽φ 共线,即 ▽ z + λ ▽ φ = 0 ⇒ ▽ [ z ( x , y ) + λ φ ( x , y ) ] = 0 \bigtriangledown z+\lambda \bigtriangledown \varphi=0\Rightarrow \bigtriangledown\left[z(x,y)+\lambda\varphi(x,y)\right]=0 ▽z+λ▽φ=0⇒▽[z(x,y)+λφ(x,y)]=0
限制条件 : φ ( x , y ) = 0 限制条件下的无条件极值 : f x ( x , y ) + λ φ x ( x , y ) = 0 f y ( x , y ) + λ φ y ( x , y ) = 0 } ⇒ { x 0 = y 0 = λ = ∴ ( x 0 , y 0 ) 为 z = f ( x , y ) 在条件 φ ( x , y ) = 0 下的极值点 \begin{aligned} &\left. \begin{aligned} &限制条件:\varphi(x,y)=0\\ &限制条件下的无条件极值:\\ &\quad f_x(x,y)+\lambda\varphi_x(x,y)=0\\ &\quad f_y(x,y)+\lambda\varphi_y(x,y)=0\\ \end{aligned} \right\} \Rightarrow\left\{ \begin{aligned} x_0=\\y_0=\\\lambda= \end{aligned} \right.\\ &\therefore (x_0,y_0) 为 z=f(x,y)在条件 \varphi(x,y)=0下的极值点 \end{aligned} 限制条件:φ(x,y)=0限制条件下的无条件极值:fx(x,y)+λφx(x,y)=0fy(x,y)+λφy(x,y)=0⎭ ⎬ ⎫⇒⎩ ⎨ ⎧x0=y0=λ=∴(x0,y0)为z=f(x,y)在条件φ(x,y)=0下的极值点
1.5.3 多条件极值
u = f ( x , y , z , t ) u=f(x,y,z,t) u=f(x,y,z,t) 在条件 φ ( x , y , z , t ) = 0 , ψ ( x , y , z , t ) = 0 \varphi(x,y,z,t)=0,\psi(x,y,z,t)=0 φ(x,y,z,t)=0,ψ(x,y,z,t)=0 下的极值,构造函数 F ( x , y , z , t ) = f ( x , y , z , t ) + λ 1 φ ( x , y , z , t ) + λ 2 ψ ( x , y , z , t ) F(x,y,z,t)=f(x,y,z,t)+\lambda_1\varphi(x,y,z,t)+\lambda_2\psi(x,y,z,t) F(x,y,z,t)=f(x,y,z,t)+λ1φ(x,y,z,t)+λ2ψ(x,y,z,t)
eg1
u = x 3 y 2 z , x + y + z = 12 u=x^3y^2z,x+y+z=12 u=x3y2z,x+y+z=12 ,求最大值
构造拉格朗日函数 F ( x , y , z , t ) = x 3 y 2 z + λ ( x + y + z − 12 ) = 0 F(x,y,z,t)=x^3y^2z+\lambda(x+y+z-12)=0 F(x,y,z,t)=x3y2z+λ(x+y+z−12)=0
令 { F x ′ = 3 x 2 y 2 z + λ = 0 F y ′ = 2 x 3 y z + λ = 0 F z ′ = x 3 y 2 + λ = 0 x + y + z = 12 ⇒ { x 0 = 6 y 0 = 4 z 0 = 2 \left\{\begin{aligned}&F_x'=3x^2y^2z+\lambda=0\\&F_y'=2x^3yz+\lambda=0\\&F_z'=x^3y^2+\lambda=0\\&x+y+z=12\end{aligned}\right.\Rightarrow \left\{\begin{aligned}x_0=6\\y_0=4\\z_0=2\end{aligned}\right. ⎩ ⎨ ⎧Fx′=3x2y2z+λ=0Fy′=2x3yz+λ=0Fz′=x3y2+λ=0x+y+z=12⇒⎩ ⎨ ⎧x0=6y0=4z0=2
1.5.4 凹函数与凸函数
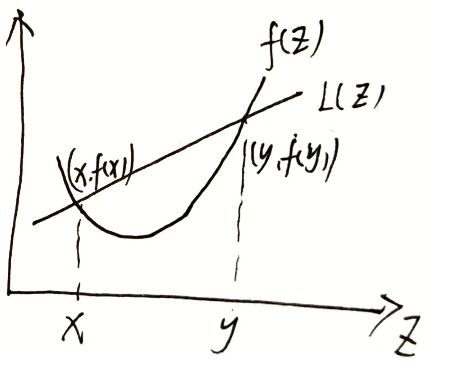
已知两点 ( x , f ( x ) ) (x,f(x)) (x,f(x)) , ( y , f ( y ) ) (y,f(y)) (y,f(y)) ,验证 f ( t x + ( 1 − t ) y ) ≤ t f ( x ) + ( 1 − t ) f ( y ) , t ∈ ( 0 , 1 ] f(tx+(1-t)y)\le tf(x)+(1-t)f(y),t\in (0,1] f(tx+(1−t)y)≤tf(x)+(1−t)f(y),t∈(0,1] ,则 f ( z ) f(z) f(z) 为凸函数
设直线 L ( z ) L(z) L(z) 为 Y − f ( x ) = f ( y ) − f ( x ) y − x ( X − x ) Y-f(x)=\frac{f(y)-f(x)}{y-x}(X-x) Y−f(x)=y−xf(y)−f(x)(X−x)
在 [ x , y ] [x,y] [x,y] 中间的任一点横坐标可表示为 t x + ( 1 − t ) y tx+(1-t)y tx+(1−t)y ,代入后直线方程可得 Y = f ( y ) − f ( x ) y − x [ t x + ( 1 − t ) y − x ] + f ( x ) = f ( y ) − f ( x ) y − x ( 1 − t ) ( y − x ) + f ( x ) = t f ( x ) + ( 1 − t ) f ( y ) Y=\frac{f(y)-f(x)}{y-x}[tx+(1-t)y-x]+f(x)=\frac{f(y)-f(x)}{y-x}(1-t)(y-x)+f(x)=tf(x)+(1-t)f(y) Y=y−xf(y)−f(x)[tx+(1−t)y−x]+f(x)=y−xf(y)−f(x)(1−t)(y−x)+f(x)=tf(x)+(1−t)f(y)
若某一自变量曲线上值 f ( z ) f(z) f(z) 小于直线上值 L ( z ) L(z) L(z) , 即满足 f ( t x + ( 1 − t ) y ) ≤ t f ( x ) + ( 1 − t ) f ( y ) , t ∈ ( 0 , 1 ] f(tx+(1-t)y)\le tf(x)+(1-t)f(y),t\in (0,1] f(tx+(1−t)y)≤tf(x)+(1−t)f(y),t∈(0,1] ,函数 f ( z ) f(z) f(z) 为凸函数
易于沿梯度寻找最优值,作为激活函数