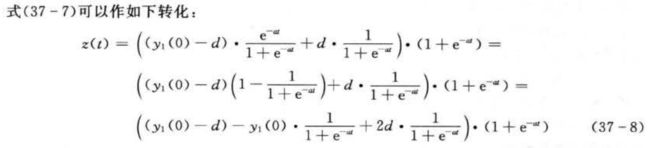基于灰色神经网络的订单需求预测Matlab代码
1.案例背景
1.1 灰色理论
灰色系统理论是一种研究少数据、贫信息,不确定性问题的新方法,它以部分信息已知、部分信息未知的“小样本”、“贫信息"不确定系统为研究对象,通过对“部分”已知信息的生成、开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控。
灰色理论是我国学者邓聚龙教授在1982年首先提出的,该理论认为任何随机过程都可看做是在一定时空区域内变化的灰色过程,随机量可看成灰色量,同时,他认为通过生成变换可将系统数据无规律的序列变成有规律的序列。灰色理论强调通过对无规律的系统已知信息的研究,提炼和挖掘有价值的信息,进而用已知信息去揭示未知信息,使系统不断“白化”。
灰色系统中建立的模型称为灰色模型(grey model,GM),该模型是以原始数据序列为基础建立的微分方程。灰色建模中最有代表性的模型是针对时间序列的GM建模。它直接将时间序列数据转化为微分方程,利用系统信息,使抽象的模型量化,进而在缺乏系统特性知识的情况下预测系统输出。
GM模型首先对原始数据序列做一次累加,使累加后的数据呈现一定规律,然后用典型曲线拟合该曲线。设有时间数据序列X(0):
1.2 灰色神经网络
灰色问题是指对灰色的不确定系统行为特征值的发展变化进行预测的问题,该不确定系
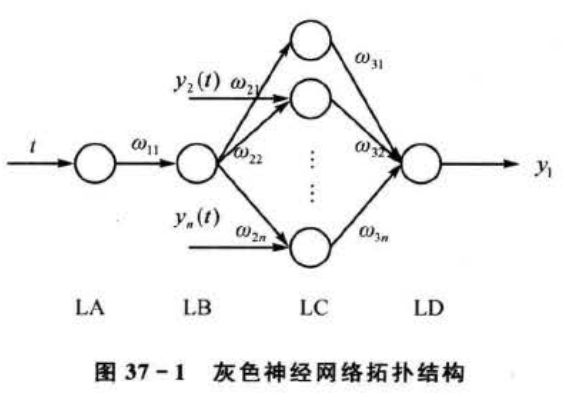
将变换后的式(37-8)映射到一个扩展的BP神经网络中就得到n个输人参数、1个输出参数的灰色神经网络,网络拓扑结构如图37-1所示。
1.3 冰箱订单预测
对于冰箱市场来说,影响其需求量的因素很多,比如季节性因素、成本、产品质量水平、品牌认可,售后服务、产品结构,产品生命周期、价格波动及销售力度、竞争对手,市场特征、性能价格比等,根据各因素对订单需求影响的大小,从中选取需求趋势、产品的市场份额、销售价格波动、订单缺货情况和分销商的联合预测情况5个因素作为主要因素预测冰箱订单量。
产品的市场份额是指某个企业销售额在同一市场(或行业)全部销售额中所占比重。一般来说,某市场中,企业越多,单个企业所占比重越低,即市场份额小,该市场的竞争程度越高。
产品的生命周期是指产品从推出市场到从市场退出的周期。产品订单同产品生命周期有很大关系,比如产品处于成长期,那么其需求将增长快速。处于成熟期,其需求的增长比较缓慢且稳定。
价格波动一般指企业为了增加产品的销量,减少闲置库存,提升品牌竞争力,又或者由于原材料的成本增加﹐为满足一定的盈利,短期时间内价格的变化。价格的波动导致的需求量突增或突减可反映在市场活动如促销前后,直接的价格战前后,因而在做需求预测时要考虑预测期间的市场活动状况,对预测的需求量按促销等力度加以调整。
订单满足率是指由于供应量的不足导致的缺货和其他原因不能满足给定数量的货物所占总订单数的比例。对于某冰箱公司,一般情况下,下游企业或者说批发商会在给定前置期的范围内下订单,但是由于月前的以需求计划为引导的生产计划可能不能满足足够数额的需求,所以会产生制造商和批发商之间的短期博弈。
分销商联合预测因素是指供应商、制造商,配送商、分销商,零售商直至最后的客户连接成一个有机体,考虑各自上下游之间的需求匹配性,进行联合预测,实现信息共享,来减少供应链中的存货、生产及运输成本,快速响应消费者需求,提高订单满足率和客户服务水平。
2.模型建立
基于灰色神经网络的冰箱订单预测算法流程如图37-2所示。其中,灰色神经网络构建根据输人/输出数据维数确定灰色神经网络结构。由于本案例输入数据为5维,输出为1维,所以灰色神经网络结构为1—1—6—1,即LA层有1个节点,输人为时间序列t,LB层有1个节点,LC层有6个节点,第2~6个分别输人市场份额、需求趋势、价格波动、订单满足率、分销商联合预测5个因素的归一化数据,输出为预测订单量。
灰色神经网络训练用训练数据训练灰色神经网络,使网络具有订单预测能力。灰色神经网络预测用网络预测订单数量,并根据预测误差判断网络性能。共有过去3年(36个月)的数据,首先取前30个月的数据作为训练数据训练网络,网络共学习进化100次,然后用剩余6组数据评价网络的预测性能。
3.编程实现
根据灰色神经网络原理,在MATLAB中编程实现基于灰色神经网络的订单需求预测。
%% 该代码为基于灰色神经网络的预测算法
%% 清空环境变量
clc
clear
load data
%% 数据累加作为网络输入
[n,m]=size(X);
for i=1:n
y(i,1)=sum(X(1:i,1));
y(i,2)=sum(X(1:i,2));
y(i,3)=sum(X(1:i,3));
y(i,4)=sum(X(1:i,4));
y(i,5)=sum(X(1:i,5));
y(i,6)=sum(X(1:i,6));
end
%% 网络参数初始化
a=0.3+rand(1)/4;
b1=0.3+rand(1)/4;
b2=0.3+rand(1)/4;
b3=0.3+rand(1)/4;
b4=0.3+rand(1)/4;
b5=0.3+rand(1)/4;
%% 学习速率初始化
u1=0.0015;
u2=0.0015;
u3=0.0015;
u4=0.0015;
u5=0.0015;
%% 权值阀值初始化
t=1;
w11=a;
w21=-y(1,1);
w22=2*b1/a;
w23=2*b2/a;
w24=2*b3/a;
w25=2*b4/a;
w26=2*b5/a;
w31=1+exp(-a*t);
w32=1+exp(-a*t);
w33=1+exp(-a*t);
w34=1+exp(-a*t);
w35=1+exp(-a*t);
w36=1+exp(-a*t);
theta=(1+exp(-a*t))*(b1*y(1,2)/a+b2*y(1,3)/a+b3*y(1,4)/a+b4*y(1,5)/a+b5*y(1,6)/a-y(1,1));
kk=1;
%% 循环迭代
for j=1:10
%循环迭代
E(j)=0;
for i=1:30
%% 网络输出计算
t=i;
LB_b=1/(1+exp(-w11*t)); %LB层输出
LC_c1=LB_b*w21; %LC层输出
LC_c2=y(i,2)*LB_b*w22; %LC层输出
LC_c3=y(i,3)*LB_b*w23; %LC层输出
LC_c4=y(i,4)*LB_b*w24; %LC层输出
LC_c5=y(i,5)*LB_b*w25; %LC层输出
LC_c6=y(i,6)*LB_b*w26; %LC层输出
LD_d=w31*LC_c1+w32*LC_c2+w33*LC_c3+w34*LC_c4+w35*LC_c5+w36*LC_c6; %LD层输出
theta=(1+exp(-w11*t))*(w22*y(i,2)/2+w23*y(i,3)/2+w24*y(i,4)/2+w25*y(i,5)/2+w26*y(i,6)/2-y(1,1)); %阀值
ym=LD_d-theta; %网络输出值
yc(i)=ym;
%% 权值修正
error=ym-y(i,1); %计算误差
E(j)=E(j)+abs(error); %误差求和
error1=error*(1+exp(-w11*t)); %计算误差
error2=error*(1+exp(-w11*t)); %计算误差
error3=error*(1+exp(-w11*t));
error4=error*(1+exp(-w11*t));
error5=error*(1+exp(-w11*t));
error6=error*(1+exp(-w11*t));
error7=(1/(1+exp(-w11*t)))*(1-1/(1+exp(-w11*t)))*(w21*error1+w22*error2+w23*error3+w24*error4+w25*error5+w26*error6);
%修改权值
w22=w22-u1*error2*LB_b;
w23=w23-u2*error3*LB_b;
w24=w24-u3*error4*LB_b;
w25=w25-u4*error5*LB_b;
w26=w26-u5*error6*LB_b;
w11=w11+a*t*error7;
end
end
%画误差随进化次数变化趋势
figure(1)
plot(E)
title('训练误差','fontsize',12);
xlabel('进化次数','fontsize',12);
ylabel('误差','fontsize',12);
%print -dtiff -r600 28-3
%根据训出的灰色神经网络进行预测
for i=31:36
t=i;
LB_b=1/(1+exp(-w11*t)); %LB层输出
LC_c1=LB_b*w21; %LC层输出
LC_c2=y(i,2)*LB_b*w22; %LC层输出
LC_c3=y(i,3)*LB_b*w23; %LC层输出
LC_c4=y(i,4)*LB_b*w24; %LC层输出
LC_c5=y(i,5)*LB_b*w25;
LC_c6=y(i,6)*LB_b*w26;
LD_d=w31*LC_c1+w32*LC_c2+w33*LC_c3+w34*LC_c4+w35*LC_c5+w36*LC_c6; %LD层输出
theta=(1+exp(-w11*t))*(w22*y(i,2)/2+w23*y(i,3)/2+w24*y(i,4)/2+w25*y(i,5)/2+w26*y(i,6)/2-y(1,1)); %阀值
ym=LD_d-theta; %网络输出值
yc(i)=ym;
end
yc=yc*100000;
y(:,1)=y(:,1)*10000;
%计算预测的每月需求量
for j=36:-1:2
ys(j)=(yc(j)-yc(j-1))/10;
end
figure(2)
plot(ys(31:36),'-*');
hold on
plot(X(31:36,1)*10000,'r:o');
legend('灰色神经网络','实际订单数')
title('灰色系统预测','fontsize',12)
xlabel('月份','fontsize',12)
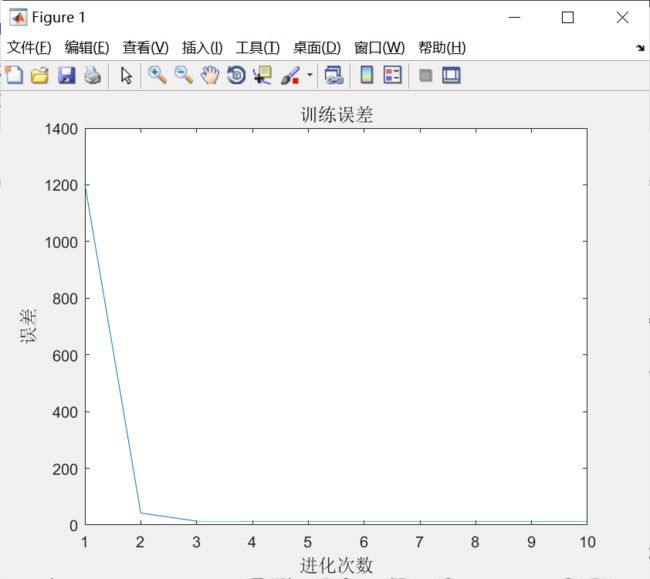
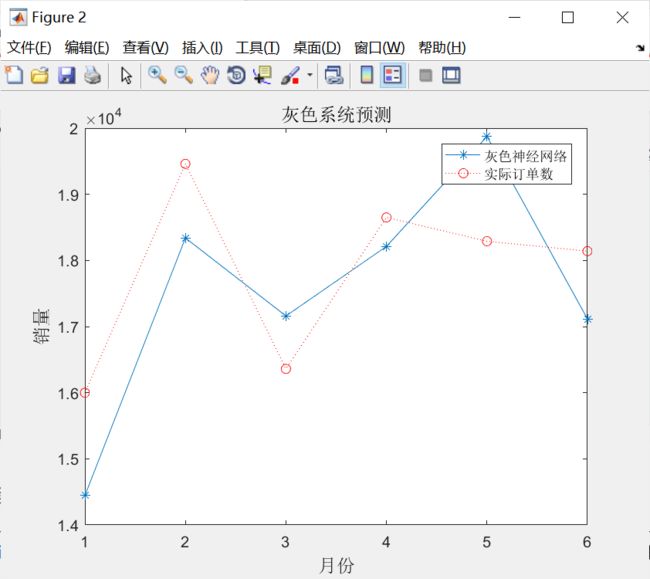
ylabel('销量','fontsize',12)运行结果如下:
从图可以看出,灰色神经网络收敛速度很快,但是网络很快陷人局部最优,无法进一步修正参数。用训练好的灰色神经网络预测冰箱订单,灰色神经网络预测的平均误差为7.20%,说明灰色神经比较适用于小样本预测问题。
4.完整数据文件
下载链接:
【免费】基于灰色神经网络的订单需求预测Matlab代码