论文解读《Adversarial training methods for semi-supervised text classification》
1 背景
1.1 对抗性实例(Adversarial examples)
- 通过对输入进行小扰动创建的实例,可显著增加机器学习模型所引起的损失
- 对抗性实例的存在暴露了机器学习模型的脆弱性和局限性,也对安全敏感的应用场景带来了潜在的威胁;
1.2 对抗性训练
训练模型正确分类未修改示例和对抗性示例的过程,使分类器对扰动具有鲁棒性
目的:
-
- 正则化手段,提升模型的性能(分类准确率),防止过拟合
- 产生对抗样本,攻击深度学习模型,产生错误结果(错误分类)
- 让上述的对抗样本参与的训练过程中,提升对对抗样本的防御能力,具有更好的泛化能力
- 利用 GAN 来进行自然语言生成 有监督问题中通过标签将对抗性扰动设置为最大化
1.3 虚拟对抗性训练
将对抗性训练扩展到半监督/无标记情况
使模型在某实例和其对抗性扰动上产生相同的输出分布
2 方法
2.1 整体框架
基本思想:扩展对抗性训练/虚拟对抗性训练至文本分类任务和序列模型
基本思路:
- 对于文本分类任务,由于输入是离散的,且常表示为高维one-hot向量,不允许无穷小的扰动,因此将扰动施加于词嵌入中;由于受干扰的嵌入不能映射至某个单词,本文中训练策略仅作为通过稳定分类函数来正则化文本分类器的方法,不能防御恶意扰动;
- 施加扰动于规范化的词嵌入中,设置对抗性损失/虚拟对抗性损失,增强模型分类的鲁棒性;
2.2 方法介绍
将离散单词输入转化为连续向量,定义单词嵌入矩阵:
R(K+1)×DR(K+1)×D
其中 KK 指代单词数量,第 K+1K+1 个单词嵌入作为序列 结束(eoseos)令牌
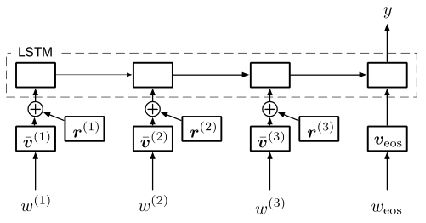
设置对应时间步长的离散单词为 w(t)w(t) ,单词嵌入为 v(t)v(t)
针对文本分类问题使用 LSTM 模型或双向 LSTM 模型 由于扰动为有界范数,模型在对抗性训练过程中可能 通过 “学习具有较大范数的嵌入使扰动变得不重要” 的病态解决方案,因此需将嵌入进行规范化:
v¯¯¯k=vk−E(v)Var(v)√ where E(v)=∑Kj=1fjvj,Var(v)=∑Kj=1fj(vj−E(v))2v¯k=vk−E(v)Var(v) where E(v)=∑j=1Kfjvj,Var(v)=∑j=1Kfj(vj−E(v))2
其中 fifi 表示第 ii 个单词的频率,在所有训练示例中进行计算。
2.2.1 对抗性训练
对抗性训练尝试提高分类器对小的、近似最坏情况扰动的鲁棒性——使分类器预测误差最大
代价函数:
−logp(y∣x+rzdv;θ) where rudv−argminr,∣r∥≤ϵlogp(y∣x+r;θ^)−logp(y∣x+rzdv;θ) where rudv−argminr,∣r‖≤ϵlogp(y∣x+r;θ^)
其中 rr 为扰动, θˆθ^ 为分类器当前参数的常数集,即表明构造对抗性实例的过程中不应该进行反向传播修改参数
对抗性扰动 rr 的生成:通过线性逼近得到
radv=−ϵg/∥g∥2 where g=∇xlogp(y∣x;θ^)radv=−ϵg/‖g‖2 where g=∇xlogp(y∣x;θ^)
2.2.2 虚拟对抗性训练
将对抗性训练应用于半监督学习——使分类器预测的输出分布差距最大
额外代价:
KL[p(⋅∣x;θ^)∣p(⋅∣x+rv-adv ;θ)] where rv-adv =argmaxr,∥r∥≤ℓKL[p(⋅∣x;θ^)∥p(⋅∣x+r;θ^)]KL[p(⋅∣x;θ^)∣p(⋅∣x+rv-adv ;θ)] where rv-adv =argmaxr,‖r‖≤ℓKL[p(⋅∣x;θ^)‖p(⋅∣x+r;θ^)]
对抗性扰动设置:
radv=−ϵg/∥g∥2 where g=∇slogp(y∣s;θ^)radv=−ϵg/‖g‖2 where g=∇slogp(y∣s;θ^)
对抗性损失:
Ladv(θ)=−1N∑Nn=1logp(yn∣sn+radv,n;θ)Ladv(θ)=−1N∑n=1Nlogp(yn∣sn+radv,n;θ)
其中 NN 为标记样本的数量
虚拟对抗性扰动设置:
rv-adv =ϵg/∥g∥2 where g=∇s+dKL[p(⋅∣s;θ^)∣p(⋅∣s+d;θ^)]rv-adv =ϵg/‖g‖2 where g=∇s+dKL[p(⋅∣s;θ^)∣p(⋅∣s+d;θ^)]
其中 dd 为小随机向量,实际通过有限差分法和幂迭代计算虚拟对抗性扰动
虚拟对抗性训练损失:
LV-adv (θ)=1N′∑N′n′=1KL[p(⋅∣sn′;θ^)∣p(⋅∣sn′+rv−ndv,n′;θ)]LV-adv (θ)=1N′∑n′=1N′KL[p(⋅∣sn′;θ^)∣p(⋅∣sn′+rv−ndv,n′;θ)]
其中 NN 为标记/未标记样本的数量之和
3 总结
略
4 其他
- 基于梯度的攻击: FGSM(Fast Gradient Sign Method) PGD(Project Gradient Descent) MIM(Momentum Iterative Method)
- 基于优化的攻击: CW(Carlini-Wagner Attack)
- 基于决策面的攻击: DEEPFOOL