机器学习笔记之核函数再回首：Nadarya-Watson核回归python手写示例

引言

本节从代码角度，介绍基于高维特征向量使用$\text{Nadaraya-Watson}$核回归的示例。

回顾：$\text{Nadaraya-Watson}$核回归

在注意力机制基本介绍中，我们提到过这种基于注意力机制权重的懒惰学习方法。该方法与注意力机制关联的核心操作有如下步骤：

通过核函数描述样本之间的关联关系

我们想要主观获取某陌生样本$x\in {\mathbb{R}}^p$与数据集内各样本$x^{(i)}\in \mathcal{D}=\{x^{(i)},y^{(i)}{\}}_{i=1}^N,x^{(i)}\in {\mathbb{R}}^p$之间的关联关系。而这种描述关联关系的操作，我们首先会想到内积：
$$x\cdot x^{(i)}=x^T[x^{(i)}]$$
如果涉及到一个非线性问题——或者说仅仅使用内积对关联关系的表达不够丰富，可以通过高维特征转换将非线性问题转化为高维线性问题：
$$\{\begin{array}{l}x\Rightarrow \varphi (x)\\ x^{(i)}=\varphi (x^{(i)})(i=1,2,\cdots ,N)\\ x^T[x^{(i)}]\Rightarrow [\varphi (x){]}^T\varphi (x^{(i)})\end{array}$$
将低维特征转化为高维特征同样存在弊端。在核方法思想与核函数中介绍过：映射后的特征结果$\varphi (x),$其特征维数远远超过原始特征维数$p$，甚至是无限维。在这种情况下去计算$[\varphi (x){]}^T\varphi (x^{(i)})$，其计算代价是无法估量的。而核技巧提供了一种简化运算的方式。关于核函数$\kappa (\cdot )$的定义表示如下：
$$\kappa \left[x,x^{(i)}\right]=⟨\varphi (x),\varphi (x^{(i)})⟩=[\varphi (x){]}^T\varphi (x^{(i)})$$
可以看出：核函数$\kappa (\cdot )$的自变量是未经过高维转换的原始特征；而对应函数是高维转换后的内积结果。因而该函数的作用可以简化运算。最终我们可以通过核函数描述$x$与数据集内所有样本$x^{(i)}(i=1,2,\cdots ,N)$之间的关联关系：
$$\kappa \left[x,x^{(i)}\right]i=1,2,\cdots ,N$$

使用$\text{Softmax}$函数对权重进行划分

此时已经得到$x$与所有样本$x^{(i)}$的核函数结果，这$N$个结果有大有小，数值大的意味着样本之间的关联程度高。从而可以将该关联关系描述成$x$与样本$x^{(i)}$对应标签结果$y^{(i)}$的权重$\mathcal{G}(x,x^{(i)})$：
$$\mathcal{G}(x,x^{(i)})=\frac{\kappa (x,x^{(i)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})}$$
关于权重$\mathcal{G}(x,x^{(i)})$,必然有如下结果:
$$\sum _{i=1}^N\mathcal{G}(x,x^{(i)})=\frac{{\sum }_{i=1}^N\kappa (x,x^{(i)})}{{\sum }_{i=1}^N\kappa (x,x^{(i)})}=1$$
为什么是$\text{Softmax}$函数呢——如果该核函数是一个指数函数。例如高斯核函数：
将大括号内的项视作${\Delta }^{(i)}$；
κ ( x , x ( i ) ) = exp ⁡ { − 1 2 σ 2 ∥ x − x ( i ) ∥ 2 ⏟ Δ ( i ) } \kappa (x,x^{(i)}) = \exp \left\{\underbrace{- \frac{1}{2 \sigma^2} \left\|x - x^{(i)} \right\|^2 }_{\Delta^{(i)}}\right\} κ(x,x(i))=exp⎩ ⎨ ⎧​Δ(i) −2σ21​ ​x−x(i) ​2​​⎭ ⎬ ⎫​
那么$\mathcal{G}(x,x^{(i)})$可表示为：
$$\mathcal{G}(x,x^{(i)})=\frac{\exp \{{\Delta }^{(i)}\}}{{\sum }_{j=1}^N\exp \{{\Delta }^{(j)}\}}=\text{Softmax}({\Delta }^{(i)})$$
最终可以得到如下权重向量：
$$\mathcal{G}(x,\mathcal{D})={\left[\frac{\kappa (x,x^{(1)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})},\cdots ,\frac{\kappa (x,x^{(N)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})}\right]}_{1\times N}$$

将权重与相应标签执行加权运算

得到权重向量$\mathcal{G}(x,\mathcal{D})$后，与对应标签向量$\mathcal{Y}=(y^{(1)},\cdots ,y^{(N)}{)}^T$做内积运算，得到关于陌生样本$x$的预测结果$f(x)$：
本质上就是关于标签$y^{(i)}(i=1,2,\cdots ,N)$的加权平均数~
$$\begin{array}{rl}f(x)& =\mathcal{G}(x,\mathcal{D})\cdot \mathcal{Y}\\ & =\frac{\kappa (x,x^{(1)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})}\cdot y^{(1)}+\cdots \frac{\kappa (x,x^{(N)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})}\cdot y^{(N)}\end{array}$$

$\text{Nadaraya-Watson}$核回归代码示例

关于径向基核函数与高斯核函数

在上述注意力机制基本介绍一节中，我们模糊了径向基核函数与高斯核函数的区别。这里提出一些新的认识。两种核函数的公式表示如下：
$$\{\begin{array}{l}\begin{array}{rl}& \text{RBF : }\kappa (x,x^{(i)})=\exp (-\gamma \cdot \Vert x-x^{(i)}{\Vert }^2)\\ & \text{Gaussian : }\kappa (x,x^{(i)})=\exp \left[-\frac{1}{2{\sigma }^2}\Vert x-x^{(i)}{\Vert }^2\right]\end{array}\end{array}$$
相比之下，径向基核函数它的参数$\gamma \in [0,1]$，相比高斯核函数$\sigma$的范围描述的更加方便。

关于高维向量的核函数表示

根据上面公式，高维向量的核函数表示，其核心步骤是范数的表示。可以使用numpy模块中的numpy.linalg.norm()方法进行表示。下面分别通过调用径向基核函数模块：sklearn.metrics.pairwise.rbf_kernel以及手写方式进行实现：

import numpy as np
from sklean.metrics.pairwise import rbf_kernel

def RBFKernelFunction(xInput, xSample, gamma):
    def NormCalculation(xInput, xSample):
        NormResult = np.linalg.norm(xInput - xSample)
        return NormResult ** 2
    return np.exp((-1 * gamma) * NormCalculation(xInput, xSample))

a = np.array([1,2,3,4])
b = np.array([5,6,7,4])

SklearnOut = rbf_kernel(a.reshape(1,-1),b.reshape(1,-1),gamma=0.5)
ManuOut = RBFKernelFunction(a.reshape(1,-1),b.reshape(1,-1),gamma=0.5)
# [[3.77513454e-11]]
print(SklearnOut)
# 3.775134544279111e-11
print(ManuOut)

关于回归任务的相关示例

完整代码如下：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math
from tqdm import tqdm

def ReadXlsx(Path):
    Df = pd.read_excel(Path,sheet_name="Sheet1")
    return Df

def DealTokenAndLabel(Df):

    def DivideTokenAndLabel(ListInput):
        Label = ListInput.pop(3)
        return ListInput,Label

    def LinearCorrectOperation(Input,mode="Token"):
        assert mode in ["Token","Label"]
        if mode == "Token":
            OriginalToken = Input[3]
            UpdateToken = OriginalToken / 10.0
            Input[3] = round(UpdateToken,3)
        else:
            UpdateLabel = Input * 10.0
            Input = round(UpdateLabel,4)
        return Input

    DataList = list()
    LabelList = list()
    for (Ids,i) in Df.iterrows():
        Token,Label = DivideTokenAndLabel(list(i))
        UpdateToken = LinearCorrectOperation(Token)
        UpdateLabel = LinearCorrectOperation(Label,mode="Label")
        DataList.append(np.array(UpdateToken))
        LabelList.append(np.array(UpdateLabel))
    return DataList,LabelList

def AlgorithmProcess(DataList,LabelList,gamma,mode="RBF"):

    assert mode in ["Linear","RBF"]

    def RBFKernelFunction(xInput,xSample,gamma):

        def NormCalculation(xInput, xSample):
            NormResult = np.linalg.norm(xInput - xSample)
            return NormResult ** 2

        return np.exp((-1 * gamma) * NormCalculation(xInput, xSample))

    def LinearKernelFunction(xInput,xSample):

        return np.dot(xInput,xSample)

    def SoftmaxFunction(xInput,xSample,gamma,mode):

        if mode == "Linear":
            return LinearKernelFunction(xInput,xSample) / sum(LinearKernelFunction(xInput,i) for i in DataList)
        else:
            return RBFKernelFunction(xInput,xSample,gamma) / sum(RBFKernelFunction(xInput,i,gamma) for i in DataList)


    def NWKernalRegressionResult(xInput,gamma,mode):
        KernelRegressionList = list()
        for _,(TokenSample,LabelSample) in enumerate(zip(DataList,LabelList)):
            if (TokenSample == xInput).all():
                continue
            else:
                if mode == "RBF":
                    xInput = xInput.reshape(1, -1)
                    TokenSample = TokenSample.reshape(1, -1)

                SoftmaxCoeff = SoftmaxFunction(xInput, TokenSample, gamma, mode)
                KernelRegressionList.append(SoftmaxCoeff * LabelSample)

        return sum(KernelRegressionList)

    return [NWKernalRegressionResult(i,gamma,mode) for i in DataList]
    # return NWKernalRegressionResult(xInput,gamma)

def EmpiricRiskStatic(mode):

    def EmpiricRisk(NWKernelPredictList,LabelList,mode="FirstOrder"):

        assert mode in ["FirstOrder","SecondOrder"]
        ErrorList = list()
        for _,(NWKernelPredict,Label) in enumerate(zip(NWKernelPredictList,LabelList)):

            if mode == "FirstOrder":
                ErrorList.append(abs(NWKernelPredict - Label))
            else:
                ErrorList.append((NWKernelPredict - Label) ** 2)
        return sum(ErrorList) / len(ErrorList)

    GammaLimits = list(np.linspace(0, 0.5, 2000))
    EmpiricRiskList = list()
    EmpiricRiskListSecond = list()
    for GammaChoice in tqdm(GammaLimits):
        NWKernelPredictList = AlgorithmProcess(DataList,LabelList,GammaChoice,mode=mode)
        EmpiricRiskResult = EmpiricRisk(NWKernelPredictList, LabelList)
        EmpiricRiskList.append(EmpiricRiskResult)
        EmpiricRiskResultSecond = EmpiricRisk(NWKernelPredictList,LabelList,mode="SecondOrder")
        EmpiricRiskListSecond.append(EmpiricRiskResultSecond)

    plt.scatter(GammaLimits,EmpiricRiskList,s=2,c="tab:blue")
    plt.scatter(GammaLimits,EmpiricRiskListSecond,s=2,c="tab:orange")
    plt.savefig("EmpiricRisk.png")
    plt.show()

if __name__ == '__main__':
    Path = r""
    DataList, LabelList = DealTokenAndLabel(ReadXlsx(Path))
    EmpiricRiskStatic(mode="RBF")

关于使用$\text{Nadaraya-Watson}$核回归时，需要注意的点：

• 由于$\text{Nadaraya-Watson}$核回归自身是懒惰学习方法，因此，这里唯一的参数就是径向基核函数中描述的$\gamma$。而针对选择最优$\gamma$，这里使用的目标函数为经验风险$(\text{Empiric Risk})$：
  $$\mathcal{J}(\gamma )={\mathbb{E}}_{{\hat{\mathcal{P}}}_{data}}\left\{\mathcal{L}[f(x^{(i)};\gamma ),y^{(i)}]\right\}=\frac{1}{\mathcal{M}}\sum _{i=1}^{\mathcal{M}}\mathcal{L}[f(x^{(i)};\gamma ),y^{(i)}]$$
  其中$\mathcal{L}[f(x^{(i)};\gamma )]$表示关于$x^{(i)}$的预测结果$f(x^{(i)})$与真实标签$y^{(i)}$之间的差异性结果，也就是损失函数$\mathcal{L}(\cdot )$在$x^{(i)}$点处的结果。目标函数确定后，这里的处理方式是：

  • 在$\gamma$确定的情况下，将数据集${\hat{\mathcal{P}}}_{data}$中的每一个样本抽取出来，并使用剩余样本进行预测；
    值得注意的是：在抽取操作结束后，使用剩余样本做预测。因为如果被抽取样本依然保留在数据集内，那么在计算权重系数$\begin{array}{r}\frac{\kappa (x,x^{(i)})}{{\sum }_{j=1}^N\kappa (x,x^{(j)})}\end{array}$过程中，数据集内与被抽取样本相同的样本其权重必然占据极高比重，因为该项的分子必然是$1(e^0)$,从而该样本的预测结果会被数据集内相同的样本进行主导或者控制。个人实践踩过的坑~
  • 在所有样本均被遍历一次后，计算$\mathcal{J}(\gamma )$，记录并修改$\gamma$，执行下一次迭代。从而通过统计的方式得到$\gamma \in [0,1]$中的最优解。

• 关于损失函数$\mathcal{L}[f(x^{(i)};\gamma ),y^{(i)}]$，可以使用曼哈顿距离($1$阶)或者欧几里得距离($2$阶)对标签之间的差异性进行描述：
  无论$f(x^{(i)};\gamma )$还是$y^{(i)}$都是标量形式。因而没有使用范数进行表达。
  L [ f ( x ( i ) ; γ ) , y ( i ) ] = { ∣ f ( x ( i ) ; γ ) − y ( i ) ∣ ⇒ Manhattan Distance [ f ( x ( i ) ; γ ) − y ( i ) ] 2 ⇒ Euclidean Distance \mathcal L[f(x^{(i)};\gamma),y^{(i)}] = \begin{cases} \left|f(x^{(i)};\gamma) - y^{(i)} \right| \quad \Rightarrow \text{Manhattan Distance}\\ \quad \\ \left[f(x^{(i)};\gamma) - y^{(i)} \right]^2 \quad \Rightarrow \text{Euclidean Distance} \end{cases} L[f(x(i);γ),y(i)]=⎩ ⎨ ⎧​ ​f(x(i);γ)−y(i) ​⇒Manhattan Distance[f(x(i);γ)−y(i)]2⇒Euclidean Distance​

这里基于某数据集的回归任务，关于曼哈顿距离、欧式距离作为损失函数，$\mathcal{J}(\gamma )$与$\gamma$之间的关联关系表示如下：
其中横坐标表示$\gamma$的取值;纵坐标表示$\mathcal{J}(\gamma )$的映射结果。

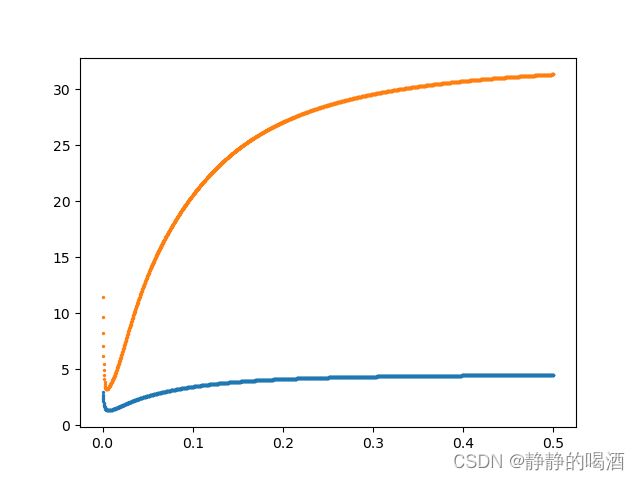
其中蓝色点形状表示曼哈顿距离作为损失函数的图像结果；而橙色点形状表示欧几里得距离作为损失函数的图像结果。从图中可以看出：在相似位置可以得到目标函数的最小值。
需要注意的是，两种函数无法相互比较，因为两者对应目标函数的值域不同。

个人想法

虽然通过统计的方式得到了$\gamma$的最优解，但它可能并不准。或者说：基于当前数据集${\hat{\mathcal{P}}}_{data}$，使用径向基核函数条件下的最准结果。其他优化的方式有：

• 核函数的选择；
  一般情况下,线性核函数本身是够用的。
• 扩充样本数据；
  • 在最早的概率与概率模型中介绍过，模型预测的不准的本质原因是预测模型与真实模型之间的差异性较大。而在$\text{Nadaraya-Watson}$核回归中，并没有涉及到具体模型。因而反馈的结果是:当前训练集所描述的概率分布与真实分布之间存在较大差距。
  • 由于真实分布是客观存在的，也就是说训练集的样本越多，分布就越稳定。体现在参数$\gamma$中的效果是:在样本数量较少时，不同的数据集对应的$\gamma$差异性可能很大(波动较大)；随着样本数量的增多，$\gamma$会逐渐趋于稳定。