“泰迪杯” 挑战赛 - 利用协同过滤与卷积神经网络为电视产品制订智能化营销推荐

目录

1. 问题重述
2. 模型假设
3. 数据预处理
   3.1 数据清洗
   3.1.1 数据缺失的分析和处理
   3.1.2 数据异常的分析和处理
   3.2 数据规约
4. 数据分析
   4.1 电视产品体系图
   4.2 收视用户体系图
   4.3 用户收视信息分析
   4.3.1 用户收视信息
   4.3.2 用户回看信息
   4.3.3 用户点播信息
   4.3.4 用户单片点播信息
   4.4 电视产品信息数据分析
   4.5 用户基本信息分析
   4.6 产品与用户画像
   4.7 评分体系
5. 推荐系统算法设计
   5.1 协同过滤算法
   5.1.1 基于用户的协同过滤算法
   5.1.2 基于电视产品的协同过滤算法
   5.1.3 电视产品的评分预测
   5.2 SVD
   5.3 KNNBaseline
   5.4 Normal Predictor
   5.5 Co-Clustering
   5.6 Text-CNN
   5.6.1 模型框架
   5.6.2 卷积层
   5.6.3 池化层
   5.6.4 模型训练
   5.6 推荐算法的融合
6. 推荐系统冷启动问题
   6.1 双重聚类算法
   6.2 用户冷启动问题
   6.3 电视产品冷启动问题
   6.4 用户的非个性化推荐方案
7. 实验设计与分析
   7.1 实验设计“泰迪杯”全国数据挖掘挑战赛论文报告
   7.2 推荐系统评测指标
   7.3 结果对比与分析
   7.3.1 问题一结果分析
   7.3.2 问题二结果分析
   参考文献

1. 问题重述

伴随着互联网技术的快速发展和应用拓展， “三网融合”（因特网、电信网、广播电视网） 为传统广播电视媒介带来了发展机遇，海量信息资源爆炸性增长，当前的世界正处在信息过载的时代。传统广电媒体作为大众信息的主要传播渠道，在面临着互联网媒体挑战的同时也在日趋深入地与之融合。电视互动性不断增强，观众的参与度大幅提升， 原本被动收视的用户开始更多有目的地“使用”电视所提供的资源与服务， 广播电视运营商可以与众多的家庭用户实现信息的实时交互， 使得全方位个性化的产品营销和有偿服务成为现实。然而随着影视节目资源数量的指数型增长，内容日趋多样，面对海量的节目资源，用户想找到自己需要的内容变得越来越困难。因此需要一种智能的、个性化的广电节目推荐系统，帮助用户在信息的海洋中发现自己需要的电视节目产品，同时也使内容的生产、传播更具有目的性和精准性，从而实现价值的最大化。

智能推荐技术应用于电子商务领域起步较早，现已经比较成熟，但是在广电领域应用智能推荐与之相比有很多不同之处，数据集不同，算法的表现也会存在差异。 Joonseok等对影响个性化推荐算法精准度的因素进行了分析，研究表明用户数量、产品数量以及评分矩阵的密集度会影响算法的精准度。电子商务中推荐的商品特征多为结构性数据，比较容易获取并且可以准确描述，例如用户喜欢的品牌、颜色、款式等。广电系统中的用户收视信息特征较难提取，非结构化的数据处理比较困难，数据容量大且相似性度量不好定义。此外用户分层差距较大，收视用户的反馈信息获取不便，视频资源的属性特征无法直观地表达用户的兴趣特征等也增大了广电业务推荐的难度。

本研究的主要内容为：结合某广电网络运营公司给出的部分用户的观看记录信息数据和运营公司的产品信息数据，利用数据挖掘的方法解决以下两方面问题。
  1、 产品的精准营销推荐。根据已知的用户观看的收视记录信息数据，采用数据挖掘的方法分析用户的收视偏好，并给出电视节目产品的营销推荐方案。
  2、 针对用户的收视信息，对相似偏好的用户通过用户画像方式标签并分类，根据产品标签对电视节目产品进行分类打包， 并给出营销推荐方案。

2. 模型假设

针对实际的电视产品营销推荐系统而言，为了获得精准地营销推荐方案，我们必须
做出如下合理的假设：
1、假设所给的数据集是完备可靠的；
2、假设网络爬虫提取的数据是正确可靠的；
3、假设用户对于电视节目的观看时长与其对该节目的喜爱度成正相关关系；
4、假设电视机的机顶盒所记录时长均为用户的有效观看时间；
5、假设所有用户在推荐方案给出后的一段时间内正常收视电视节目；
6、假设所有电视产品的属性均隶属于我们所设计的产品体系表。

3. 数据预处理

针对题目中所给的原始数据而言，原始数据中存在着大量的冗余信息、不一致信息、非结构化数据和有异常的数据，这将会严重的影响数据挖掘和建模的执行效率，甚至可能会导致数据挖掘的结果出现偏差，因此，必须先对给定的原始数据进行预处理操作，提高数据集的质量，并使得数据能够更好地适应我们的挖掘算法和数学模型。

3.1 数据清洗

数据清洗主要是删除原始数据集中的无关数据、重复数据和有噪声的数据，筛选过滤掉与电视产品推荐主题无关的数据， 并且合理地处理缺失数据和异常数据。

3.1.1 数据缺失的分析和处理

数据的缺失主要包括记录的缺失和记录中某个字段信息的缺失，两者都会造成分析结果的不准确, 使得数据挖掘模型所表现出的不确定性更加显著，模型中蕴含的规律更难把握，导致不可靠的输出。首先，我们利用 Pandas 对附件三中所有的用户信息，共计1329 条记录，进行统计分析。其次，针对附件一中用户的历史收视行为、回看行为和单片点播行为进行正则匹配查找，可以得到含有缺失值的属性的个数，以及每个属性的未缺失值、缺失值与缺失率等，我们发现有 274 个用户不存在任何收视和点播信息， 部分无任何记录的用户见表 3-1 所示。

表 3-1 部分无历史行为用户表

3.1.2 数据异常的分析和处理

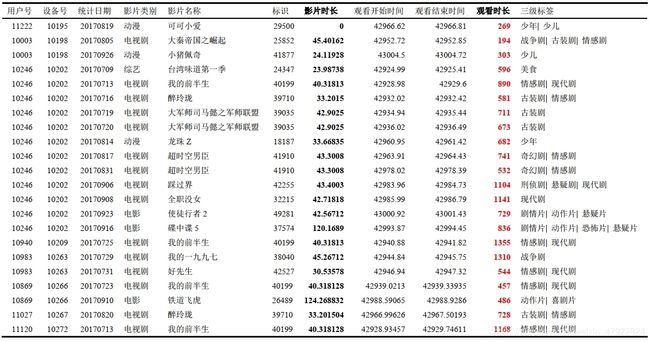
异常值是指样本中的个别值，其数值明显偏离其余的观测值。异常值也称为离群点，异常值的分析也称为离群点分析。异常值分析是检验数据是否录入错误以及是否含有不合常理的数据。忽视异常值的存在是十分危险的，不加剔除地把异常值包括进电视产品推荐数据挖掘的计算分析过程中，对结果会带来不良影响；针对用户收视信息和电视产品信息可以先做一个描述性统计， 然后在经过正则化匹配查找发现多个电视产品节目名称包含冗余的无效信息见表 3-2 所示。 由于题目要求对附件二中的产品进行推荐，因此在对用户点播信息进行处理时，对于未出现在附件二中的产品，我们进行了过滤。充分考虑到电视产品在播放期间的插播广告时间，我们在提取有效数据时，通过相关资料查阅，将广告时长合理地设置为 10 分钟，即过滤掉用户实际观看时长大于附加广告时长后的影片时长的异常值，部分用户观看时长异常值见表 3-3 中粗体所示。

表 3-2 电视节目产品冗余信息处理表

表 3-3 用户观看时长异常值表

3.2 数据规约

在对用户的收视和点播行为的大数据集上进行复杂的数据分析和挖掘将需要非常多的计算时间，数据规约能够产生更小的但保持原始数据完整性的新数据集，提高推荐系统的准确性，大幅度缩减数据挖掘所需的时间，有效降低存储数据的成本。因此，在规约之后的数据集上进行分析和挖掘将会更加有效率。

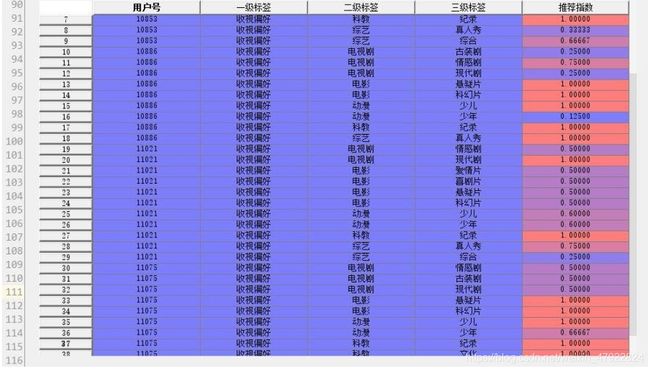
譬如，在以用户为粒度，对附件一中的收视信息和点播信息进行统计分析时发现, 大量用户针对某一电视节目存在集数观看或重复观看信息，我们为了后期的数据挖掘处理方便，将存在多集数观看的电视剧或者别的电视产品节目均归类为 1 条有效的电视产品节目记录，并针对该用户对电视节目的观看时长和观看次数进行求和统计。 附件一中用户单片点播信息共计 38010 条记录，经过数据规约处理后，共计 3627 条有效信息，包括 352 个用户对 527 种电视节目产品的点播记录。 同样对附件二中的电视节目产品进行规约化处理，原附件二中电视节目产品共计 18480 个, 对电视节目产品归一化后得到共计 2123 个电视节目产品。

具体处理方式以附件一中用户号为 11087 的用户的点播行为举例说明，原始数据中共 323 条该用户的点播行为信息，经过规约与标签处理后，压缩为 16 条有效信息，如图 3-1 中的数据所示，该数据格式可以为接下来的数据挖掘工作提供更加有效的信息。

图 3-1 用户点播行为规约处理示意图

4. 数据分析

4.1 电视产品体系图

根据规约处理后的数据集，我们将电视产品信息进行分类，产品的基本特征主要分为电视剧、电影、综艺、少儿、新闻、科教和体育，共 7 大类；电视产品的适用人群主要分为老人、儿童、青年、男性和女性，共 5 类。 详细的产品体系如图 4-1 所示。

图 4-1 电视产品体系图

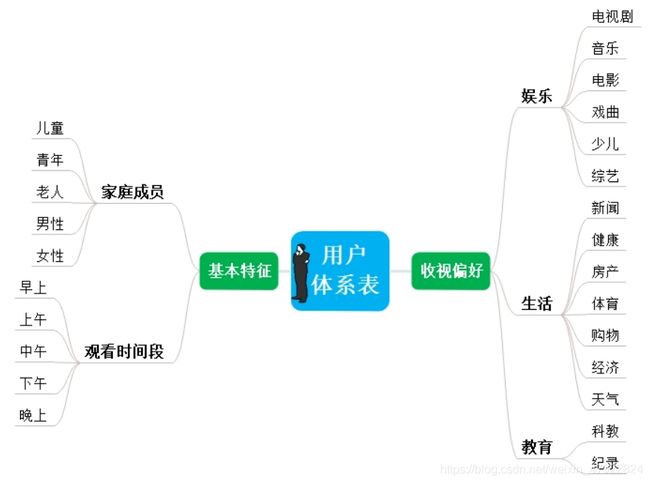
4.2 收视用户体系图

根据规约处理后的数据集， 我们通过附件一中的用户的收视信息， 建立了收视用户体系表。 该收视用户体系主要分为基本特征和收视偏好两大类。 其中， 用户的收视偏好主要分为娱乐、生活和教育； 基本特征主要划分为家庭成员和观看时间段。 详细的收视用户体系如图4-2所示。

图 4-2 收视用户体系图

4.3 用户收视信息分析

4.3.1 用户收视信息

针对所提供的用户收视信息表进行分析，该表提供的信息一共包含六项，分别为机顶盒设备号，统计日期，频道号，频道名和收看开始与结束时间，共计 361963 条记录。

图 4-3 用户收视信息三维透视图

图 4-3 中横轴（ X 轴）表示用户所观看的电视频道，纵轴（Y 轴）表示相应的用户号，竖轴（ Z 轴）表示用户的观看电视节目的时长，不同的颜色分别表示不同的用户。总体而言，此图表示用户观看电视频道的总观看时长。图 4-3 中的用户和频道只是节选了附件一的“用户收视信息”中几个具有代表性的用户和频道作为示例， 柱形图的柱子越高， 就表示用户观看的时间越长， 从图中可以直观地看出“翡翠台”、 “湖南卫视”、 “中央少儿”和“优漫卡通”的总体收视时长都偏高， 可以反映出这几个电视频道比较受广大收视用户的青睐。

4.3.2 用户回看信息

图 4-4 用户回看信息三维透视图

图 4-4 的横轴（X 轴）表示被用户回看的电视频道，其纵轴（ Y 轴）表示相应的用户号，竖轴（ Z 轴）表示用户的观看电视频道的总时长，不同的颜色代表不同的用户。此图表示的是用户的回看信息，即不同的用户回看不同的频道时所花费的时间。由于附件一中“用户回看信息”的用户较多， 同时电视的频道号也较多不便全部列举， 因此， 在此只选取了几个具有代表性的用户收视信息进行分析。 从图中可以直观看出， 对于“东方卫视”、 “浙江卫视”、 “湖南卫视”和“江苏卫视”等几个电视频道用户回看较为突出， 这些频道备受用户的青睐，可以考虑作为热门的电视节目频道。

4.3.3 用户点播信息

为了针对性地分析付费用户的电视节目点播行为，设计出较为精确的电视产品推荐营销方案， 我们对“用户点播信息”中的不同用户的付费状况进行了分析。 表 4-1 中列举了附件一中的“用户点播信息”中的所有用户在电视点播上的消费总金额， 即每个用户在点播电视节目方面所花费的金额， 总消费金额大于 100 的用户在表中用粗体显示，总消费金额大于 50 小于 100 的用户在表中以加粗带下划线显示。 表 4-1 中将总金额从高到低依次递减排序，排名越靠前的用户，其消费水平也就越高，即更有意愿对点播的电视产品付费，当进行个性化推荐的时候可以重点关注此类用户。

表 4-1 用户点播付费总金额表

4.3.4 用户单片点播信息

图 4-5 用户单片点播信息三维透视图

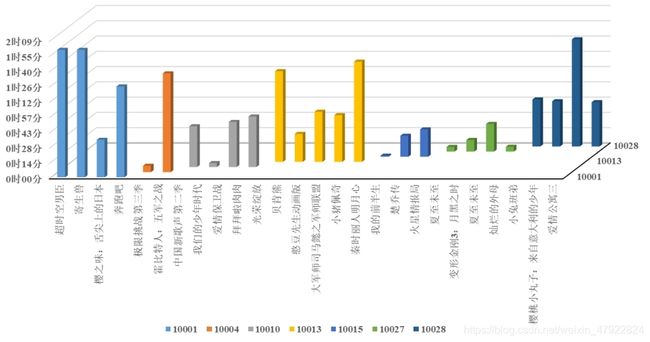
图4-5中展示了附件一中的用户单片点播信息，图4-5中横轴（ X轴）表示用的点播的电视节目，纵轴（Y轴）表示相应的用户号，竖轴（ Z轴）表示用户对于电视节目的观看时长，不同的颜色用于区分不同的用户，由于数据表中观看信息记录较多，因此，我们只抽取了其中一部分具有代表性的用户点播信息进行示例展示。如图4-5所示，图中的柱子越高， 就代表用户的收看时间越长， 例如对于10001用户而言， 其观看“超时空男臣”、“寄生兽”、 “奔跑吧”时长相对较长； 用户10013观看“贝肯熊”和“秦时丽人明月心”的观看时长较长； 用户10028观看“樱桃小丸子”的收视时长偏高等。 这些细节信息的抽取非常有必要，可为我们对用户画像提供可识别的特征，精准设计电视产品推荐方案提供支撑。

4.4 电视产品信息数据分析

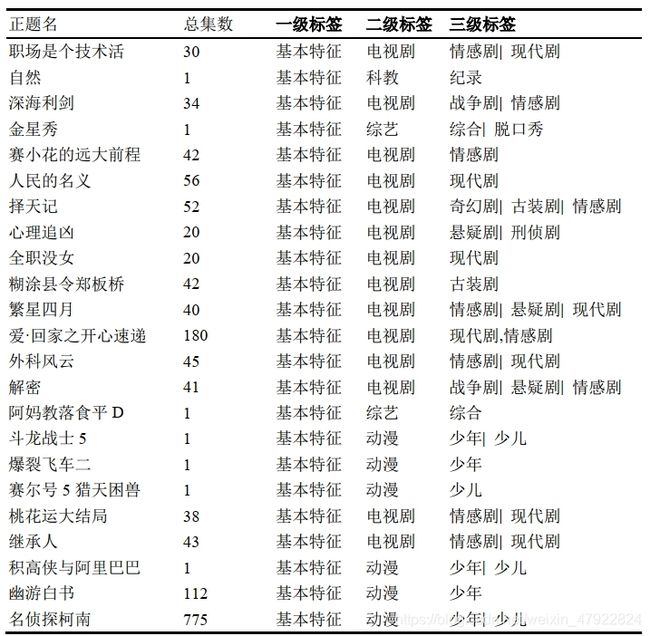
本节针对给出的“附件二： 电视产品信息数据”表进行数据预处理， 该表包含标识、正题名、创建日期、导演、演员、出品年代、内容描述、总集数、分类名称、连续剧分类、声道语种和地区参数共12类信息，共计2123条记录，我们针对电视产品营销推荐系统， 通过特征抽取的方法， 获得2类关键特征。 我们对“正题名”、 “总集数”两类特征进行“泰迪杯”全国数据挖掘挑战赛论文报告分析， 得出用户评分依赖集数， 同时根据“正题名”爬取到一二三级标签， 可以通过标签对产品进行分类，具体结果见表4-2所示。例如表中名侦探柯南， 775集，我们通过网络爬虫获得的一二三级标签分别为“基本特征”、 “动漫”和“少年|少儿”。

表 4-2 电视节目产品标签表

4.5 用户基本信息分析

本节针对给出的“附件三： 用户基本信息”表进行数据预处理， 该表包含用户号、 业务品牌、用户状态、状态改变时间、预存款、套餐、销售品、资费、入网时间、销售品生效时间、销售品失效时间、机顶盒编号共12类信息，共计1329条记录，我们针对电视产品营销推荐系统， 通过特征抽取的方法， 获得“用户号”、 “设备号”两类关键特征， 通过这两类关键特征编写出数据字典， 见表4-3所示。 例如表中用户号为“11183”的用户，“泰迪杯”全国数据挖掘挑战赛论文报告其机顶盒编号为“11284”， 这样就能够把用户的用户号和机顶盒号进行关联， 为其它附件进一步的数据分析工作做支撑。

表 4-3 用户号-机顶盒编号匹配表

4.6 产品与用户画像

用户画像是根据用户人口统计学信息、社交关系、偏好习惯和消费行为等信息而抽象出来的标签化画像。 构建用户画像的核心工作即是给用户贴“标签”， 而标签中部分是根据用户的行为数据直接得到，部分是通过一系列算法或规则挖掘得到。对产品和用户进行画像可以实现对产品和用户的分类，网络爬虫技术则是解决产品及用户画像的一个有效手段。网络爬虫也称网络蜘蛛，或网络机器人。它为搜索引擎从万维网上下载网页，并沿着网页的相关链接在Web中采集资源，是一个功能很强的网页自动抓取程序，也是搜索引擎的重要组成部件，它的处理能力往往决定了整个搜索引擎的性能及扩展能力等。

针对清洗后的附件一，我们获取了所有收视频道24小时各时段的播放节目类型信息，利用该信息及用户体系表对收视信息表中的所有用户贴标签，确定各用户的收视偏好及家庭成员，实现用户分组。针对清洗后的附件二，我们采用网络爬虫技术和产品体系表对附件二中的产品贴标签，利用Python及第三方库Beautiful Soup4 v4.6.0对百度视频进行电视节目产品的信息抓取，从而实现对产品的分类打包。通过对附件一及附件二中产品及用户画像，不仅解决了用户分组及产品打包要求，同时可以为用户及产品的冷启动问题提供有效数据信息支撑。

4.7 评分体系

我们用的是隐性评分数据预处理系统主要对数据进行筛选和打分，对节目推荐系统输出节目评分矩阵。目前用户对于节目的评分值常用方法有两种： (1)显式评分：用户主动提交自己对于节目的喜好，一般是在注册时进行问卷式调研或者在观看之后让用户填写评，因为很多用户并不习惯主动评分，还有些用户因为抗拒感而胡乱评分，这些因素都会导致错误的推荐结果。 (2)隐式评分：根据收集用户已经收看的节目行为数据进行建模，得到用户对于节目的喜爱程度预测。
针对所给数据分析后可知，电视用户对于节目评分的影响因素主要以下几点： (a)电视观看时间，这是主要的影响因素，观看时间很大程度代表了用户的喜好程度。当然这里的时间必须归一化处理，最终采用节目观看时间占总时间的比例。 (b)节目观看频率，观看频率是最重要影响因素，观看频率可以一定程度上体现出用户对该产品的喜好程度。

针对需要提供附件二中产品的推荐方案的要求，我们在对附件一中用户点播信息数据进行处理时，主要考虑包含附件二中产品的有效点播信息，因为附件一中点播的电视节目产品信息均来自附件二。本文采用隐式评分系统，根据用户点播信息可知，电视产品主要分为电视剧、电影、综艺、少儿和科教五大类别。不同的电视产品点播频率受产品总集数、是否正在热播等因素的影响。定义$U_{i,j}$ 为用户 $i$ 对电视节目产品 $j$ 的观看时长，观看频率为$\omega$，本文采用基于电视节目的观看频率与平均观看时长作为得分的测度指标更具有客观性。 我们根据用户$i$平均观看时长$U_h$与电视产品节目j时长$T_j$的比值${\alpha }_{i,j}$ ，将收视用户对于不同电视节目产品的评分划分为5个分数等级，记 $Score(i,j)$ 为用户$i$ 对电视节目产品 $j$ 的评分， 收视用户的隐性评分公式见(4-1)和(4-2)所示：
$${\alpha }_{i,j}=\frac{1}{\omega T_j}\sum _{\sigma =1}^{\omega }\bigcup _{i,j}^{sigma}$$

(4-1)

$$Scor{e}_{i,j}=\{\begin{array}{l}1,0<{\alpha }_{i,j}\le 0.2\\ 2,0.2<{\alpha }_{i,j}\le 0.4\\ 3,0.4<{\alpha }_{i,j}\le 0.6\\ 4,0.6<{\alpha }_{i,j}\le 0.8\\ 5,0.8<{\alpha }_{i,j}\le 1.0\end{array}$$

(4-2)

5. 推荐系统算法设计

针对电视产品的推荐系统，其用户数据经过清洗之后可以整理成一个User-Item标准矩阵。矩阵中每一行代表一个用户，而每一列则代表一个电视节目。若用户对电视节目有过评分，则矩阵中处在用户对应的行与电视节目对应的列交叉的位置表示用户对电视节目的评分值，相应的该User-Item矩阵被称为评分矩阵。

图5-1 用户-电视产品评分散点示意图

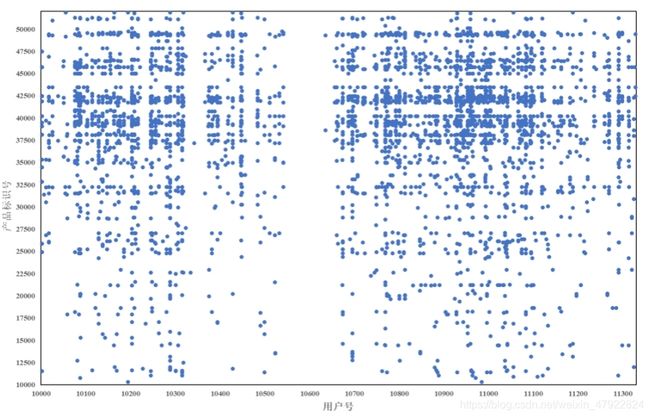
图5-1中的散点代表有相应用户对电视产品进行评分，根据图5-1可以明显看出评分矩阵的数据是非常稀疏的，图中大量空白处表示用户还没有对电视节目做出评价，而推荐系统最终的目标就是对于任意一个用户，预测出所有未评分电视节目的分值，并按分值从高到低的顺序将对应的电视节目推荐给用户。

5.1 协同过滤算法

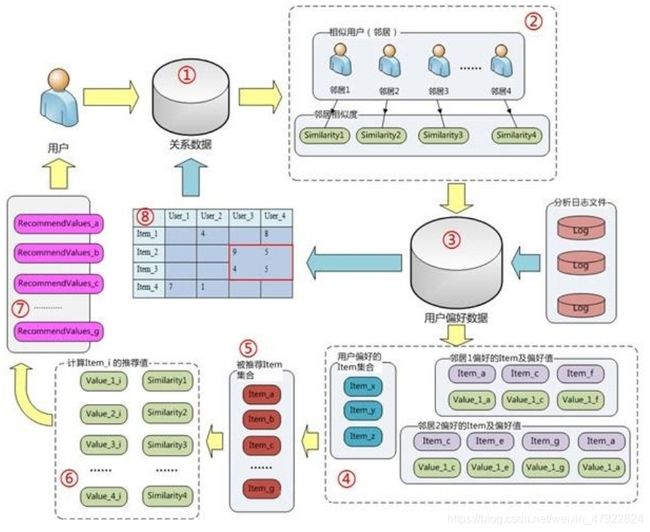
推荐系统应用数据分析技术，找出用户最可能喜欢的东西推荐给用户，现在很多电子商务网站都有这个应用。 Goldberg 等[1]于 1992 年提出了协同过滤(Collaborative Filtering, CF)的概念，最初应用在 TapestrySystem 上过滤对用户有用的电子邮件。 经过近 20 年的发展，协同过滤已成为智能推荐领域的重要算法。基于协同过滤的推荐系统，主要依据的是用户或者项目之间的相似性，通过将用户和其他用户的数据进行对比来实现推荐的。基于协同过滤的推荐系统用可以分为两类：（ 1）基于用户的协同过滤(Userbased CF)推荐系统，主要依据的是用户的历史行为数据挖掘获取知识，并对这些数据进行度量和打分，再根据目标用户的偏好即用户与用户之间的相似性，找到与目标用户兴趣相似的用户群体并将该群体感兴趣的内容推荐给目标用户，为目标用户提供定制化服务;（ 2）基于项目的协同过滤(Item-based CF)推荐系统，主要依据的是项与项之间的相似性，计算目标产品与用户喜欢的或已购买的产品的相似度，将相似度较高的产品推荐给用户。 协同过滤算法流程示意图见图 5-2 所示。

图 5-2 协同过滤算法流程示意图

5.1.1 基于用户的协同过滤算法

对于一个特定用户 $x$，首先找到与其相似的一个用户集，这个相似是通过它们的评分(Rating)来判定的，用户的 Likes 和 Dislikes 越相似，他们就越相似。然后推荐这些相似用户集喜欢的 Items 并且预测 x 评分最高的 Items 给用户 $x$。基于用户的推荐算法和基于产品的推荐算法涉及到用户/产品之间的相似度的计算，计算用户间以及电视产品间的相似度选用皮尔逊相关系数方法(Pearson Correlation)来度量用户/产品间的相似度。相比于其他的相关度评价指标而言，对于不规范的评分数据皮尔逊相关度评价能够给出更好的结果。皮尔逊相关系数的计算公式如 5-1 所示，结果是一个在-1 与 1 之间的系数。该系数用来说明两个用户间联系的强弱程度（其中， 0.8-1.0 极强相关； 0.6-0.8 强相关；0.4-0.6 中等程度相关； 0.2-0.4 弱相关； 0.0-0.2 极弱相关或无相关）。
$${\rho }_{preson}(i,j)=\frac{\sum x_i{y}_i-n\overline{xy}}{(n-1)S_x{S}_y}-\frac{n\sum x_i{y}_i-\sum x_i\sum y_i}{\sqrt{n\sum {x_i}^2-(\sum x_i{)}^2}\sqrt{n{\sum y_i}^2-(\sum y_i{)}^2}}$$

(5-1)

首先基于用户对电视产品的偏好找到相邻邻居用户， 然后再将邻居用户喜欢的电视产品推荐给当前用户。计算上，就是将一个用户对所有电视产品的偏好作为一个向量来计算用户之间的相似度，找到 k 邻居后，根据邻居的相似度权重以及他们对电视产品的偏好，预测当前用户没有偏好的未涉及的电视产品，计算得到一个排序的电视产品列表作为推荐，基于用户的协同过滤见图 5-3 所示。

图 5-3 基于用户的协同过滤示意图

但是 User-based CF 算法对于电视节目推荐存在两个问题：（1）数据稀疏性。针对成百上千个不同电视产品的推荐系统一般有非常多的电视节目，收视用户可能观看的其中很少一部分电视节目，不同收视用户之间付费的电视产品重叠性较低，导致算法无法精准找到收视用户的邻居，即偏好相似的用户。（ 2）算法扩展性。最近邻居算法的计算量随着收视用户和电视节目数量的增加而增加，不适合数据量大的情况使用。

5.1.2 基于电视产品的协同过滤算法

基于电视产品的协同过滤的原理和基于用户的协同过滤类似，只是在计算邻居时采用各种电视产品进行计算，而不是从用户的角度，即基于用户对产品的偏好找到相似的电视产品，然后根据用户的历史偏好，推荐相似的电视产品给用户，见图 5-4 所示。从计算的角度看，就是将所有用户对某个电视产品的偏好作为一个向量来计算各种电视产品之间的相似度，得到电视产品的相似产品后，根据用户历史的偏好预测当前用户还没有表示偏好的电视产品，计算得到一个排序的产品列表作为推荐。

图 5-4 基于电视产品的协同过滤示意图

从表 5-1 中可知， User CF 更适合用于个性化新闻推荐，个性化新闻推荐更加强调抓住新闻热点，热门程度和时效性是个性化新闻推荐的重点。 Item CF 更适合用于在图书、电子商务和电视产品方面的个性化的推荐，比如亚马逊、豆瓣、 Netflix 和广电产品打包推荐中， Item CF 则能极大地发挥优势。

表 5-1 User CF 和 Item CF 优缺点的对比表

5.1.3 电视产品的评分预测

根据之前基于Item CF计算好的电视产品之间的相似度，对未打分的电视产品进行预测标定，本节中提出两种方法可以采用：（ 1）加权求和。针对在评分体系中我们对收视用户$u$给定打分的电视节目的分数进行加权求和，权值为各个电视节目与节目之间的相似度，然后对所有的电视节目的相似度之和求平均，计算得到收视用户$u$对电视产品$i$的预测评分，相应的计算公式如5-2所示：
$$P_{ui}=\frac{{\sum }_{allsimilaritems}S(i,N)\ast Score(u,N)}{{\sum }_{allsimilaritems}|S(i,N)|}$$

(5-2)

其中， $S(i,N)$为电视产品i与电视产品N的相似度， $Score(i,N)$ 为我们设定的评分体系下收视用户$u$对电视产品$N$的评分。

（ 2）回归预测。该方法和方案（ 1）的加权求和的方法类似，但回归的方法不直接使用相似电视产品N的打分值$Score(u,N)$ ，因为用余弦法或Pearson关联法计算相似度时存在一个误区，即两个评分向量可能相距比较远（欧氏距离），但有可能有很高的相似度。如果两个用户都喜欢某个电视产品，因为评分标准选取不同，他们的欧式距离可能比较远，但他们应该有较高的相似度。在这种情况下在根据收视用户原始的相似电视节目评分值进行计算会造成欠佳的预测结果。因此可通过用线性回归的方式重新估算一个新的值$Score(u,N)$，运用上面同样的方法进行预测,计算 $Score(u,N)$ 的方法如5-3所示：

$$S(N{)}^{\ast }=\alpha \overline{S}(i)+\beta +ϵ$$

(5-3)

5.2 SVD

针对矩阵分解技术，分为有特征值分解(Eigende Composition)与奇异值分解(Singular Value Decomposition, SVD）两种方法。对于特征值分解，由于其只能作用于方阵，因此并不适合分解推荐系统中评分矩阵的情况，因此采用SVD方法。对于奇异值分解，其具体描述为：一个 $m\times n$的$M$矩阵，一定存在一个奇异值分解$M=U\sum V^T$ ，其中$U$是 $m\times n$的正交矩阵， $V$是 $n\times n$的正交矩阵， $\sum$是$m\times m$ 的对角阵， SVD方法非常适合对推荐系统中的评分矩阵进行特征分解。 SVD中对角阵Σ还有一个特殊的性质， 它的所有元素都非负，且依次减小。这个减小也特别快，在很多情况下，前10%的和就占了全部元素之和的99%以上，这就是说我们可以使用最大的$k$个值和对应大小的$U$、 $V$矩阵来近似描述原始的评分矩阵。 因此， 针对原始的评分矩阵M做奇异值分解， 得到$U$、 $V$及$\Sigma$， 取$\Sigma$中较大的k类作为隐含特征， 则此时M被分解成$U$、 $\Sigma$和$V$， 接下来就可以直接使用矩阵乘法来完成对原始评分矩阵的填充。对于数据稀疏的矩阵而言，在推荐系统中可以考虑将原始评分矩阵$M$满秩分解成两个矩阵$P$和$Q$，其中， $P_{uk}$ 可以看作是用户$u$对电影的隐藏特质$y$的热衷程度，而Qki 可以看作是特质$k$在电影$i$中的体现程度。同时考察原始评分矩阵中有评分的项分解结果是否准确，而判别标准则是均方差，那么上述模型的评分预测公式为：
$$M_{ui}=\sum _{k=1}^k{P}_{uk}{Q}_{ki}$$

(5-4)

其中， $P$和$Q$分别对应了电影和用户在各个隐藏特质上的特征向量。对于所有机器学习算法而言，过拟合一直是需要重视的一个问题，因此我们在SSE中加入正则化项，这样可以在训练中防止过拟合。因此整个评分矩阵总的损失可定义为：
$$\begin{gathered} SSE={\sum _{ui}{E}_{ui}}^2=\sum _{ui}(M_{ui}-{\hat{M}}_{ui})+\lambda \sum _u{P}_u^2+\lambda \sum _i{Q}_i^2 \\ =\sum _{ui}(M_{ui}-\sum _{k=1}^k{P}_{uk}{Q}_{ki}{)}^2+\lambda \sum _u{P}_u^2+\lambda \sum _i{Q}_i^2 \end{gathered}$$

(5-5)

因此，只要尽可能地使式(5-5)的损失SSE最小化，就能够以最小的扰动完成对原始评分矩阵的分解，在这之后只需要用计算 $\hat{M}$ 的方式来完成对原始评分矩阵的填充即可。由公式可知SSE是关于$P$和$Q$的多元函数，当随机选定$U$和$I$之后，需要枚举所有的$k$，并且对 $P_{uk}$ 和$Q_{ki}$ 通过链式法则求偏导数，见式(5-6)和(5-7)所示。

$$\frac{\delta }{\delta P_{uk}}{E_{ui}}^2=2E_{ui}\frac{\delta E_{ui}}{\delta P_{uk}}=-2E_{ui}{Q}_{uk}+2\delta P_u$$

(5-6)

$$\frac{\delta }{\delta Q_{ki}}{E_{ui}}^2=2E_{ui}\frac{\delta E_{ui}}{\delta Q_{ki}}=-2E_{ui}{P}_{uk}+2Q_I$$

(5-7)

在推荐系统运行过程中，为了$P$和$Q$中所有的值都能得到更新，可以采用在线学习的
方式选择评分矩阵中有分数的点对应的$U$、 $I$来进行迭代，此处选取SGD随机梯度下降法
对其进行训练，我们也给出了相应详细计算过程。

然而实际上，有很多性质是用户或者电视节目所独有的。例如，某个用户非常严苛，不论对什么电视节目都给出的分数都很低，这仅仅与用户自身有关。又比如某部电影非常精彩，所有用户都会给出较高的分数，这也仅仅与电影自身有关。因此，只通过用户与电影之间的联系来预测评分是不合理的，同时也需要考虑到用户和电影自身的属性。因此， 评分预测的公式也需要进行修正。 不妨设整个评分矩阵的平均分为σ， 用户$U$和电影$I$的偏置分别$b_u$和$b_i$，那么此时的评分计算方法就更新见式(5-8)所示：

$${\hat{M}}_{ui}=\sigma +b_u+b_i+\sum _{k=1}^k{P}_{uk}Qki$$

(5-8)

同时，误差E除了由于$\hat{M}$计算方式带来的变化之外，也同样需要加入$U$和$I$偏置的正则项，因此最终的误差函数修整成如下所示：

$$SSE=\sum _{ui}{E}_{ui}^2=\sum _{ui}(M_{ui}-\widehat{M_{ui}}{)}^2+\lambda \sum _u{P}_u^2+\lambda \sum _u{Q}_i^2+\lambda \sum b_u^2+\lambda \sum _i{b}_i^2$$

(5-9)

实际上，对于用户点击查看电影这个行为，排除误操作的情况，在其余的情况下可以认为用户对电影的描述，例如内容或者画面描述等所吸引。这些信息称之为隐式反馈。事实上一个推荐系统中有明确评分的数据是很少的，这类隐式数据才占了绝大部分。预测的精度不仅要考虑显示的反馈，也需要考虑一些隐反馈。可以发现，在我们上面的算法当中，并没有运用到这部分数据。某个用户对某个电影进行了评分，那么说明他看过这部电影，那么这样的行为事实上蕴含了一定的信息，因此我们可以这样来理解问题：评分的行为从侧面反映了用户的喜好，可以将这样的反映通过隐式参数的形式体现在模型中，从而得到一个更为精细的模型SVD++。于是对于评分的方法，我们可以在显式兴趣和偏置的基础上再添加隐式兴趣，即可以建模得到式(5-10)：

$$\widehat{M_{ui}}=\sigma +b_u+b_i+\sum _{k=1}^k（P_{uk}+\frac{1}{\sqrt{|N(u)|}}\sum _{j\in N(u)}{y}_{jk}）Q_{kj}$$

(5-10)

其中，$N(u)$表示为用户$u$提供了隐式反馈的电影的集合，$yj$为隐藏的“评价了电影$j$”反映出的个人喜好偏置。因此可以通过SVD++算法进行推荐，此时的损失函数也同样需要加上隐式兴趣的正则项，即
$$SSE=\sum _{ui}{E}_{ui}^2=\sum _{ui}(M_{ui}-\widehat{M_{ui}}{)}^2+\lambda \sum _u{P}_u^2+\lambda \sum _u{Q}_i^2+\lambda \sum b_u^2+\lambda \sum _i{b}_i^2+\lambda \sum _{j\in N(u)}{y}_j^2$$

(5-11)

在实际的推荐中，我们还可以将原始的SVD++得到的结果与对偶算法得到的结果进行融合，通过不同的梯度下降策略进行求解，使得推荐的预测更加准确。

5.3 KNNBaseline

基于用户的协同过滤算法是一种基于内存的协同过滤算法，利用其它用户的评分来预测目标用户的评分，其假设是偏好相似的用户对项的评分也相似。目标用户的未知评分的项可以利用与该用户相似的一些用户的对应项的评分来预测。

邻居的定义是基于用户之间的相似性，或者给定数目的最相似用户（如k最近邻居）或者相似性超过一定阀值的所有用户。对于协同过滤算法最常用的相似性度量方法是皮尔逊相关系数(Pearson Correlation)、余弦相关系数(Cosine Similarity)和改进余弦相关系数(Adjust Cosine Similarity)，详细计算公式如下所示：

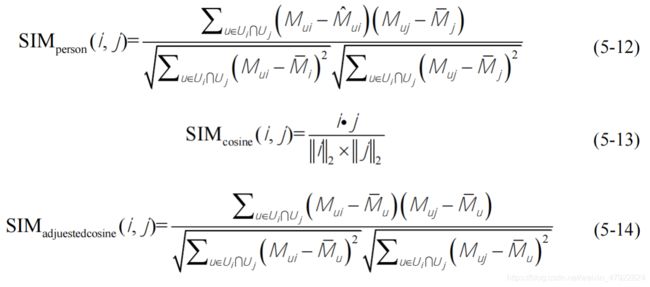
首先需要估算用户$u$对于收视节目$i$的评分：
1、找出用户$u$评价过的所有广电收视产品，采用以上相似度公式计算出和i最相似的前$k$个产品，这$k$个“邻居”记作$S^k(i,u)$。 通过对这$k$个产品的用户$u$的评分的加权值作为$u$对$i$评分的估计值，即$\widehat{M_{ui}}=\frac{{\sum }_{j\in S}S(i,j)M_{uj}}{{\sum }_{j\in S}|S(i,j)|}$,具体计算步骤如下所示：

KNNBaseline 是在 KNNWithMeans 基础上，采用Baseline的值来替换均值，详细的计算公式如5-15和5-16所示：

$$\widehat{M_{ui}}=b_{ui}+\frac{{\sum }_{V\in N_i^k(u)}sim(u,v)(M_{ui}-b_{vi})}{{\sum }_{V\in N_i^k(u)}sim(u,v)}$$

(5-15)

$$\widehat{M_{ui}}=b_{ui}+\frac{{\sum }_{j\in N_u^k(u)}sim(i,j)(M_{uj}-b_{uj})}{{\sum }_{V\in N_u^k(u)}sim(i,j)}$$

(5-16)

5.4 Normal Predictor

Normal Predictor 预测方法是假设评分数据来自于一个正态分布，针对给定一组样本
$x_1,x_2,....,x_n$进行建模，假设它们来自于高斯分布$N(\mu ,\sigma )$ ，通过样本估计参数
$\mu ,\sigma$ 。高斯分布的概率密度函数$f(x)={\frac{1}{\sqrt{2\pi }\sigma }}^{e^{-}\frac{(x-\mu {)}^2}{2{\sigma }^2}}$, 将样本 $x_1,x_2,....,x_n$值带入可得：

$$L(x)=\prod _{i=1}^n{\frac{1}{\sqrt{2\pi }\sigma }}^{e^{-}\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$

(5-17)

再将$L(x)$取对数后进行化简：
$$\begin{gathered} L(x)=log\prod _{i=1}^n{\frac{1}{\sqrt{2\pi }\sigma }}^{e^{-}\frac{(x-\mu {)}^2}{2{\sigma }^2}}=(\sum _{i}log\frac{1}{\sqrt{2\pi }\sigma })+(\sum _i-\frac{(x_i-\mu {)}^2}{2{\sigma }^2}) \\ =-\frac{n}{2}log(2\pi {\sigma }^2)-\frac{1}{2{\sigma }^2}\sum _i(x_i-{\mu }^2) \end{gathered}$$

(5-18)

最后对$L(x)$再求导，就能得到估计的参数$\mu ,\sigma$。

$$\{\begin{array}{l}\mu =\frac{1}{n}{\sum }_i{x}_i\\ {\sigma }^2=\frac{1}{n}{\sum }_{i(x_i-\mu {)}^2}\end{array}$$

(5-19)

5.5 Co-Clustering

随着广电服务中收视用户和电视节目项的数量不断增加，为了产生精确的推荐，保证推荐系统的实时性要求，产生了基于模型的协同过滤算法，主要思想是通过已知的评分数据来确定模型中的参数，用参数确定的模型来预测未知的评分数据。最常见的模型有贝叶斯(Bayesian)模型、聚类(Clustering)模型、回归(Regression)模型和隐含语义(Latent Semantic)模型等。其中聚类模型的主要优势在于降低数据维度，提高计算效率，数据之间的簇信息在一定程度上解决了数据稀疏性和数据动态性的问题。目前对协同过滤中应用聚类方法的研究比较多，通常采用的有K-Means聚类、模糊聚类等算法。本节提出基于信息论联合聚类的协同过滤推荐方法，以一种更加全面的方式来克服协同过滤各方面的不足，得到较满意的算法性能。联合聚类(Co-Clustering)算法是在数据矩阵的行和列2个方向上同时进行聚类，其目的是发现高度相关子空间内的簇集，即对相似的局部子模式进行聚类。对于Co-Clustering，用户和电视产品的聚类簇分别记为$C_u,C_i$，他们的联合聚类簇为$C_{u}i$，预测评$\widehat{M_{ui}}$可以根据式(5-20)计算：

$$\widehat{M_{ui}}=\overline{C_{ui}}+({\mu }_u-\overline{C_u})+(\mu -\overline{C_i})$$

(5-20)

其中，$\overline{C_{ui}}$为联合聚类簇$C_{ui}$的平均评分值，$\overline{C_u}$为用户聚类簇的平均评分值，$\overline{C_i}$为电视产品聚类簇的平均评分值，如果用户是未知的，那么令$\widehat{M_{ui}}={\mu }_i$；如果用户是未知的，那么令$\widehat{M_{ui}}={\mu }_u$；如果用户和电视产品均未知，那么$\widehat{M_{ui}}=\mu$。

Co-Clustering的基本原理是通过行聚类和列聚类2个步骤进行循环迭代直至收敛。基于信息论的联合聚类算法是将标准化后的矩阵看作一个联合概率分布，将联合聚类问题转换为信息论的最优化问题，最优的结果为最大化聚类后的随机变量间的互信息聚类。反之，最优的聚类结果就是最小化初始的随机变量与聚类后的随机变量间的互信息损失，聚类过程以最小化一个损失函数为目标。

5.6 Text-CNN

5.6.1 模型框架

卷积神经网络(Convolutional Neural Networks, CNN)主要由卷积和池化操作构成，由于卷积神经网络显著的特征提取能力，使其在图像处理及自然语言处理领域得到了广泛的应用。卷积神经网络经常用来处理具有类似网格拓扑结构的数据。例如，图像可以视为二维网格的像素点，自然语言可以视为一维的词序列。卷积神经网络可以提取多种局部特征，并对其进行组合抽象得到更高级的特征表示。实验表明，卷积神经网络能高效地对图像及文本问题进行建模处理。

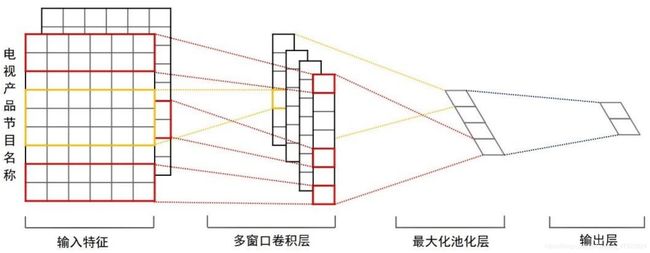
深度学习的研究中，对于类别字段常采用一位有效编码(One-Hot Encoding)方式对字段进行编码。 由于数据集中类别繁多的用户号、电视节目产品标识号的特性，使得该编码方式将无法满足神经网络输入维度的合理控制，为此，在网络的第一层使用了嵌入层，将用户号、电视节目标识号作为嵌入矩阵的索引。将每个用户号映射为维度大小为1 $\times$ 32的向量表示，输入全连接层得到用户特征。对于电视节目产品的处理，将每个产品标识号与对应产品标签（三级标签） 输入嵌入层，由于某些产品多个维度可能有多个标签，因此需要对嵌入矩阵进行求和，同样映射为维度大小为1 $\times$ 32 的向量表示。对于产品名称，则利用文本卷积神经网络进行处理， 如图5-5所示。 网络第一层为词嵌入层，由产品名称的每一个字符的嵌入向量组成的嵌入矩阵。下一层使用多个不同尺寸的卷积核在嵌入矩阵上做卷积，第三层网络为池化层，利用池化操作得到一个一维向量并使用Dropout做正则化处理，最终得到电视节目产品正题名的特征，神经网络模型如图5-6所示。

图 5-5 文本卷积神经网络实体图

图 5-6 卷积神经网络模型示意图

5.6.2 卷积层

针对文本向量进行卷积操作是提取文本向量高层次特征的一个重要过程。算法的性能与该层的卷积窗口（卷积核） 大小$h$、学习速率$\alpha$ 、卷积步长$\lambda$ 有关，本文卷积窗口的尺寸分别设置为$h=2,3,4,5$，卷积窗口个数设置为$T=20$，学习速率设置为$\alpha =0.001$，卷积步长设置为$\lambda =1$ 。 详细的文本卷积如下所示：

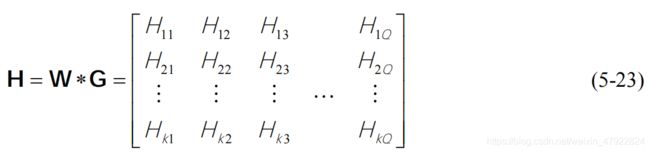
针对清洗之后的数据，我们提取了用户点播信息中的有效评分信息，该信息中共包含 527 种电视产品，由于 embedding 函数实现的功能为对嵌入矩阵的索引进行匹配，因此，需要建立 527 种电视产品标识号的匹配索引。嵌入层矩阵$W$为扩展后的电视产品节目名称矩阵，其维度为$527\times 32$， 其中$X_{ij}$代表第 $i$ 个节目名称中的第$j$ 个字符的特征向量, $X_{i:i+j}$
标识卷积窗口 $i$ 到卷积窗口 $i+j$ 进行拼接得到的特征向量，卷积核可表示为一个$h\times k$ 的矩阵，即$win\in R^{hk}$，特征图可得到 $T-h+1$个特征。矩阵$G$为卷积核函数矩阵，该矩阵大小与输入的名称数 $k$ 和卷积的窗口 $win$ 有关。

矩阵H为输入矩阵$W$与卷积核函数矩阵$G$卷积的结果。其中，$H_{ij}$代表第 $i$ 个节目名称通过$j$ 次卷积得到的向量。将矩阵$H$进行非线性处理需要非线性激活函数，常用的激活函数有 ReLu、Sigmoid 和 Tanh，这三种激活函数分别表示为如下所示，本文采用 ReLu激活函数。

$$Relu(x)=max(0,x)$$

(5-24)
$$Sigmoid(x)=\frac{1}{1+e^{-x}}$$
(5-25)
$$Tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
(5-26)

5.6.3 池化层

池化层又被称为子采样层或下采样层，在卷积层之后添加一个池化层对卷积层得到每一个特征图进行池化操作，常用的池化操作包括最大池化和平均池化，最大值池化操作选择特征图中的最大值，平均值池化选择特征图中的平均值，本文采用最大值池化操作。池化层旨在对特征图进行缩放同时降低网络的复杂度，通过最大值池化操作可以得到该卷积核的主要特征，至此每一个卷积核可以提取出一个特征。假设在卷积层第$win$个卷积核得到的特征图为$f_{win}=[f_{win1},f_{win2},...,f_{win},T-h+1]$, 池化操作可表示如式(5-27)所示，其中$down(f_{win})$表示池化操作。

$$pool-feature(win)=down(f_{win})$$

(5-27)

5.6.4 模型训练

模型的训练基于 Tensorflow 开源框架，对用户评分的拟合可规约于回归问题。经过神经网络对用户信息和产品信息的特征提取后，将两个特征作为输入信息，传入下一层全连接层，损失函数采用RMSE进行计算，采用随机梯度下降法对网络的参数进行更新，损失函数收敛曲线如图 5-7 所示，分数拟合全连接层的权重和偏置更新如图 5-8 所示。

图 5-7 损失函数收敛曲线图

图 5-8 Text-CNN 全连接层参数迭代更新示意图

5.7 推荐算法的融合

推荐系统需要面对的应用场景往往存在非常大的差异，例如热门或冷门的内容、新或老用户，时效性强或弱的结果等，对于这些不同的实际应用中，不同推荐算法往往都存在不同的适用场景，即不存在一个推荐算法，在所有情况下都胜过其他的算法。因此，本文中我们提出了一种推荐算法融合的思想，也就是充分运用不同推荐算法的各种优势，取长补短，组合形成一个强大的电视节目产品推荐系统，如图 5-9 所示。

图 5-9 推荐算法的融合示意图

为了提升推荐算法的性能，本文将上述所提出的推荐算法进行加权融合，即针对每一个用户，各算法均推荐出 TOP15 的电视节目产品，各算法推荐结果总计 90 个电视产 品。针对每种电视节目产品，各推荐算法均用于预测该用户的评分，进行线性加权取均值作为对该产品的最终评分，这样得出的用户评分更具一般性。当算法获得所有产品的最终评分后，选择 TOP15 为该用户进行推荐，各产品最终得分占评分最大值的比重作为该产品的推荐系数，从而实现模型之间的融合推荐。由于附件二中存在的大量电视节目产品并无用户的点播行为，这类电视节目产品将在冷启动问题的处理中为各用户再推 荐 TOP5 电视节目产品，每个用户总计推荐 TOP20 的电视产品。

6. 推荐系统冷启动问题

随着互联网的高速发展，人们已经步人信息过载的时代如何为用户提供个性化的服务是推荐系统的主要任务之一，然而推荐系统需要大量的用户历史行为数据作为其做出推荐的重要依据。因此对于新用户、新电视产品以及新系统来说，如何在缺少用户行为数据时对用户进行个性化推荐，即为冷启动问题。

冷启动问题主要分为以下三类：
1、用户冷启动。用户冷启动问题主要是针对如何给新用户提供个性化的推荐服务因为新用户访问系统时，系统中并没有他的历史行为数据。因此他的兴趣便无法通过分析历史行为数据进行预测，个性化的推荐也就无法进行。

2、电视产品冷启动。电视产品冷启动所要解决的主要是如何将电视产品推荐给有可能对其感兴趣的用户的问题。

3、系统冷启动。系统冷启动所要解决的主要是如何在一个没有用户、没有历史行为数据，仅有少数电视产品信息的全新的网站上对用户进行个性化推荐服务的问题。

6.1 双重聚类算法

针对以上分析，本文主要采用 K-Means 聚类来解决收视用户和电视产品冷启动问题。假设待聚类的数据集为$X=(x_i|x_i\in R^P,i=1,2,...,n)$。$K$个聚类中心分别为$M_1,M_2,...,M_k$,于是用$W_j(j=1,2,...,K)$表示聚类的 $K$ 个类别。
定义 1：两个数据对象之间的欧氏距离为：
$$d(x_i,x_j)=\sqrt{(x_i-x_j{)}^T(x_i-x_j)}$$

(5-28)
定义 2：同类别中数据对象的算术平均为：

$$M_j=\frac{1}{N}\sum _{x\in W_j}X$$

(5-29)

定义 3：聚类准则函数为：
$$E=\sum _{i=1}^k\sum _{j=1}^{n_j}d(X_j,Z_i)$$

(5-30)

在 K-Means 算法中，首先初始簇心的选择是随机的，然后通过相似度计算，再把数据集中的数据样本与最近的初始中心归为一类，不断重复这一过程，直到各个初始中心在某个精度范围内不变。

我们将用户号和电视产品根据相关的标签进行聚类，针对本题的具体聚类步骤如下：
步骤 1：首先在包含 1044 个用户的附件一中随机选择 $k$ 个用户作为聚类的初始簇心$M_i(i=1,2,...,k)$;

步骤 2：其次利用式(5-28)计算出附件一中各个用户到$M_i$的距离$d(p,M)$；

步骤 3：找到每个样本数据 $p$ 的最小的$d(p,M)$，把 $p$ 加入到与$M_i$相同的簇中；

步骤 4：完成所有样本的遍历之后，通过式(5-29)重新计算$M_i$的值，作为新的簇心；

步骤 5：重复步骤 2~步骤 4，直到目标准则函数 $E$ 取值不再变化。

K-Means 算法详细流程如下：


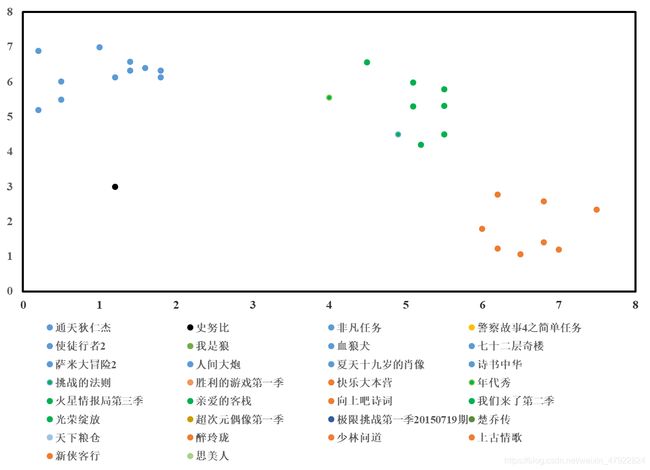
本题目中对用户的聚类是基于用户收视信息的特征，对产品进行聚类是基于产品的标签进行聚类。针对用户的聚类后的部分结果如图 6-1 所示。由图 6-1 可知，10001、10264 和 10268 等用户属于第一类，10574、10258 和 10111 等用户属于第二类，并且两个类之间的间距较大，证明聚类效果较好。针对电视产品的聚类后的部分结果如图 6-2所示。由图 6-2 中可看出，“通天狄仁杰”和“使徒行者 2”等电视节目与“年代秀”和“我们来了第二季”分属不同的电视产品类别，类间距离也同样明显。

图 6-1 针对用户的分类结果示意图

图 6-2 针对电视产品的分类结果示意图

6.2 用户冷启动问题

本文主要是基于附件一中的“用户单片点播信息”采用多种算法进行推荐，但是出现的问题就是，在附件一中的“用户收视信息”出现的用户有 1043 个，然而“用户单片点播信息”中出现的用户只有 345 个，这意味着只能通过算法对这 345 个用户进行推荐，剩下的 698 个用户无法进行推荐，所以，要设计合适的算法，对这 698 个只有收视行为信息的用户进行电视产品的推荐。根据上述的聚类结果，首先找到待推荐用户的用户类别，然后把同类别中存在点播行为用户的推荐方案推荐给该用户。

针对用户冷启动问题，一个没有任何点播行为的用户，要对其进行电视节目产品的推荐，需要根据其收视信息进行相应的推荐。首先，对附件一中的“用户收视信息”进行统计分析，找出每个用户观看的电视节目类型，然后再对这些电视节目类型为标签进行K-Means 聚类，找出相同的电视产品类别，在相同的电视产品类别中，给新用户推荐其他老用户所评价较高电视节目产品。

6.3 电视产品冷启动问题

根据附件二数据的统计分析可知，电视节目产品一共包含 2123 条记录，其中有很多电视节目产品并没有在附件一中的“用户单片点播信息”出现过，也就是说有大量的新产品并没有任何的用户收视信息，即没有用户的收视信息，因此，该类电视节目产品无法通过相应的推荐算法进行推荐，从而导致了新的电视节目产品永远是新产品，推荐算法也永远只能够推荐原有的电视节目产品，这样设计出来的推荐算法明显是不合理的，基于以上考虑，本文同时解决基于“用户”的冷启动问题和基于“产品”的冷启动问题。

针对电视产品冷启动问题，对于新的电视产品而言，它一开始并没有任何收视信息，如果按照正常的推荐方法则永远也无法被推荐到。此时需要人为的对其进行聚类，根据这些新添加的电视产品的标签进行 K-Means 聚类，在聚类之后的同类别中，把对用户推荐的 Top1 部分新的电视产品替换为部分的老产品对用户进行推荐，这样就解决了电视产品的冷启动问题。

本题目中在电视产品冷启动方面的应用是：对于融合算法推荐的 345 个用户的TOP15，需要用物品冷启动推荐剩下的 5 个电视节目产品。该五个节目产品均来源于附件二中无历史点播行为的产品。即根据用户 TOP1 产品所在的类别，随机推荐五个新产品，从而有效解决物品冷启动问题。

6.4 用户的非个性化推荐方案

针对附件三所给信息，一共包含 1329 个用户号，然而有收视信息和点播信息的用户数为 1043 个，这就导致有接近三百个用户没有任何收视信息以及点播信息。所以无论是基于协同过滤等算法的推荐系统还是基于其他算法的推荐系统，都无法对这近 300个用户进行电视产品的推荐。因此，需要对近三百个用户提供非个性化的推荐方案。

一般而言，电子商务系统的销售排行、编辑推荐、平均数值评分、个体文本评价、个体数值评分等推荐形式对所有的用户都是相同的，均可归属于非个性化推荐系统。这种推荐方式对系统及用户的要求很低，几乎不需要用户的参与。当给定的数据较为稀少的情况下，该方式不失为一种有效的策略。非个性化推荐的最简单应用便是热门排行榜，我们可以给用户推荐电视产品的热门排行榜，然后，当这部分新用户所产生的数据收集到一定的时候，再切换为个性化推荐，有针对性地推荐用户感兴趣的电视产品。

针对无任何历史行为的用户，我们采用了一种基于 K-Means 算法的非个性化推荐方案。该方案的具体策略是：首先，由上一节对所有电视产品进行聚类的基础上，把每一类的产品都对无任何数据的新用户进行一定量的推荐，保证对用户推荐的电视产品覆盖到了所有的类别中，这样可以更加全面的满足各个用户的需求。然后，根据用户的点播信息，进行以后的电视产品推荐。针对收视用户的冷启动问题大致可分为两类，一类用户是有收视行为信息但没有点播行为信息，另一类用户是收视和点播行为信息都没有。如图 6-3 所示，对这两类用户设计不同的处理方式，前者采用 K-Means 聚类对收视用户进行电视产品的推荐，后者可以采用非个性化的推荐方案对该类用户进行推荐。

图 6-3 不同类型的用户冷启动问题解决方案

7. 实验设计与分析

7.1 实验设计

对推荐算法效果的评估是整个推荐系统非常重要的一部分，通常给定一个数据集$R$，
将其分为训练数据集$R_{train}$和测试数据集$R_{test}$，而且$R_{train}\bigcup R_{test}=R$。用训练数据集来建立推荐模型，将测试数据集中的每一个用户看作目标用户，然而在推荐之前，一些项及评分保留下来，用它来度量预测评分的效果。通常假设如果推荐算法在预测保留项时效果较好，则在预测未知项时效果也好。将数据集可以分为训练数据集和测试数据集通有以下方法：(1)自动定义：随机将预设好的用户数据当作训练数据集，将其他用户数据当作测试数据集。(2)Bootstrap：随机从测试数据集中取部分数据创建训练数据集然后再用训练数据集中的其他数据集作为测试数据集。这过程的优点是对于较少的数据集来讲我们能创建较大的训练数据集并且仍有数据集可以用于测试。(3)K倍交叉混合矩阵：这里将数据集平分为K个大小相似的数据集。然后计算K次，通常使用一个数据集作为测试数据集，其他数据集用来建模。

交叉验证的理论是由Seymour Geisser所提出的是一种用来评价一个统计分析的结果是否可以推广到一个独立的数据集上的技术，即估计一个预测模型的实际应用中的准确度。它是一种统计学上将数据样本切割成较小子集的实用方法。可以先在一个子集上进行分析，而其它子集则用来做后续对此分析的确认及验证。一个交叉验证将样本数据集分成两个互补的子集，一个子集用于训练（分类器或模型）称为训练集(Training Set)；另一个子集用于验证（分类器或模型的）分析的有效性称为测试集(Testing Set)。利用测试集来测试训练得到的分类器或模型，以此作为分类器或模型的性能指标。得到高度预测精确度和低的预测误差，是研究的期望。为了减少交叉验证结果的可变性，对一个样本数据集进行多次不同的划分，得到不同的互补子集，进行多次交叉验证，采取多次验
证的平均值作为验证结果。本文采用留一法交叉验证(Leave-One-Out Cross Validation)，假设样本数据集中有N个样本数据，将每个样本单独作为测试集，其余N-1个样本作为训练集，这样得到了N个分类器或模型，用这N个分类器或模型的分类准确率的平均数作为此分类器的性能指标。留一法交叉验证可以保证每一个分类器或模型都是用几乎所有的样本来训练模型，最接近样本，这样评估所得的结果比较可靠。该方法可以确保实验没有随机因素且整个过程是可重复的。

7.2 推荐系统评测指标

典型评估预测的方法是计算预测值和真实值之间的离差，计算平均差(Mean Absolute Error, MAE)见式(7-1)所示：
$$MAE=\frac{1}{|K|}\sum _{(i,j)\in K}|M_{ij}-\widehat{M_{ij}}|$$

(7-1)

另一个常用的度量方法是标准差(Root Mean Square Deviation, RMSE)见式(7-2)所示：
$$RMSE=\sqrt{\frac{1}{|K|}\sum _{(i,j)\in K}|M_{ij}-\widehat{M_{ij}}|}$$

(7-2)

当误差较大时，RMSE效果比MAE好，因此当小的误差不是很重要时，RMSE使用较多。评价个性化推荐算法的最主要的评价指标一般选用两种指标，即准确率(Precision)和召回率(Recall)。准确率是指利用推荐算法所产生的推荐列表中用户感兴趣的资源个数占整个推荐列表的比例，表示用户对系统推荐资源感兴趣的概率。召回率是指利用推荐算法所产生的推荐列表中用户感兴趣的资源的个数与系统中用户感兴趣的全部资源的比值，表示一个用户喜欢的资源被推荐的概率。对于用户$u\in U$,令$P(u)$为给用户$u$长度为$N$的推荐列表，里面包含认为用户会打标签的电视产品。令$D(u)$表示测试集中用户$u$实际上打过标签的电视产品集合。推荐结果的准确率定义如式(7-3)所示：

$$Precision=\frac{{\sum }_{u\in U}P(U)\bigcap D(U)}{{\sum }_{u\in U}P(U)}$$

(7-3)

推荐结果的召回率定义如式(7-4)所示：
$$Recall=\frac{{\sum }_{u\in U}P(U)\bigcap D(U)}{{\sum }_{u\in U}D(U)}$$

(7-4)

准确率和召回率在一定程度上是相互制约的，为平衡两者之间的关系，引入综合衡
量指标F度量值(F-measure)，如式(7-5)所示：

$$F=\frac{2Precision\times Recall}{Precision+Recall}$$

(7-5)

7.3 结果对比与分析

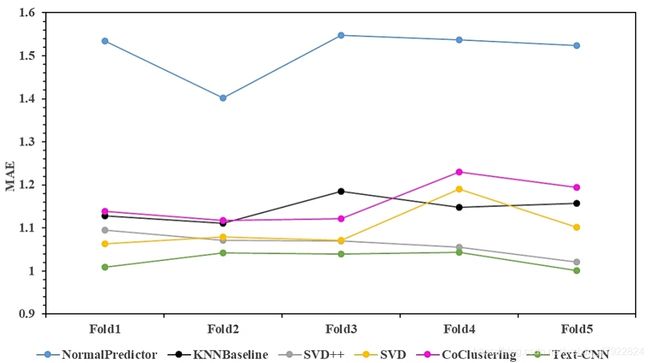
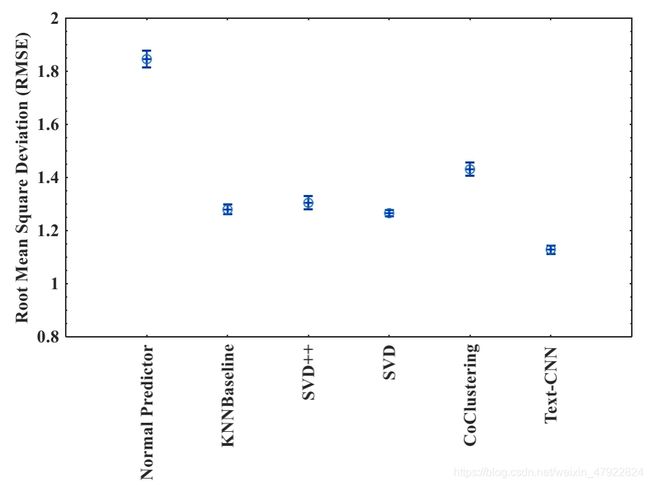
本文推荐系统的核心代码采用JetBrains PyCharm 2017.2.4 x64编写，程序运行环境为Windows 10 / Ubuntu 16.04操作系统， PC配置为32 Inter® Xeon® CPUs @ 2.6GHz/64GBRAM，其中文本卷积神经网络(Text Convolutional Neural Networks, Text-CNN)采用Google开源框架Tensorflow-gpu v1.5.0编写， Text-CNN训练运行环境为NVIDIA GeForce GTX1080/8GB VRAM。算法的测试数据集为清洗规约后的标准结构化数据集，该数据集包含用户号、电视产品标识号和用户评分三类关键指标，其中用户评分根据用户的平均观看时长以及对应电视产品播放时长的比例加权确定。本文主要测试算法运行的终止准则为Epochs=100，模型损失函数采用随机梯度下降法(Stochastic Gradient Descent, SGD)进行迭代优化， SGD学习速率设置为0.005。本节给出了六种推荐算法Normal Predictor、KNNBaseline、 SVD、 SVD++、 CoClustering和Text-CNN在RMSE和MAE两类评测指标上的测试结果，其中也给出了不同的推荐算法在准确率(Precision)、召回率(Recall)和F1指标上的性能对比，六种推荐算法的详细对比结果见图(7-1)-(7-5)所示。

图 7-1 不同推荐系统的算法测试性能对比图(RMSE:5-Folds)

图 7-2 不同推荐系统的算法测试性能对比图(MAE:5-Folds)

图 7-3 不同推荐系统的算法测试性能对比图(Precision:5-Folds)

图 7-4 不同推荐系统的算法测试性能对比图(Recall:5-Folds)

图 7-5 不同推荐系统的算法测试性能对比图(F1:5-Folds)

由图7-1和7-2中可以看出，针对RMSE和MAE两类评测指标而言，推荐算法Normal Predictor的性能最差，因为Normal Predictor首先假设所有数据服从正态分布，然后再通过样本估计参数进行预测并给出推荐方案，但是实际中的用户收视和点播数据并不服从正态分布，因此Normal Predictor算法性能表现较差。推荐算法SVD++的性能明显优于SVD的性能，而Co-Clustering和KNNBaseline算法的性能略比SVD略差，因为我们对数据规约之后加权生成的用户和电视节目产品的评分表数据非常稀疏，传统的推荐算法在稀疏评分上很难获得较好的结果。值得注意的是从图7-1和7-2中可以看出，本文所提出的基于文本卷积神经网络(Text-CNN)新型推荐算法在准确率指标上性能明显优于传统的协同过滤算法，我们通过大量测试数据的95%置信水平下的Turkey-HSD方差分析发现，我们所以出的Text-CNN推荐算法对于5-Folds交叉测试结果在RMSE和MAE上都显著占优(p<0.05)，明显优于传统的推荐算法如KNNBaseline、 SVD++和Co-Clustering， 95%置信水平如图7-6和7-7所示。因此，通过在RMSE和MAE两种评测指标上的方差分析可知，本文所提出的新型推荐算法Text-CNN对于解决电视产品营销推荐问题是有效的，该算法在5-Folds交叉测试的平均准确率(97.54%)上明显优于其他算法，平均召回率为71.06%，平均F1指数为0.8223，说明我们提出的基于文本的卷积神经网络方法Text-CNN能够精准地推荐用户需要的电视点播节目产品。此外，传统的推荐算法如SVD在F1指数上也明显占优，说明该算法也是一种解决电视产品营销推荐问题的有效推荐算法。

图 7-6 不同推荐系统的算法的 ANOVA Turkey-HSD 95%置信区间图(RMSE:5-Folds)

图 7-7 不同推荐系统的算法的 ANOVA Turkey-HSD 95%置信区间图(MAE:5-Folds)

7.3.1 问题一结果分析

问题一所需提交的结果为每个用户的营销推荐方案，并且要给出不同电视产品的推荐指数。根据营销推荐方案，可以分析出用户的收视偏好信息，且进一步通过用户的收视信息可以分析出用户的家庭主要成员。

图 7-8 算法推荐给用户的电视节目类型表

分析收视偏好的主要方法就是寻找算法为用户推荐的Top20的电视产品中各个类型的电视节目所占的比例。如果相同类型的电视节目所占的比例越高，就证明此类型的电视节目备受用户青睐，相应地如果某种类型的电视节目被算法推荐的较少甚至都没有推荐，就说明用户对此类节目的喜欢程度一般，通过采用这种方法，我们可以分析出每个用户的收视偏好。具体举例来说，对于10853号用户，我们所设计的推荐算法给他推荐的20部电视产品种类如图7-8所示，其中包含9部动画、 1部综艺、 7部电视剧、 3部科教，在这20部电视产品中动画和电视剧的类别数量明显比其他更高，由此来看，该用户更喜欢看动画和电视剧，问题一推荐结果如图7-9所示。

图 7-9 算法推荐给用户的电视节目名称表
基于以上所分析的用户收视偏好，我们分别对全部用户进行用户画像。因为家庭成员中小孩、成年人和老人的收视偏好都是不同的，甚至是同样是成年人，他们的收视偏好也有很大差别。例如有的人喜欢看战争片，而有的人却喜欢看喜剧片，所以根据用户的收视偏好，我们可以分析出用户家庭大致所包含的成员并对用户画像。例如，图7-6中所示的10853号用户，从收视偏好来看，此用户更喜欢动画和电视剧，说明这个家庭成员中有少儿或成年人，同时由于我们所设计的推荐算法对其推荐了三部科教片，因此表明这个家庭的成年人的受教育程度较高。

7.3.2 问题二结果分析

对于问题二而言， 一共需要提交“用户标签体系表”、 “产品标签体系表”、 “用户收视数据标签”、 “产品数据标签”、 “用户数据标签”和“问题二推荐结果表”共六个表。 根据“用户标签体系表”、 “用户收视数据标签”、 “用户数据标签”和“推荐结果表”这四个表， 可以得到每个用户的相应特征。 也就是说，可以通过用户的各种点播信息以及收视信息来挖掘用户的收视行为特征，并根据这些特征对用户进行收视行为分析。有了这些用户的收视行为，就可以为用户画像并能够对用户进行电视产品的精准化推荐。例如，我们对某个用户的标签是“上午”、 “中午”、 “晚上”、 “动画”、 “老人”和“体育”等， 就可以对该用户画像，可以判断出用户的家庭成员复杂，人员多并且收视偏好多样，这样算法推荐的时候就可以推荐一些包含范围比较广的电视节目产品套餐。

从“产品标签体系表”和“产品数据标签”这两个表中， 可以获取电视节目产品的标签，这些标签代表了这些电视产品所对应的类型，通过把这些电视产品类型进行分类，可以把不同的电视产品类别推荐给收视偏好不同的用户。 例如表7-1中， “加菲猫和他的朋友们第三季仙人掌的传说”、 “加菲猫和他的朋友们第三季法律之鹰”、 “家庭教师”和“画江湖之灵主”这四部电视节目的标签为“少儿”， 因此， 可以把这四部电视节目一并推荐给家庭成员中有少儿的用户。 又比如“谁寄锦书来”、 “一粒红尘”和“流星花园”这三部电视节目的标签中有“情感剧”， 可以把这三部电视节目推荐给用户家庭成员有“青年”或者“女性”标签的用户。 问题二的推荐结果如图7-10所示。

表 7-1 电视节目产品标签表

图 7-10 算法推荐给用户的电视节目类型表

参考文献

[1] GOLDBERG D, NICOLSD. Using collaborative filtering to weave an information tapestry[J].Communications of the ACM,1992,35(12):61-70.

[2] Prota, T., Bispo, A., & Ferraz, C. (2015). A literature review of recommender systems in the television domain. Expert Systems with Applications An International Journal, 42(22), 9046-9076.

[3] Lü, L., Medo, M., Chi, H. Y., Zhang, Y. C., Zhang, Z. K., & Zhou, T. (2012). Recommender systems. Physics Reports, 519(1), 1-49.

[4] DietmarJannach. 推荐系统[M]. 人民邮电出版社, 2013.

[5] 周轶伦. 基于协同过滤的网络电视推荐系统的研究与实现[D]. 中山大学, 2009.