LeetCode——回溯篇（三）

刷题顺序及思路来源于代码随想录，网站地址：https://programmercarl.com

目录

46. 全排列

47. 全排列 II

332. 重新安排行程

51. N 皇后

37. 解数独

---

 

46. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;

/**
 * @author light
 * @Description 全排列
 * @create 2023-08-30 9:36
 */
public class PermuteTest {
	public static void main(String[] args) {
		Scanner input=new Scanner(System.in);
		int n=input.nextInt();
		int[] nums=new int[n];
		for (int i = 0; i < n; i++) {
			nums[i]=input.nextInt();
		}
		System.out.println(permute(nums));
	}
	public static List> res=new ArrayList<>();
	public static List path=new ArrayList<>();
	public static List> permute(int[] nums) {
		int[] used=new int[nums.length]; //记录数组中哪个元素已经使用过了
		Arrays.fill(used,0);
		backtracking(nums,used);
		return res;
	}

	private static void backtracking(int[] nums,int[] used) {
		if(path.size()==nums.length){
			res.add(new ArrayList<>(path));
			return;
		}
		for (int i = 0; i < nums.length; i++) {
			if(used[i]==0){
				path.add(nums[i]);
				used[i]=1;
				backtracking(nums,used);
				//回溯
				path.remove(path.size()-1);
				used[i]=0;
			}
		}
	}
}

47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;

/**
 * @author light
 * @Description 全排列II
 *
 *给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。
 *
 * (需要去重
 * @create 2023-08-30 9:59
 */
public class PermuteUniqueTest {
	public static void main(String[] args) {
		Scanner input=new Scanner(System.in);
		int n=input.nextInt();
		int[] nums=new int[n];
		for (int i = 0; i < n; i++) {
			nums[i]=input.nextInt();
		}
		System.out.println(permuteUnique(nums));
	}

	public static List> res=new ArrayList<>();
	public static List path=new ArrayList<>();

	public static List> permuteUnique(int[] nums) {
		Arrays.sort(nums);
		int[] used=new int[nums.length]; //记录数组中哪个元素已经使用过了--同时去重
		Arrays.fill(used,0);
		backtracking(nums,used);
		return  res;
	}

	private static void backtracking(int[] nums, int[] used) {
		if(path.size()== nums.length){
			res.add(new ArrayList<>(path));
			return;
		}
		for (int i = 0; i < nums.length; i++) {
			//去重逻辑
			if(i>0&&nums[i]==nums[i-1]&&used[i-1]==0){
				continue;
			}
			if(used[i]==0){ //数组元素还未使用
				path.add(nums[i]);
				used[i]=1;
				backtracking(nums,used);
				//回溯
				path.remove(path.size()-1);
				used[i]=0;
			}
		}
	}
}

332. 重新安排行程

给你一份航线列表 tickets ，其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。

所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。

• 例如，行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小，排序更靠前。

假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。

 

public class FindItineraryTest {

	public LinkedList res;
	public LinkedList path=new LinkedList<>();

	public List findItinerary(List> tickets) {
		//对集合中元素降落地点排序
		Collections.sort(tickets, new Comparator>() {
			@Override
			public int compare(List o1, List o2) {
				return o1.get(1).compareTo(o2.get(1));
			}
		});
		path.add("JFK"); //从JFK出发
		boolean[] used=new boolean[tickets.size()]; //判断元素是否重复
		Arrays.fill(used,false);
		backtracking((ArrayList)tickets,used);
		return res;
	}

	private boolean backtracking(ArrayList> tickets, boolean[] used) {
		//终止条件
		if(path.size()==tickets.size()+1){
			res=new LinkedList<>(path);  //只有一条路径
			return true;
		}

		for (int i = 0; i < tickets.size(); i++) {
			//未使用重复元素并且path中最后一个元素的值等于tickets数组航班中的起飞航班，则将降落航班加入path中
			if(!used[i]&&tickets.get(i).get(0).equals(path.getLast())){
				path.add(tickets.get(i).get(1));
				used[i]=true;
				if(backtracking(tickets,used)){
					return true;
				}
				//回溯
				used[i]=false;
				path.removeLast();
			}

		}
		return false;
	}

}

51. N 皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

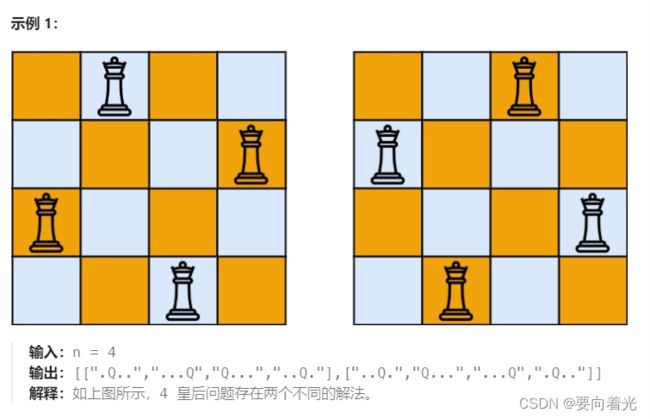
给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

 

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;

/**
 * @author light
 * @Description N皇后
 * @create 2023-08-30 11:13
 */
public class SolveNQueensTest {
	public static void main(String[] args) {
		Scanner input=new Scanner(System.in);
		int n=input.nextInt();
		System.out.println(solveNQueens(n));
	}


	public static List> res=new ArrayList<>();

	public static List> solveNQueens(int n) {
		char[][] chessboard = new char[n][n];
		for (char[] c : chessboard) {
			Arrays.fill(c, '.');
		}
		backtracking(chessboard,n,0);
		return res;
	}

	//row:行--控制递归深度
	private static void backtracking(char[][] chessboard, int n, int row) {
		//终止条件--收获结果
		if(row==n){
			res.add(arrayToList(chessboard));
			return;
		}
		//单层递归逻辑
		for (int col = 0; col < n; col++) {
			//判断是否合法位置
			if(isValid(chessboard,row,col,n)){
				chessboard[row][col]='Q';
				backtracking(chessboard,n,row+1);
				//回溯
				chessboard[row][col]='.';
			}
		}
	}

	private static List arrayToList(char[][] chessboard) {
		List path=new ArrayList<>();
		for (int i = 0; i < chessboard.length; i++) {
			path.add(String.valueOf(chessboard[i]));
		}
		return path;
	}

	/*
	验证棋盘是否合法
		按照如下标准去重：
			1.不能同行
			2.不能同列
			3.不能同斜线 （45度和135度角）
	 */
	private static boolean isValid(char[][] chessboard, int row, int col, int n) {
		检查行  （可以不用检查行，每一次递归，row+1
		//for (int i = 0; i < col; i++) {
		//	if(chessboard[row][i]=='Q'){
		//		return false;
		//	}
		//}

		//检查列
		for (int i = 0; i < row; i++) {
			if(chessboard[i][col]=='Q'){
				return  false;
			}
		}

		//检查斜线--45度
		for (int i = row-1,j=col-1; i>=0&&j>=0 ; i--,j--) {
			if(chessboard[i][j]=='Q'){
				return  false;
			}
		}

		//检查斜线--135度
		for (int i = row-1,j=col+1; i >=0&&j

37. 解数独

编写一个程序，通过填充空格来解决数独问题。

数独的解法需 遵循如下规则：

1. 数字 1-9 在每一行只能出现一次。
2. 数字 1-9 在每一列只能出现一次。
3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

数独部分空格内已填入了数字，空白格用 '.' 表示。

/**
 * @author light
 * @Description 解数独
 *
 * @create 2023-08-30 12:19
 */
public class SolveSudokuTest {
	public static void solveSudoku(char[][] board) {
		backtracking(board);
	}

	private static boolean backtracking(char[][] board) {

		for (int i = 0; i < 9; i++) { //行
			for (int j = 0; j < 9; j++) { //列
				if(board[i][j]!='.'){
					continue;
				}else {

					for (char k = '1'; k <='9' ; k++) {
						if(isValid(i,j,k,board)){
							board[i][j]=k;
							if(backtracking(board)){
								return true;
							}
							//回溯
							board[i][j]='.';
						}
					}
					// 9个数都试完了，都不行，那么就返回false
					return false;
				}
			}
		}
		return true;
	}

	/**
	 * 判断棋盘是否合法有如下三个维度:
	 *     同行是否重复
	 *     同列是否重复
	 *     9宫格里是否重复
	 */
	private static boolean isValid(int row, int col, char val,char[][] board) {
		//同行是否重复
		for (int i = 0; i < 9; i++) {
			if(board[row][i]==val){
				return false;
			}
		}

		//同列是否重复
		for (int i = 0; i <9; i++) {
			if(board[i][col]==val){
				return false;
			}
		}

		//9宫格里是否重复
		int startRow=(row/3)*3;
		int startCol=(col/3)*3;
		for (int i = startRow; i