SPSS--s04典型相关分析

典型相关基本原理

 典型相关分析是主成分分析和因子分析的进一步发展 ,是研究两组变量间的相互依赖关系 ,把两组变量之间的相互关系变为研究两个新的变量之间的相关,而且又不抛弃原来变量的信息 ,这两个新的变量分别由第一组变量和第二组变量的线性组合构成 ,并且两组变量的个数可以是不同的 ,两组变量所代表的内容也可以是不同的。

例如：某种药物的不同剂型、剂量、给药途径、给药时间等为一类因素，而给药后对人体各系统（神经系统、循环系统、呼吸系统、消化系统等）产生的反应为另一因素，对于这种情况就需要从两组整体上来分析“处理”与“效应”之间的相关性。

典型性相关分析与简单相关分析相比 ,简单相关分析有时可能受某些因素的影响 ,反映的是表面的而非本质的联系 ,甚至有时是假象。所以 ,典型性相关分析在相关分析中有其独特的作用。

典型相关分析的线性组合

设两组变量X1、X2、……、Xp 与Y1、Y2、……、Yp ， 则其线性组合可表示为：

这种线性组合被称为第一典型相关变量，也可以推广到一般情况，即第 i （i ≧ 1）典型相关变量。

典型相关分析需满足的条件

典型相关分析是在原始数据满足一定条件和假设的前提下进行的 , 这些条件包括原始变量要服从多元正态分布, 样本容量至少要大于原始变量个数（一般为变量个数的10 ~20 倍）,这些假设包括两组变量之间要具有相关性,每组原始变量中能够综合出典型变量, 即原始变量组内要有一定的相关性等 。若这些条件和假设无法满足 ,就不能进行典型相关分析。

典型相关分析一般步骤

案例分析

探讨小学生的生长发育指标与身体素质的相关关系，某市对小学生的体质进行了调查。 对 84 例 10岁男孩的四项生长发育指标：肺活量（L）、身高（cm）、体重（Kg）、胸围（cm）与四项反映身体素质的指标：50m 跑（s）、跳高（cm）、跳远（m）、实心球掷远（m）进行典型相关分析。（数据来源：医学统计学第4版，孙振球等主编）

数据视图

变量视图

手把手教你

在统计软件SPSS23.0及以下版本无相应的菜单操作，故需要使用语法来完成。

【一】新建语法：单击“文件”“新建”“语法”

【二】弹出如下所示界面，输入语法代码：

INCLUDE'C:\ProgramFiles\IBM\SPSS\Statistics\22\Samples\English\Canonical correlation.sps'.    这段语句为''Canonical correlation.sps"的安装位置，需要输入自己文件的位置

CANCORR SET1 = x1 x2 x3  x4  / SET2 = y1 y2 y3 y4 . 

【三】输入语法完毕后，点击“运行”即可

结果解析

①

变量x1 x2 x3 x4 之间的相关系数；变量y1 y2 y3 y4 之间的相关系数；

②

两组变量之间的相关系数

③

第一列为 各个典型相关系数，依次为λ1=0.871， λ2=0.312， λ3=0.164， λ4=0.053 ；第二列是对各典型相关系数的检验，由结果可知，第一典型相关系数在α=0.05 的情况下有统计学意义；

④

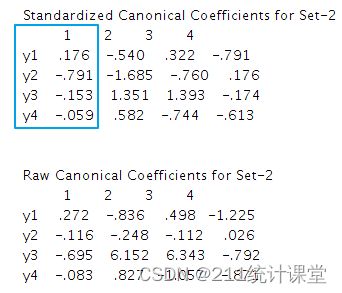
标准化的U典型相关变量与未标准化（原始）的U典型相关变量

标准化的V典型相关变量与未标准化（原始)的V典型相关变量

标准化的第一典型相关变量可表示为：

U1=-0.099X1-0.462X2-0.066X3-0.525X4

V1=0.176Y1-0.791Y2-0.153Y3-0.059Y4

同理可写出其它的典型相关变量

通过以上表达式，可以看出U1 主要受X2（身高）和X4（胸围）的影响较大；V1主要受Y2（跳高）和Y1（50m跑）的影响较大；除此之外，通过典型相关系数的正负可以判断变量X与变量Y的正负相关，以变量Y1为例，U1中的各变量与Y1呈负相关。