Leetcode 易错题整理（二）40. 45. 46. 47. 49. 56. 62. 63.

40. 组合总和 II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

**注意：**解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

组合总和1：没有重复数组元素，为了保证结果不重复，我们只要保证下次递归时访问的数大于等于上次递归时的数即可。

组合总和2：有重复元素，每个元素只用一遍即可。

最开始我想的就是每次用完一个数组元素，下次递归把这个数组元素移除掉，用一个少一位的数组继续递归即可。后来发现没有那么简单。

for(int i=pre;i<candidates.length;i++){
                if(target>=candidates[i]){
                    List<Integer> newList=new ArrayList<>(tempList);
                    newList.add(candidates[i]);
                    int[] temp=new int[len-1];
                    int cnt=0;
                    for(int j=0;j<len;j++){
                        if(j!=i)temp[cnt++]=candidates[j];
                    }
                    subFunc(resList,newList,temp,target-candidates[i],len-1,i);
                }
            }

这样的代码会出现一个问题：循环检测到第一个数字1，然后使用去掉1的数组进行递归；然后循环下一轮碰到的还是数字1，也是用去掉一个1的数组进行递归，实际上是两个重复的结果。可见这位大佬的图片参考：

其实很简单解决，我们只需要加一句话：当此轮循环数和上一轮循环数相同的时候跳过本轮循环即可。

完整代码：

class Solution {
    public void subFunc(List<List<Integer>> resList,List<Integer> tempList, int[] candidates,int target, int len, int pre){
        if(target<0)return;
        if(target==0){resList.add(tempList);return;}
        else {
            for(int i=pre;i<candidates.length;i++){
                if(target>=candidates[i]){
                    if(i>0&&candidates[i]==candidates[i-1])continue;
                    List<Integer> newList=new ArrayList<>(tempList);
                    newList.add(candidates[i]);
                    int[] temp=new int[len-1];
                    int cnt=0;
                    for(int j=0;j<len;j++){
                        if(j!=i)temp[cnt++]=candidates[j];
                    }
                    subFunc(resList,newList,temp,target-candidates[i],len-1,i);
                }
            }
        }
        
    }
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        List<List<Integer>> resList=new ArrayList<>();
        Arrays.sort(candidates);
        subFunc(resList,new ArrayList<>(),candidates,target,candidates.length,0);
        return resList;
    }
}

45. 跳跃游戏 II

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

• 0 <= j <= nums[i]
• i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

使用贪心算法。

思路
如果某一个作为 起跳点 的格子可以跳跃的距离是 3，那么表示后面 3 个格子都可以作为 起跳点。 11. 可以对每一个能作为 起跳点 的格子都尝试跳一次，把 能跳到最远的距离 不断更新。

如果从这个 起跳点 起跳叫做第 1 次 跳跃，那么从后面 3 个格子起跳 都 可以叫做第 2 次 跳跃。

所以，当一次 跳跃 结束时，从下一个格子开始，到现在 能跳到最远的距离，都 是下一次 跳跃 的 起跳点。 31. 对每一次 跳跃 用 for 循环来模拟。

跳完一次之后，更新下一次 起跳点 的范围。
在新的范围内跳，更新 能跳到最远的距离。
记录 跳跃 次数，如果跳到了终点，就得到了结果。

图解

作者：Ikaruga
链接：https://leetcode.cn/problems/jump-game-ii/solutions/36035/45-by-ikaruga/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

class Solution {
    public int jump(int[] nums) {
        int end=0;
        int step=0;
        int maxLocation=0;
        for(int i=0;i<nums.length-1;i++){
            maxLocation=Math.max(maxLocation,i+nums[i]);
            if(i==end){
                step++;
                end=maxLocation;
            }
        }
        return step;
    }
}

每次我们在 i 到 end 范围内找一下看最远能跳到哪里，最远能跳到的地方作为下一个区间的 end。

46. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

全排列算法：回溯。

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        int len=nums.length;
        List<List<Integer>> resList=new ArrayList<>();
        List<Integer> outList=new ArrayList<>();
        for(int num:nums){
            outList.add(num);
        }
        backtrack(resList,outList,0,nums.length);
        return resList;
    }

    public void backtrack(List<List<Integer>> resList, List<Integer> outList, int first, int len){
        if(first==len){
            resList.add(new ArrayList<Integer>(outList));
        }
        for(int i=first; i<len;i++){
            Collections.swap(outList, first, i);
            backtrack(resList, outList, first+1, len);
            Collections.swap(outList, first, i);
        }
    }
}

47. 全排列 II

出现了重复的元素。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]

也比较简单。从结论上来说，for 循环做交换的时候，这个位置的重复数字只能交换过来一次，后面就不要交换这个数字过来了。

Set<Integer> set=new HashSet<>();
        for(int i=first; i<len;i++){
            if(!set.contains(outList.get(i))){
                set.add(outList.get(i));
                Collections.swap(outList, first, i);
                backTrack(resList,outList,first+1,len);
                Collections.swap(outList, first, i);
            }
        }

49. 字母异位词分组

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

字母异位词 是由重新排列源单词的所有字母得到的一个新单词。

示例 1:

输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

这种就是利用哈希表来唯一存储映射关系。重点在于如何划分唯一键值。

一种方法是：把字符串排序后可以作为唯一键值。比如 aet, ant。

另一种方法是，不同字符串组合各个字母出现的个数也不同，可以把“字母”+”出现次数“+”字母“……组合成一个字符串作为键值。这个优点在于不用排序每一个字符串，我们可以弄一个长度26的空数组，每次遍历一个字符串把其中的字母出现情况统计到数组中，最后从 a-z 遍历数组统计。这里我只尝试了方法一。

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        Map<String, List<String>> hashMap=new HashMap<>();
        for(String str:strs){
            char[] array=str.toCharArray();
            Arrays.sort(array);
            String key=new String(array);
            if(hashMap.containsKey(key)){
                hashMap.get(key).add(str);
            }
            else {
                List<String> list=new ArrayList<>();
                list.add(str);
                hashMap.put(key,list);
            }
        }
        return new ArrayList<List<String>>(hashMap.values());
    }
}

56. 合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

思路：首先数组按第一个元素排序，然后每个数组和后面数组比较，如果他的第二个元素大于后面数组的第一个元素，则这两个数组可以合并，选取这两个数组第二个元素更大的作为新的第二个元素（结束地址）。

对我来说最重要的是 List to Array 的写法。

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals, new Comparator<int[]>(){
            public int compare(int[] interval1, int[] interval2){
                return interval1[0]-interval2[0];
            }
        });
        int ptr=0;
        int[] curArray=new int[2];
        int len=intervals.length;
        List<int[]> resList=new ArrayList<>();
        while(ptr<len){
            curArray[0]=intervals[ptr][0];
            curArray[1]=intervals[ptr][1];
            while(ptr<len-1&&curArray[1]>=intervals[ptr+1][0]){
                curArray[1]=curArray[1]>intervals[ptr+1][1]?curArray[1]:intervals[ptr+1][1];
                ptr++;
            }
            int[] temp=new int[2];
            temp[0]=curArray[0];
            temp[1]=curArray[1];
            resList.add(temp);
            ptr++;
        }
        return resList.toArray(new int[resList.size()][]);
    }
}

62. 不同路径

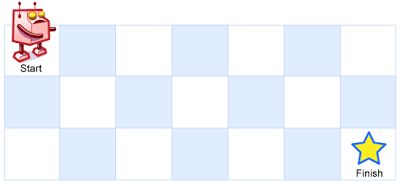
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28

思路：公式计算：(m+n-2)!/(m-1)!/(n-1)!，即为：横竖一共走 m+n-2 步，无视 m-1 n-1 步内部顺序，找出所有可能组合。

不过直接套公式 long 也会超长度。我们可以在一个公式里完成乘除运算。

class Solution {
    public int uniquePaths(int m, int n) {
        
        long res=1;
        for(int i=m,j=1;j<n;i++,j++){
            res=res*i/j;
        }
        return (int)res;
    }
}

63. 不同路径 II

在上一题基础上，路径中会添加几个障碍物。数组元素=0是可走的路，数组元素=1是障碍物。

我一开始以为障碍物只有一个，因此只写了没有障碍物的情况-（出发点走到有障碍物的情况*障碍物走到终点的情况）。

多个障碍物解法：动态规划，其实到每个位置 [i,j] 的可能性都是到 [i,j-1] 的可能性+到 [i-1,j] 的可能性。到障碍物点可能性=0.

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int arrLen=obstacleGrid.length;
        int eleLen=obstacleGrid[0].length;
        int[] f=new int[eleLen];
        f[0]=obstacleGrid[0][0]==1?0:1;
        for(int i=0;i<arrLen;i++){
            for(int j=0;j<eleLen;j++){
                if(obstacleGrid[i][j]==1){f[j]=0;
                continue;}
                if(j-1>=0)f[j]+=f[j-1];
            }
            
        }
        return f[eleLen-1];
    }
}