NMS（非极大值抑制）的 Python 实现

非极大值抑制（Non-Maximum Suppression，NMS）是一种在目标检测中常用的技术。

NMS的目的是消除重叠区域中冗余的边界框，并选择最具代表性的目标作为最终结果。通过调整重叠阈值，可以控制NMS的严格程度，从而影响输出的目标数量和召回率。

1. NMS的步骤

实现NMS的步骤如下：

输入：一组候选边界框（通常是由目标检测器生成的），每个边界框都有一个得分值表示其置信度。
按照得分值降序排列所有候选边界框。
选择得分最高的边界框，将其添加到最终的结果列表中，并从候选边界框列表中移除。
计算当前选择的边界框与其他候选边界框的重叠区域（例如，交并比IoU）。
从剩余的候选边界框中移除重叠区域高于一定阈值的边界框。
重复步骤3至步骤5，直到所有候选边界框都被处理完毕。
返回最终的结果边界框列表，这些边界框代表了在重叠区域中最具代表性的目标。

2. Python代码

参考博客：NMS的python实现

code：

import numpy as np
import matplotlib.pyplot as plt


# 自定义数据
# 存储方式: 左下角(x1,y1)坐标，右上角(x2,y2)坐标，置信度 score
Boxes = np.array([[100, 100, 210, 210, 0.72],
                  [250, 250, 400, 400, 0.8],
                  [220, 220, 320, 370, 0.92],
                  [100, 150, 235, 200, 0.79],
                  [230, 240, 355, 350, 0.81],
                  [220, 230, 315, 340, 0.9],
                  [140, 175, 255, 270, 0.95]])


def nms(boxes, iou_thresh):
    # 每个 box 的坐标和置信度
    x1 = boxes[:, 0]
    y1 = boxes[:, 1]
    x2 = boxes[:, 2]
    y2 = boxes[:, 3]
    scores = boxes[:, 4]

    # 每个 box 的面积，areas = [12321. 22801. 15251.  6936. 13986. 10656. 11136.]
    # 需要 +1 的原因：若某个 box 的 x 坐标的像素范围为 [5,10]，则共占据 6 个像素，因此 6 = 10-5+1
    areas = (y2 - y1 + 1) * (x2 - x1 + 1)

    # keep_boxes 用于存放执行 NMS 后剩余的 boxes
    keep_boxes = []

    # 取出置信度从大到小排列的索引，其中 scores.argsort() 返回的是数组值从小到大的索引
    # scores = [0.72  0.8  0.92  0.79  0.81  0.9  0.95]
    # index = [  6     2     5    4     1     3    0]
    index = scores.argsort()[::-1]

    while len(index) > 0:
        # 取出置信度最大的 box,将其放入 keep 中，并判断其他 box 是否可以与之合并
        i = index[0]
        keep_boxes.append(i)

        # np.maximum(arr:list, x:int)表示计算arr中每一个元素与常数 x 之间的最大值
        # 如 i=6时，x1[i]=140，x1[index[1:]] = [220. 220. 230. 250. 100. 100.]
        # 则 x11 = [220. 220. 230. 250. 140. 140.]
        x1_overlap = np.maximum(x1[i], x1[index[1:]])
        y1_overlap = np.maximum(y1[i], y1[index[1:]])
        x2_overlap = np.minimum(x2[i], x2[index[1:]])
        y2_overlap = np.minimum(y2[i], y2[index[1:]])

        # 计算重叠部分的面积，若没有不重叠部分则面积为 0
        w = np.maximum(0, x2_overlap - x1_overlap + 1)
        h = np.maximum(0, y2_overlap - y1_overlap + 1)
        overlap_area = w * h

        # 计算 iou（交并比）
        # 第一次 while 循环中，ious = [0.072  0.070  0.031  0.003  0.155  0.119]
        ious = overlap_area / (areas[i] + areas[index[1:]] - overlap_area)

        # 合并重叠度最大的 box，即只保留 iou < iou_thresh 的 box
        # 第一次 while 循环中，np.where(ious <= iou_thresh) = (array([0, 1, 2, 3, 5], dtype=int64),)
        # 因为 np.where(ious <= iou_thresh) 的数据结构是 tuple 里面包含了一个 list，所以要用 [0] 取出 list
        idx = np.where(ious <= iou_thresh)[0]

        # idx + 1 = [1 2 3 4 6]
        # index = index[idx + 1] = [2 5 4 1 0]
        # 这里为什么要将 idx + 1 呢？因为 index 是 ious 的索引，而 ious 是去除掉 index 的第一个元素对应的 box 得到的，
        # 所以 ious 的索引 +1 对应的 box 才是 index 相同索引对应的 index
        # 因为 len(ious)<=len(index)，所以 len(index[idx + 1])<=len(index)，所以 while 循环中 index 的元素数量越来越少
        index = index[idx + 1]

    return keep_boxes


def plot_bbox(dets, c='k'):
    x1 = dets[:, 0]
    y1 = dets[:, 1]
    x2 = dets[:, 2]
    y2 = dets[:, 3]
    plt.plot([x1, x2], [y1, y1], c)
    plt.plot([x1, x1], [y1, y2], c)
    plt.plot([x1, x2], [y2, y2], c)
    plt.plot([x2, x2], [y1, y2], c)
    plt.title("NMS")


if __name__ == '__main__':
    plt.figure(1)
    ax1 = plt.subplot(1, 2, 1)
    ax2 = plt.subplot(1, 2, 2)

    # before nms
    plt.sca(ax1)
    plot_bbox(Boxes, 'g')

    # after nms
    keep_boxes = nms(Boxes, iou_thresh=0.15)
    plt.sca(ax2)
    plot_bbox(Boxes[keep_boxes], 'r')

    # 设置两个子图的坐标范围，防止坐标范围不一致
    ax1.set_xlim([50, 450])
    ax1.set_ylim([50, 450])
    ax2.set_xlim([50, 450])
    ax2.set_ylim([50, 450])
    plt.show()

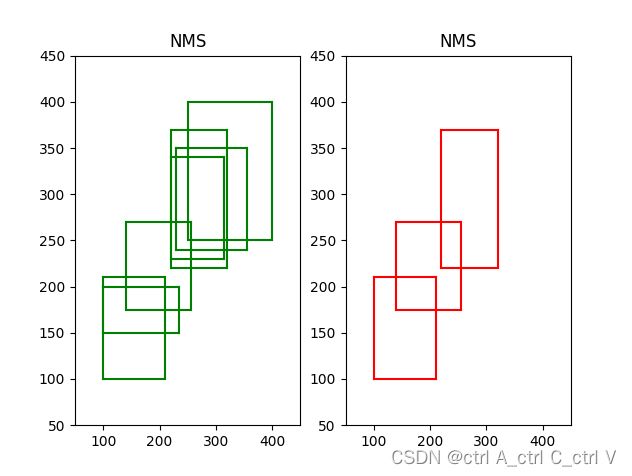
效果演示: