搜索算法总结

搜索算法

被可爱的女孩子问懵了，学艺不精，翻车的我决定重新理解一下这几个算法

wiki真是个好东西，它真的我哭死

1. 深度优先搜索（Depth-First-Search, DFS）

不多说，遍历顺序如下图序号

2. 广度优先搜索（Breadth-first search, BFS）

也不多说，遍历顺序在图中

3. 启发式搜索策略

3.1 爬山法（Hill climbing）

爬山法是完完全全的贪心法，每次都鼠目寸光的选择一个当前最优解，因此只能搜索到局部的最优值。

例题： 以八数码为例


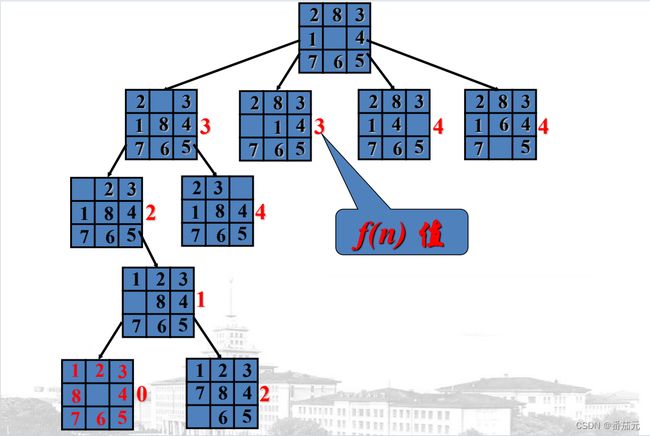
每一步都选择局部最优，最后很可能陷入一个局部最优解。

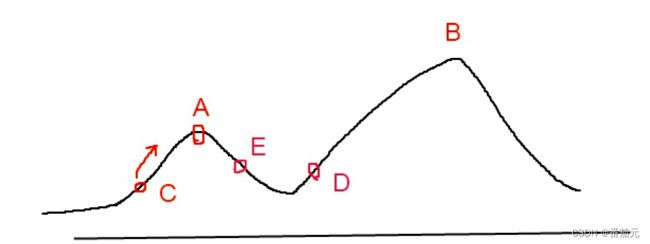
那么能不能优化一下呢？当它找到某个山顶时，可以给个随机数，随机一下，就有概率找到更优的解（同时也承担着找到更差解的风险）。下面以模拟退火为例，

模拟退火其实也是一种贪心算法，但是它的搜索过程引入了随机因素.。模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以上图为例，模拟退火算法在搜索到局部最优解A后，会以一定的概率接受到E的移动。也许经过几次这样的不是局部最优的移动后会到达D点，于是就跳出了局部最大值A。

3.2 最佳优先搜索（Best-first search）

首先看一下wikipedia对 Best-first search 算法的解释

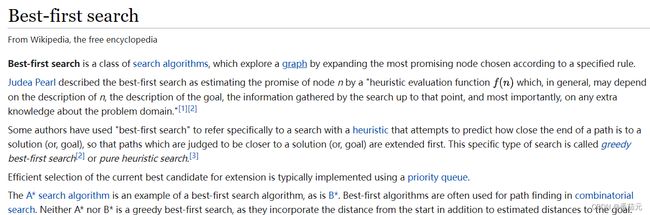
说法不是很统一，大概是两种

1. 可以是 A* 这样的启发式函数，既用到了从起点到当前点的评价，也用到了从当前点到目标点的估价。

2. 可以是 greedy best-first search 基于贪心策略的优先搜索，即只用到从当前点到达目标点的估价。

这里我选择第二种来理解，wiki 给出的伪代码如下，看算法名字就很形象，贪心的 BFS

Greedy BFS

Using a greedy algorithm, expand the first successor of the parent. After a successor is generated:

使用贪心算法，将队列中的所有结点排序后，将队列中位于队首的结点出队，将其所有子节点拓展进队列

1. If the successor’s heuristic is better than its parent, the successor is set at the front of the queue (with the parent reinserted directly behind it), and the loop restarts.

   如果后代节点的估价更优，则可以放在父节点的前面。（实现过程可以是用普通队列让所有节点出队，重新排序后入队；也可以使用优先队列（堆），这样每次优先队列的队首（堆顶）都是当前队列中估价最优的节点）

2. Else, the successor is inserted into the queue (in a location determined by its heuristic value). The procedure will evaluate the remaining successors (if any) of the parent.

   如果新加入的节点估价不好，按照估价排序放在队列中的对应位置就行

Below is a pseudocode example of this algorithm, where queue represents a priority queue which orders nodes based on their heuristic distances from the goal. This implementation keeps track of visited nodes, and can therefore be used for undirected graphs. It can be modified to retrieve the path.

下面是该算法的伪代码示例，其中 queue 表示优先级队列，它根据节点与目标的启发式距离对节点进行排序。

procedure GBS(start, target) is:
  mark start as visited
  add start to queue
  while queue is not empty do:
    current_node ← vertex of queue with min distance to target
    remove current_node from queue
    foreach neighbor n of current_node do:
      if n not in visited then:
        if n is target:
          return n
        else:
          mark n as visited
          add n to queue
  return failure 

可以看到，每个节点都会被 visited 标记，即每个节点只能访问一次，每次都是贪心的选择下一步的最优解，不回头更新之前的搜索过的结果，可能会陷入局部最优。

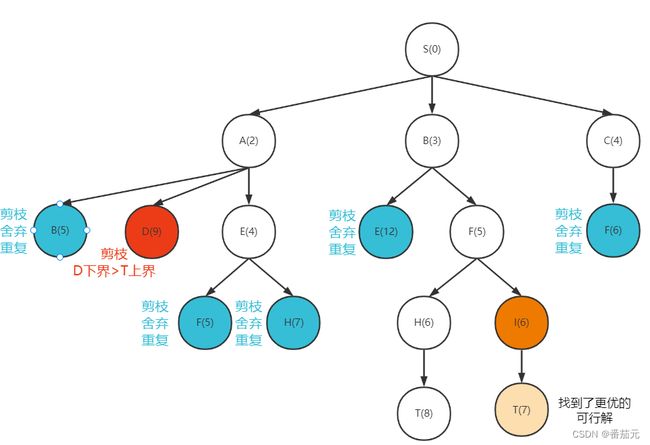
例题： 以八数码为例，使用优先队列（小顶堆）

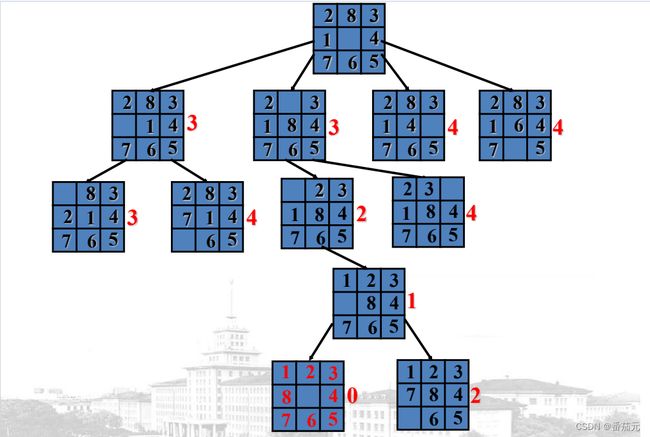
贪心的选择队列中的元素做搜索

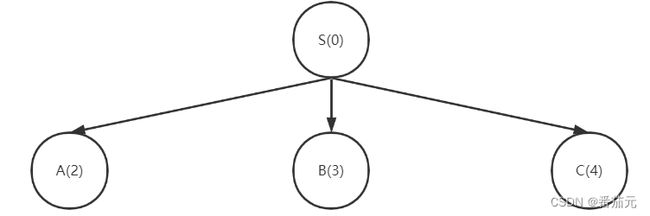
• 开始根节点入队，与目标情况差距为3，即1，2，8不在正确的位置上

[3(一层一号)]

• 根节点出队，将其子节点放入优先队列

[3(二层一号), 3(二层二号), 4(二层三号), 4(二层四号)]

• 取出 3(二层一号) ，将其子节点放入优先队列

[3(二层二号), 3(三层层二号), 4(二层三号), 4(二层四号), 4(三层一号)]

• 取出 3(二层二号) ，将其子节点放入优先队列

[2(三层三号), 3(三层层二号), 4(二层三号), 4(二层四号), 4(三层一号), 4(三层四号)]

• 取出 2(三层三号), 将其子节点放入优先队列

[1(四层一号), 3(三层层二号), 4(二层三号), 4(二层四号), 4(三层一号), 4(三层四号)]

• 取出 1(四层一号), 在其子节点中找到目标节点， 0(五层一号)，找到可行解，搜索停止

可以看到 Best-first search 并没有剪枝操作，只是贪心的选择搜索的下一个节点，找到的可能是局部最优解。

4. 代价一致搜索（Dijkstra）

代价一致搜索其实就是 Dijkstra 其搜索过程如下图所示

与 Best-first search 不一样的地方:

• 这里寻找点，用到的是从起点到当前点的距离
• 这里不限制每个节点的访问次数，找到一个更优的解，就可以去更新所有已经搜索过的路径长度，最后获得全局最优解。

伪代码（Pseudocode）如下

dist[u] 是从源点到顶点 u 的当前距离。

Graph.Edges(u, v) 返回连接两个邻居节点 u 和 v 的边的长度（即之间的距离）

 1  function Dijkstra(Graph, source):
 2      
 3      for each vertex v in Graph.Vertices:
 4          dist[v] ← INFINITY
 5          prev[v] ← UNDEFINED
 6          add v to Q
 7      dist[source] ← 0
 8      
 9      while Q is not empty:
10          u ← vertex in Q with min dist[u]
11          remove u from Q
12          
13          for each neighbor v of u still in Q:
14              alt ← dist[u] + Graph.Edges(u, v)
15              if alt < dist[v]:
16                  dist[v] ← alt
17                  prev[v] ← u
18
19      return dist[], prev[]

可以看到，一个节点可以多次入队，可以反复更新之前搜索过的路径，最后获得全局最优解。

5. 分支限界（Branch and bound，简称BB）

分支限界法常以广度优先或以最小耗费（最大效益）优先的方式搜索问题的解空间树。在分支限界法中，每一个活结点（没被访问过的节点）只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点。在这些儿子结点中，导致不可行解或导致非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中。此后，从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。

首先对比一下回溯法和分支限界法

• 回溯法：一种基于深度优先搜索的剪枝策略

  • 回溯法的求解目标是找出解空间树中满足约束条件的所有解

  • 利用深度优先搜索的方法，当搜到一个显然不合理的结果时，没必要继续深入搜索，这时利用回溯回退到其父节点，寻找下一个值得继续搜索的节点。如此可以剪去一些不必要的搜索，同时可以找到所有可能的结果。

• 分支限界法：常基于广度优先搜索的剪枝策略

  • 分支限界法的求解目标是找出满足约束条件的一个解，或是在满足约束条件的解中找出在某种意义下的最优解。
  • 利用广度优先搜索，首先根据已知的条件确定到达目标节点的代价上界，并估计当前可达拓展节点的代价下界，如果可拓展节点的代价下界超出到达目标节点的代价上界时，该节点肯定不是最优解了，抛弃之，即剪枝。
  • 实现方法可以有很多，原理差不多，一般选用优先队列，比较简单好理解
    • 队列式(FIFO)分支限界法：按照队列先进先出（FIFO）原则选取下一个节点为扩展节点。
    • LC（最小代价）分支限界法：采用优先队列作为活结点表
    • 栈式(LIFO)分支限界法：按照栈的存储方式排序拓展节点

例题：以单源最短路为例来解释分支界限法的计算过程：求从S->T的最短距离（括号内为从起点到达当前点的路径长度）

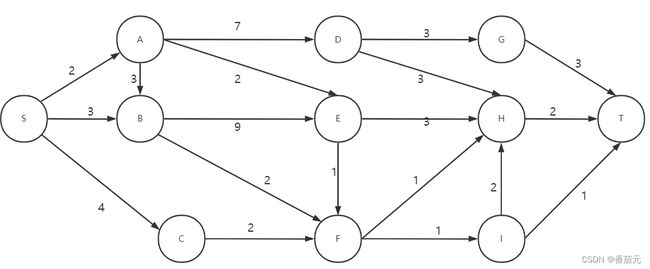
• 首先根节点（出发点）进入优先队列

[S(0)]

• 根节点出队，拓展根节点，将其可达的三个子节点入队
  

[A(2), B(3), C(4)]:此时S->A的代价最小，所以优先队列队首（堆顶）是A节点

• 队首A节点出队，拓展A节点，其子节点入队
  
  由于每个节点只能拓展一次，当出现两个相同可拓展节点时，即将出现重复的搜索，此时进行对重复搜索的剪枝，选择代价最优的拓展，这里舍弃路径较长的 B(5) ，即更新 B 节点的代价下界为 3。（当出现代价小于 3 的 B 节点，则更新 B 节点的最小下界，并替换 B 节点，否则丢弃新找到的节点）

[B(3), C(4), D(9), E(4)]

• 取出此时代价最小的节点 B 做拓展
  
  E 节点的下界此时为 4 ，剪枝舍弃新的节点 E(12)

[C(4), D(9), E(4), F(5)]

• 取出此时代价最小的节点 C 做拓展
  
  F 节点的下界此时为 5 ，剪枝舍弃新的节点 F(6)

[D(9), E(4), F(5)]

• 取出此时代价最小的节点 E 做拓展
  

[D(9), F(5), H(7)]

• 取出此时代价最小的节点 F 做拓展
  
  更新 H 下界为 6，舍弃原来的 H(7)

[D(9), H(6), I(6)]

• 取出此时代价最小的节点 H 做拓展
  
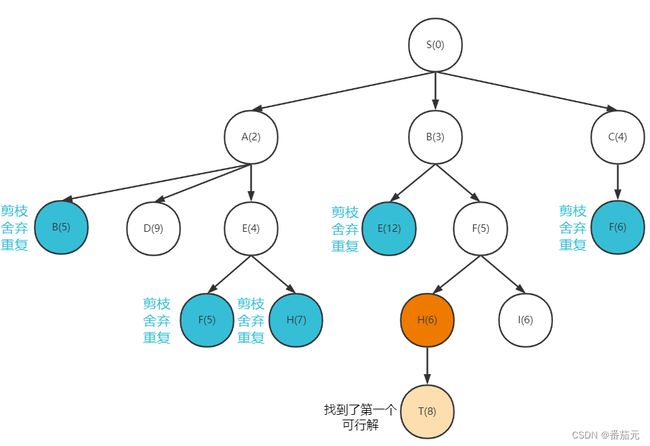
  这里贪心的找到了第一个可行解，记录从起点到达终点的代价上界为 8 。（此时如果再出现下界小于上界的节点，则直接抛弃，这部分是舍弃不必要搜索的剪枝）
  
  这里把 D(9) 分支剪掉，因为 D 此时的代价下界已是 9，超过起点到达目标点的上界，不可能找到更优的解，直接舍弃该分支。

[I(6)]

• 取出此时代价最小的节点 I 做拓展
  
  找到一个更优的可行解，更新起点到终点的上界为 7

此时优先队列为空，搜索结束，最短路径长为 7

6. 动态规划（Dynamic programming）

动态规划在查找有很多重叠子问题的情况的最优解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题，它们的结果都逐渐被计算并被保存，从简单的问题直到整个问题都被解决。因此，动态规划保存递归时的结果，因而不会在解决同样的问题时花费时间。

动态规划只能应用于有最优子结构的问题。最优子结构的意思是局部最优解能决定全局最优解（对有些问题这个要求并不能完全满足，故有时需要引入一定的近似）。简单地说，问题能够分解成子问题来解决。

例题1（无向图）： 以下图为例，求解 S->T 的最短路径

首先考虑如何拆解问题，

从一个点到达另一个点只有两种方式：

• 直接到达
• 通过其他点中转到达

想知道 S->T 的最短距离，对于他们路径上某个点 x ，只需要知道 S->X 的最小距离和 X->T 的最小距离，即可推出经过点 X 的情况下，S->T 的最短距离。

邻接矩阵：dp[i][j] 表示 i->j 的路径距离

状态转移方程如下：取当前的最短路径和经过 X 中转之后的最短路径中的最小值

dp[S][T] = min(dp[S][T], dp[S][X] + dp[X][T]);

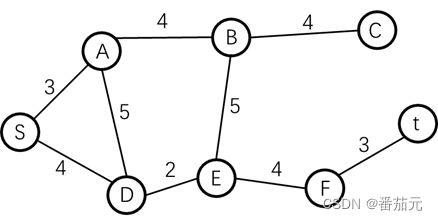
根据上图可以的到的邻接矩阵如下

• 0 表示 节点到自己距离为 0
• 空表示 dist[i][j] = inf 即 i, j 两点之间不可达，距离为无穷大
• 其余数字代表 dist[i][j] 即 i->j 的边长距离

i\j	S	A	B	C	D	E	F	t
S	0	3			4
A	3	0	4		5
B		4	0	4		5
C			4	0
D	4	5			0	2
E					2	0	4
F						4	0	3
t							3	0

动态规划过程如下：

首先初始化所有的 dp[i][j] 为当前邻接矩阵中的值

从目标结论出发，逐步递推，就可将问题转化到我们已知的初始值上，即 dp[S][A] 和 dp[S][D]

S->t : dp[S][t] = min(dp[S][t], dp[S][K] + dp[K][t]); K 可能是剩余节点中任何一个可能到达 t 的节点

S->F : dp[S][F] = min(dp[S][F], dp[S][K] + dp[K][F]); K 可能是剩余节点中任何一个可能到达 F 的节点

S->E : dp[S][E] = min(dp[S][E], dp[S][K] + dp[K][E]); K 可能是剩余节点中任何一个可能到达 E 的节点

…

S->A : dp[S][A] = min(dp[S][A], dp[S][K] + dp[K][A]); K 只能是 S ， 此时得到 dp[S][A] = 3;

S->D : dp[S][D] = min(dp[S][D], dp[S][K] + dp[K][D]); K 只能是 S ， 此时得到 dp[S][D] = 4;

那么我们从下向上递推，就能通过逐步更新到达前面节点的最小距离，得到我们要的答案 dp[S][T]

for (int t = 0; t < n; t++) { // 按邻接表中的顺序给搜索树编号
	for (int k = 0; k < t; k++) {
		dp[0][t] = min(dp[0][t], dp[0][k] + dp[k][t]);
	}
}

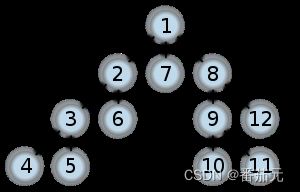
递推的过程可以看作从前往后建立一颗搜索树（不能抵达待更新路径终点的节点没有画出），下图的 g = dp[0][i]

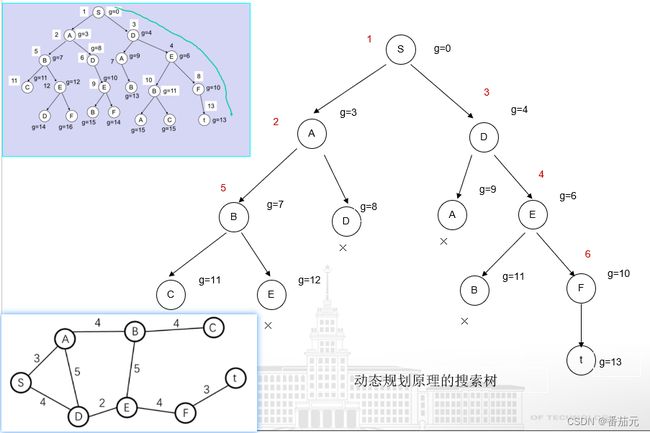
有多条路径能够到达某个节点时，在动态规划的过程中，已经将最短路径做了更新，之后每次用到的都是当前已知路径中最短的路径，相当对那些较长的路径做了剪枝，保留最短路径而删去之前找到的较长路径，不从这些路径继续向下寻找。

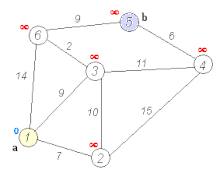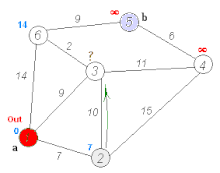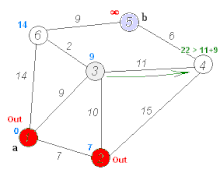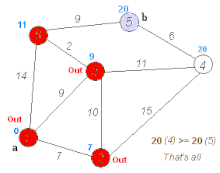
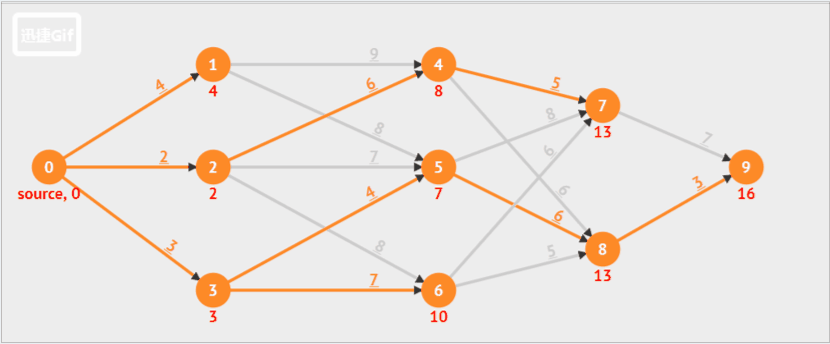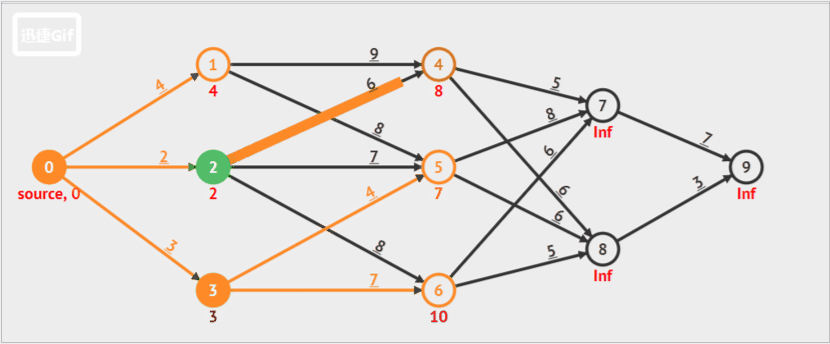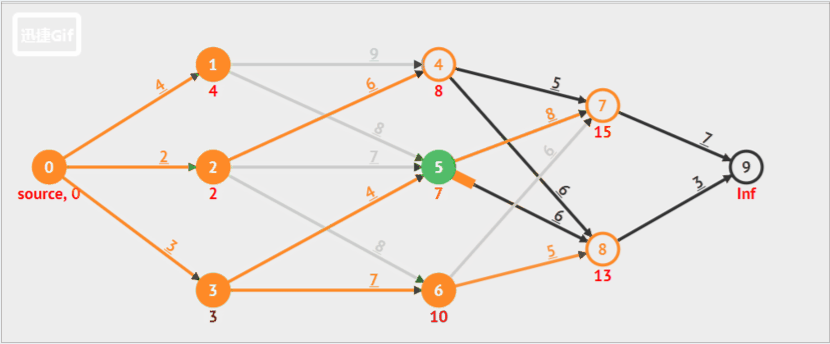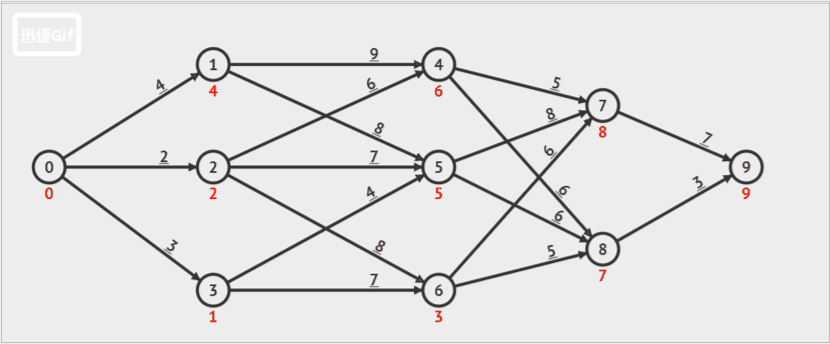
例题2（有向图，）： 一张来自阿里云社区的博客动图

如果拓展表中有多条到达某一公共节点的路径时，只保留耗散值最小的路径，其余删去。

下图橙色箭头就是在拓展节点，当拓展到的节点已经有可达路径时，判断新的路径和之前的路径哪个耗散值最小（即路径长度最小），保留最小长度的路径，其余路径删去，之后的拓展，基于这个最短的路径值继续拓展。

邻接矩阵：dist[i][j] 表示 i->j 的路径距离

dp[i] 表示从起点到达节点 i 的最小距离

状态转移方程如下：取当前的最短路径和经过 X 中转之后的最短路径中的最小值

dp[T] = min(dp[T], dp[X] + dist[X][T]);

动态规划核心代码

for (j = 1; j < n; j++) { // 首先以第一个点作为终点，从前往后递推，不断把终点后移直到终点，其之前的节点的路径已经都算出来了，可作为动态规划的条件
    for (i = j - 1; i >= 0; i--) {
        if (dist[i][j] + dp[i] < dp[j]) {
            dp[j] = dist[i][j] + dp[i];
        }
    }
}
return dp[n];

参考文章

Depth-First-Search

Breadth-first search

Hill climbing

Best-first search

Dijkstra’s algorithm

Branch and bound

Dynamic programming

七七八八百

快懂百科

阿里云社区