【LeetCode算法系列题解】第26~30题
CONTENTS
-
- LeetCode 26. 删除有序数组中的重复项(简单)
- LeetCode 27. 移除元素(简单)
- LeetCode 28. 找出字符串中第一个匹配项的下标(简单)
- LeetCode 29. 两数相除(中等)
- LeetCode 30. 串联所有单词的子串(困难)
LeetCode 26. 删除有序数组中的重复项(简单)
【题目描述】
给你一个升序排列的数组 nums,请你原地删除重复出现的元素,使每个元素只出现一次,返回删除后数组的新长度。元素的相对顺序应该保持一致。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k,你需要做以下事情确保你的题解可以被通过:
- 更改数组
nums,使nums的前k个元素包含唯一元素,并按照它们最初在nums中出现的顺序排列。nums的其余元素与nums的大小不重要。 - 返回
k。
【示例1】
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
【示例2】
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
【提示】
1 ≤ n u m s . l e n g t h ≤ 3 ∗ 1 0 4 1\le nums.length\le 3 * 10^4 1≤nums.length≤3∗104
− 1 0 4 ≤ n u m s [ i ] ≤ 1 0 4 -10^4\le nums[i]\le 10^4 −104≤nums[i]≤104
nums 已按升序排列
【分析】
本题使用 unique 函数一行就能搞定,该函数能够将数组的重复元素移至末端,返回不重复数组的最后一个元素的下一个迭代器,例如原数组为 nums = { 1, 1, 2, 2, 2, 3 },经 unique 处理后即变为 { 1, 2, 3, _, _, _ },返回值为 3 的下一个迭代器,减去 nums.begin() 后即为不重复数组中元素的数量。
我们也可以自己实现,使用两个指针,其中一个指针用来遍历每个数,当遍历到的数与前一个不同时就将该数存入另一个指针指向的位置,同时另一个指针向后移动一位。
【代码】
【unique 函数实现】
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
return unique(nums.begin(), nums.end()) - nums.begin();
}
};
【手动实现】
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int k = 0;
for (int i = 0; i < nums.size(); i++)
if (!i || nums[i] != nums[i - 1]) nums[k++] = nums[i];
return k;
}
};
LeetCode 27. 移除元素(简单)
【题目描述】
给你一个数组 nums 和一个值 val,你需要原地移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O ( 1 ) O(1) O(1) 额外空间并原地修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
【示例1】
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
【示例2】
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
【提示】
0 ≤ n u m s . l e n g t h ≤ 100 0\le nums.length\le 100 0≤nums.length≤100
0 ≤ n u m s [ i ] ≤ 50 0\le nums[i]\le 50 0≤nums[i]≤50
0 ≤ v a l ≤ 100 0\le val\le 100 0≤val≤100
【分析】
与上一题类似,本题同样可以使用 remove 函数将某个值全部移动到数组末端,并返回删除该数后数组的最后一个元素的下一个迭代器,减去 nums.begin() 即为删除该数后数组的长度。
我们也可以使用两个指针,其中一个遍历所有元素,当该元素不等于 val 时将其保存到另一个指针指向的位置,同时另一个指针向后移动一位。
【代码】
【remove 函数实现】
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
return remove(nums.begin(), nums.end(), val) - nums.begin();
}
};
【手动实现】
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int k = 0;
for (int i = 0; i < nums.size(); i++)
if (nums[i] != val) nums[k++] = nums[i];
return k;
}
};
LeetCode 28. 找出字符串中第一个匹配项的下标(简单)
【题目描述】
给你两个字符串 haystack 和 needle,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1。
【示例1】
输入:haystack = "sadbutsad", needle = "sad"
输出:0
解释:"sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ,所以返回 0 。
【示例2】
输入:haystack = "leetcode", needle = "leeto"
输出:-1
解释:"leeto" 没有在 "leetcode" 中出现,所以返回 -1 。
【提示】
1 ≤ h a y s t a c k . l e n g t h , n e e d l e . l e n g t h ≤ 1 0 4 1\le haystack.length, needle.length\le 10^4 1≤haystack.length,needle.length≤104
haystack 和 needle 仅由小写英文字符组成
【分析】
可以直接使用 find 函数查找子串第一次出现的位置,若不匹配则返回 -1。
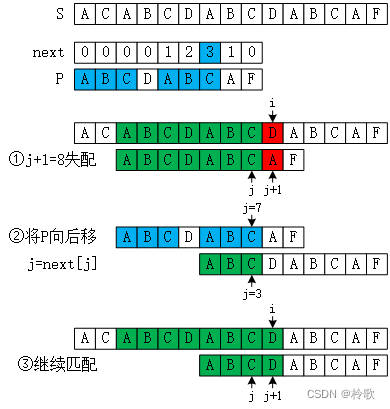
当然我们重点是要讲一下 KMP 算法。假设 S 为模板串(即较长的串),P 为模式串(即较短的串),KMP 中最重要的一个数组为 next[i],表示所有 P[1 ~ i] 的相等的前缀与后缀中长度的最大值(不考虑整个字符串作为前后缀)。KMP 算法流程如下图所示:
- 假设当前
S的指针 i i i 指向的字符失配了,P对应的指针为 j + 1 j+1 j+1,此时我们知道P[1 ~ j] == S[3 ~ i - 1]; P在 j j j 处的最长相同前后缀的长度为3(蓝色标注),说明P[1 ~ 3] == P[j - 2 ~ j];- 根据
P[j - 2 ~ j]已经和S[i - 3 ~ i - 1]匹配了可得P[1 ~ 3]也与S[i - 3 ~ i - 1]匹配; - 因此我们将
P向后移,令j = next[j],此时 j = 3 j=3 j=3; - 继续判断 j + 1 j+1 j+1 是否与 i i i 匹配。
【代码】
【find 函数实现】
class Solution {
public:
int strStr(string haystack, string needle) {
return haystack.find(needle);
}
};
【手动实现】
class Solution {
public:
int strStr(string s, string p) {
int n = s.size(), m = p.size();
s = ' ' + s, p = ' ' + p; // 调整为下标从1开始
vector<int> next(m + 1);
for (int i = 2, j = 0; i <= m; i++) // next[1]=0
{
while (j && p[i] != p[j + 1]) j = next[j];
if (p[i] == p[j + 1]) j++;
next[i] = j;
}
for (int i = 1, j = 0; i <= n; i++)
{
while (j && s[i] != p[j + 1]) j = next[j];
if (s[i] == p[j + 1]) j++;
if (j == m) return i - m; // 由于下标从1开始因此起始位置为i-m
}
return -1;
}
};
LeetCode 29. 两数相除(中等)
【题目描述】
给你两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和取余运算。
整数除法应该向零截断,也就是截去(truncate)其小数部分。例如,8.345 将被截断为 8,-2.7335 将被截断至 -2。
返回被除数 dividend 除以除数 divisor 得到的商。
注意:假设我们的环境只能存储 32 位有符号整数,其数值范围是 [ − 2 31 , 2 31 − 1 ] [-2^{31}, 2^{31} - 1] [−231,231−1]。本题中,如果商严格大于 2 31 − 1 2^{31} - 1 231−1,则返回 2 31 − 1 2^{31} - 1 231−1;如果商严格小于 − 2 31 -2^{31} −231,则返回 − 2 31 -2^{31} −231。
【示例1】
输入: dividend = 10, divisor = 3
输出: 3
解释: 10/3 = 3.33333.. ,向零截断后得到 3 。
【示例2】
输入: dividend = 7, divisor = -3
输出: -2
解释: 7/-3 = -2.33333.. ,向零截断后得到 -2 。
【提示】
− 2 31 ≤ d i v i d e n d , d i v i s o r ≤ 2 31 − 1 -2^{31}\le dividend, divisor\le 2^{31} - 1 −231≤dividend,divisor≤231−1
d i v i s o r ≠ 0 divisor\ne 0 divisor=0
【分析】
假设被除数为 x x x,除数为 y y y,第一个能想到的方法就是用 x x x 减 y y y 直到减不了为止,但是这种做法会超时。
假设 x y = k \frac {x}{y}=k yx=k,我们将 k k k 用二进制表示,假设是 ( 110010 ) 2 (110010)_2 (110010)2,也就是 2 1 + 2 4 + 2 5 2^1+2^4+2^5 21+24+25,即 x = 2 1 y + 2 4 y + 2 5 y x=2^1y+2^4y+2^5y x=21y+24y+25y。那么我们可以先预处理出 2 0 y , 2 1 y , … , 2 31 y 2^0y,2^1y,\dots ,2^{31}y 20y,21y,…,231y,然后从大到小枚举,若 x ≥ 2 i y x\ge 2^iy x≥2iy,那么就将 x x x 减去 2 i y 2^iy 2iy,并将商加上 2 i 2^i 2i。
对于正负的判断,我们可以先判断商的正负,然后将两个数统一转换成正数进行运算,最后再改变商的正负号。
【代码】
class Solution {
public:
int divide(int x, int y) {
vector<long long> exp; // 表示2^i * y
bool minus = (x > 0 && y < 0 || x < 0 && y > 0) ? true : false; // 商是否为负
long long a = abs((long long)x), b = abs((long long)y);
for (long long i = b; i <= a; i += i) exp.push_back(i); // 预处理
long long res = 0;
for (int i = exp.size() - 1; i >= 0; i--) // 从大到小枚举
if (a >= exp[i]) a -= exp[i], res += 1ll << i; // 记得加long long,左移可能会越界
if (minus) res = -res;
if (res > INT_MAX) return INT_MAX;
return res;
}
};
LeetCode 30. 串联所有单词的子串(困难)
【题目描述】
给定一个字符串 s 和一个字符串数组 words。words 中所有字符串长度相同。
s 中的串联子串是指一个包含 words 中所有字符串以任意顺序排列连接起来的子串。
例如,如果 words = ["ab","cd","ef"],那么 "abcdef","abefcd","cdabef","cdefab","efabcd",和 "efcdab" 都是串联子串。"acdbef" 不是串联子串,因为他不是任何 words 排列的连接。
返回所有串联子串在 s 中的开始索引。你可以以任意顺序返回答案。
【示例1】
输入:s = "barfoothefoobarman", words = ["foo","bar"]
输出:[0,9]
解释:因为 words.length == 2 同时 words[i].length == 3,连接的子字符串的长度必须为 6。
子串 "barfoo" 开始位置是 0。它是 words 中以 ["bar","foo"] 顺序排列的连接。
子串 "foobar" 开始位置是 9。它是 words 中以 ["foo","bar"] 顺序排列的连接。
输出顺序无关紧要。返回 [9,0] 也是可以的。
【示例2】
输入:s = "wordgoodgoodgoodbestword", words = ["word","good","best","word"]
输出:[]
解释:因为 words.length == 4 并且 words[i].length == 4,所以串联子串的长度必须为 16。
s 中没有子串长度为 16 并且等于 words 的任何顺序排列的连接。
所以我们返回一个空数组。
【示例3】
输入:s = "barfoofoobarthefoobarman", words = ["bar","foo","the"]
输出:[6,9,12]
解释:因为 words.length == 3 并且 words[i].length == 3,所以串联子串的长度必须为 9。
子串 "foobarthe" 开始位置是 6。它是 words 中以 ["foo","bar","the"] 顺序排列的连接。
子串 "barthefoo" 开始位置是 9。它是 words 中以 ["bar","the","foo"] 顺序排列的连接。
子串 "thefoobar" 开始位置是 12。它是 words 中以 ["the","foo","bar"] 顺序排列的连接。
【提示】
1 ≤ s . l e n g t h ≤ 1 0 4 1\le s.length\le 10^4 1≤s.length≤104
1 ≤ w o r d s . l e n g t h ≤ 5000 1\le words.length\le 5000 1≤words.length≤5000
1 ≤ w o r d s [ i ] . l e n g t h ≤ 30 1\le words[i].length\le 30 1≤words[i].length≤30
words[i] 和 s 由小写英文字母组成
【分析】
根据本题的数据量,如果直接暴力求解时间复杂度特别高,因此需要考虑一些优化。我们先记 n n n 为 s . s i z e ( ) s.size() s.size(), m m m 为 w o r d s . s i z e ( ) words.size() words.size(), w w w 为 w o r d s [ i ] . s i z e ( ) words[i].size() words[i].size()。
枚举 s s s 中所有长度为 m ∗ w m*w m∗w 的子串,我们按子串的起始位置划分为若干组,例如第一组中每个子串的起始位置分别为: 0 , w , 2 w , … , ( m − 1 ) w 0,w,2w,\dots ,(m-1)w 0,w,2w,…,(m−1)w,第二组中每个子串的起始位置分别为: 1 , w + 1 , 2 w + 1 , … , ( m − 1 ) w + 1 1,w+1,2w+1,\dots ,(m-1)w+1 1,w+1,2w+1,…,(m−1)w+1,以此类推,这样同一组里面划分出来的单词都是有规律的,而不是随机分割开的。对于第一组,我们从0开始按顺序枚举所有长度为 w w w 的单词子串,例如对于第一个样例,第一组的枚举顺序就是 bar/foo/the/foo/bar/man。
对于每一组,我们需要找到连续的 m m m 个区间,每个区间中的单词都存在于 words 中,因此我们可以用哈希表 window_cnt 维护一个长为 m m m 的滑动窗口中的 m m m 个单词的数量,然后每次都判断一下窗口中的 m m m 个单词是否都和 words 中的一一对应,但是每次我们不能都暴力判断,因此可以用 cnt 表示哈希表中为 words 中的单词的数量,当 cnt == m 时说明一一对应了。那么如何确定 cnt 呢?我们可以再用一个哈希表 words_cnt 表示 words 中每种单词的数量,当窗口新来了一个单词 t 时,window_cnt[t] 会加一,当 window_cnt[t] <= words_cnt[t] 时(表示 t 在 words 中出现过且在窗口中出现的次数还没超过 words 中 t 出现的次数),即可将 cnt 加一;当窗口移除一个单词 t 时,window_cnt[t] 会减一,当 window_cnt[t] < words_cnt[t] 时(表示 t 在 words 中出现过且当前窗口中的数量比 words 中少),即可将 cnt 减一。
对于第一个样例,第一组的求解过程如下:
[bar],滑动窗口长度还没超过 m m m,直接添加元素;[bar, foo],滑动窗口长度还没超过 m m m,直接添加元素,此时窗口中的内容和words一一对应,因此记录下答案;[foo, the],滑动窗口长度超过 m m m,先删除首部元素再添加,此时窗口中的内容与words不对应;[the, foo],同上;[foo, bar],此时窗口中的内容和words一一对应,记录答案;[bar, man],此时窗口中的内容与words不对应。
【代码】
class Solution {
public:
vector<int> findSubstring(string s, vector<string>& words) {
vector<int> res;
int n = s.size(), m = words.size(), w = words[0].size();
unordered_map<string, int> word_cnt; // 记录words中每个单词的数量
for (auto t: words) word_cnt[t]++;
for (int i = 0; i < w; i++)
{
unordered_map<string, int> window_cnt; // 滑动窗口中每个单词的数量
int cnt = 0; // 滑动窗口中为words中的单词的数量
for (int j = i; j <= n - w; j += w)
{
if (j >= i + m * w) // 超过滑动窗口的长度
{
string t = s.substr(j - m * w, w);
window_cnt[t]--;
if (window_cnt[t] < word_cnt[t]) cnt--; // words中不存在的单词数量为0
}
string t = s.substr(j, w);
window_cnt[t]++;
if (window_cnt[t] <= word_cnt[t]) cnt++; // 如果某个单词数量超过了也是错的
if (cnt == m) res.push_back(j - (m - 1) * w);
}
}
return res;
}
};