A. Increasing and Decreasing
题意:给出x, y, n,构造长度为n的递增数列使得 a1 = x, an = y, 并且相邻元素的差值递减。如果不能构造输出-1。
思路:如果能够构造出来,那么y - x的值应该大于 1 到 n - 1 的累加。构造时从y开始,依次向前 -1 -2 -3....即可。
AC代码
#include
#include
#include
#include
B. Swap and Reverse
题意:给定一个长度为n的字符串,可以进行两种操作:
1.交换  和
和 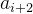 。
。
2.翻转 [i, i + k - 1] 区间的字符。
输出能够构造出的字典序最小的字符串。
思路:第一种操作只可以对奇偶性相同的字符进行操作,当 k 为奇数时,第二种操作同样只能对奇偶性相同的字符进行操作,当k为偶数时,第二种操作就可以改变字符位置的奇偶性。所以当 k 为偶数时,直接排序字符输出即可,当 k 为奇数时,对奇数序列和偶数序列分别排序输出。
AC代码
#include
#include
#include
#include
C. Divisor Chain
题意:给定一个数 x,每次只能减去它的除数,并且同一个除数最多用两次,直到减为一,输出每次变换后的序列。
思路:如果这个数是 2 的次幂,那么它只需要依次除 2 即可,例如 8 的输出为 8 4 2 1。如果不是 2 的次幂,可以考虑将他变为 2 的次幂,只需要减去二进制中除了第一位以外的 1 即可。例如 14 的二进制为 1110 ,那么我们只需依次减去 10 100 即可,(一个二进制数必定能整除最低位的1)。那14 的输出即为 14 12(-2) 8(-4) 4 2 1。
AC代码
#include
#include
#include
#include
D. Matrix Cascade
题意:给定一个n*n的矩阵,矩阵中的元素不是 0 就是 1,选定一个位置例如(i, j),那么以这个点为顶点做两条线,斜率为 1 和 -1,两条斜线以下的区域中的元素会翻转,问将矩阵全部变为0所需的最小操作。
思路:对于一个点(i, j),这个点以下的点是影响不到它的,所以对于(i, j),只考虑这个点以上的点即可。如果一个点进行了奇数次操作,那这个点会翻转,如果是偶数次就没有变化。所以遍历每一个点,如果这个点经过所有变化后仍为 1 ,那么此时只能改变这个点的值,答案就加一。至于如何记录上面点对下面点的影响, 我们可以维护两个前缀和数组,分别表示斜率为 1 和 -1。那么对于任一个点,只用考虑上方,左上方和右上方点的影响即可。
思路参考:http://t.csdn.cn/sHHfg
AC代码
#include
#include
#include
#include
![]() 和
和 ![]() 。
。