基于Python+TensorFlow+VAE变分编码器(Variational Auto-encoder)的智能图像生成——深度学习算法应用(含源码)+PPT

---

前言

这个项目采用了基于TensorFlow的全连接层神经网络模型，结合了VAE（Variational Auto-encoder）变分编码器技术，用于在FashionMNIST与MNIST数据集上实现数据的潜在空间学习和图像重构生成。

首先，我们利用TensorFlow构建了一个全连接层神经网络模型。这个模型具有多个神经元层，可以学习数据中的复杂关系和特征。

然后，我们引入了VAE变分编码器技术。VAE是一种生成模型，可以将数据映射到潜在空间，并通过随机性来实现数据的多样性。在这个项目中，我们将VAE应用于FashionMNIST与MNIST数据集，让模型学习如何将图像映射到潜在空间中的分布。

通过将图像编码为潜在空间中的分布，我们可以在潜在空间中进行操作和变换，然后使用解码器进行重构，生成新的图像。这意味着我们可以通过在潜在空间中进行插值、合成等操作来创造出与原始数据不同但又具有类似特征的图像。

综合上述步骤，我们的项目可以实现在FashionMNIST与MNIST数据集上的潜在空间学习和图像重构生成。这种方法不仅能够生成新的图像，还可以帮助我们更深入地理解数据的特征和分布，从而为图像生成和分析领域提供了一种有力的方法。

总体设计

本部分包括系统整体结构图和系统流程图。

系统整体结构图

系统整体结构如图所示。

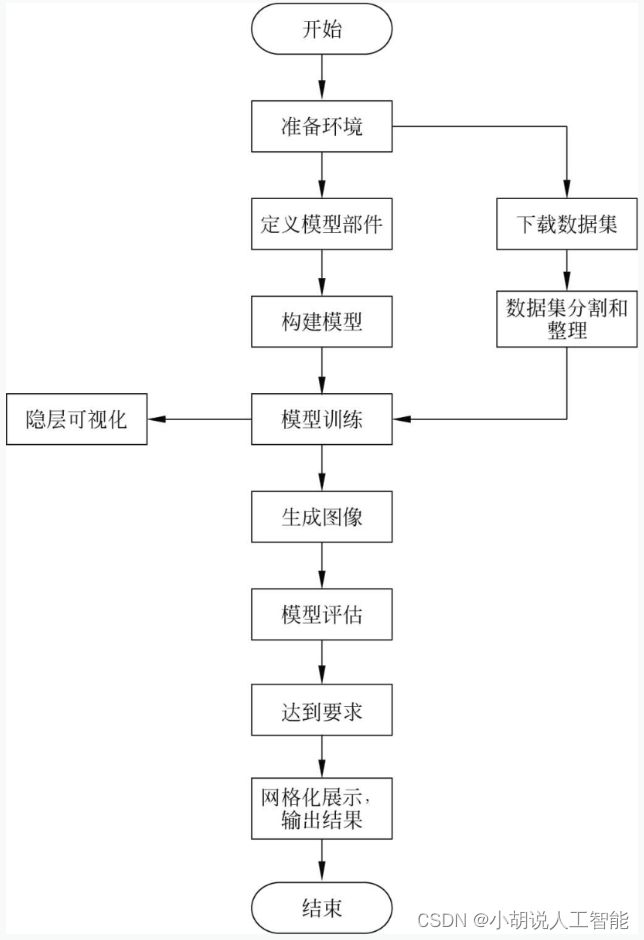
系统流程图

系统流程如图所示。

运行环境

本部分包括 Python 环境、TensorFlow 环境和 GPU 环境。

Python 环境

需要Python 3.6及以上配置，在Windows环境下下载Anaconda完成Python所需的配置。下载地址为https://www.anaconda.com/download/。根据操作系统进行选择，并使Python 3对应的Anaconda版本，也可以下载虚拟机在Linux环境下运行
代码。

TensorFlow环境

创建Python 3.5的环境，名称为TensorFlow:

conda create - n tensorflow python=3.5

此时Python版本和后面TensorFlow的版本有匹配问题，选择Python 3.x。有需要确认的地方，都按Y键。

在终端中激活TensorFlow环境:

Conda activate tensorflow

可用pip或conda安装Python包:

pip install tensorflow==1.9.0, keras=2.2.0

如果安装过慢，尝试使用国内源:

TensorFlow版本建议为1.9. 0, Keras版本建议为2.2.0

pip install tensorflow==1.9.0 keras==2.2.0 -i https://pypi.tuna.tsinghua.edu.cn/simple

Keras的backend可以是Theano或TensorFlow，为保持一致，将backend改为TensorFlow，编辑文件$HOME/.keras/keras.json ( 如果是Windows系统，则将$Home改为%USERPROFILE%)，修改backend字段即可， 改动始终有效:

{
"image_data.format": "channels_ last",
"epsilon": 1e-07,
"floatx": "float32",
"backend": "tensorflow"
}

或在代码中指定，仅对当前代码有效:

import os
os.environ['KERAS_BACKEND'] = 'tensorflow'
import keras

TensorFlow-GPU

本项目可以使用全连接层在CPU下进行训练。当然，如果你的电脑拥有GPU的话，可以稍微改动示例代码将全连接层换成CNN，CNN等神经网络模型使用GPU训练更快，

需要安装TensorFlow的GPU版本，命令如下:

pip install tensorflow-gpu

如果是Nvidia的GPU，还需要安装和配置CUDA和cuDNN，详细配置可以参考链接https://blog.csdn.net/qq_31136513/article/details/129859318。注意TensorFlow、CUDA、cuDNN之 间存在部分版本兼容问题。

模块实现

本项目包括4个模块:数据预处理、模型构建及编译、模型训练及图像生成、数据集处理。下面分别介绍各模块的功能及相关代码。

1. 数据预处理

在模型搭建和测试阶段使用MNIST手写数字数据集，下载地址为http://yann.lecun.com/exdb/mnist/。在模型的实际应用中，可以使用FashionMNIST数据集，下载地址为https://www.oschina.net/p/fashion-mnist。

FashionMNIST数据集的特点是数据量、数据形状、训练集和测试集分割完全仿照MNIST进行，针对其开发的模型可以零成本，使用MNIST手写数字数据集进行测试。MNIST是大型的手写数字(0~9) 数据集，包含大小为28X 28的图片70000张，其中包含60000张训练图片、10000张测试图片。相关代码如下:

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
%matplotlib inline
#加载MNIST数据集
#input_data脚本可用以下URL：
#https://raw.githubusercontent.com/tensorflow/tensorflow/master/tensorflow/examples/tutorials/mnist/input_data.py
import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
n_samples = mnist.train.num_examples
#输入层、全连接层、Lambda层
from keras.layers import Input, Dense, Lambda
from keras.models import Model
#引入后端
from keras import backend as K
#训练的目标函数
from keras import objectives

MNIST数据集准备成功，如图所示。

2. 模型构建及编译

数据载入VAE模型之后，定义参数，分别构建编码器、Lambda和解码器，再自定义总的损失函数并编译模型。

1.定义参数

相关代码如下:

#定义一些参数
#分批，每次训练100个
batch_size = 100
#MNIST中每张图片都为28 * 28的灰度图像
original_dim = 784   # 28 * 28
#使用全连接层，第一个输入为784，输出为256
intermediate_dim = 256
#第二个输入为256，输出维度是2
latent_dim = 2
#一共训练50轮
epochs = 50

2.构建模型

构建的VAE模型有3部分，分别为encoder、Lambda和decoder。encoder 是两层全连接层，隐层表示包括均值和方差。Lambda层不参与训练，只参与计算，用于后面产生新的参数。decoder也是两层全连接层，其中x_decoded_mean即为重构的输出(构建模型中的全连接层均可以替换为卷积层，但在CPU下的运行速度较慢)。相关代码如下:

#encoder部分，两层全连接层，隐层表示包括均值和方差
#输入数量不确定
x = Input(shape=(original_dim,))
#输出维度256
h = Dense(intermediate_dim, activation='relu')(x)
#隐层的均值和方差
z_mean = Dense(latent_dim)(h)
z_log_var = Dense(latent_dim)(h)
#Lambda层,不参与训练，只参与计算，用于后面产生新z参数
def sampling(args):
    z_mean, z_log_var = args
    #产生均值为0，方差为1的标准正态分布
    epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0.)
    #根据公式计算出新的正态分布
    return z_mean + K.exp(z_log_var / 2) * epsilon
#用Lambda函数产生新的z参数
z = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])
#decoder部分，两层全连接层，x_decoded_mean为重构的输出
#256个神经元
decoder_h = Dense(intermediate_dim, activation='relu')
#784个神经元
decoder_mean = Dense(original_dim, activation='sigmoid')
h_decoded = decoder_h(z)
#解码输出
x_decoded_mean = decoder_mean(h_decoded)

3.定义损失函数及模型编译

根据VAE原始论文给出的损失近似表达式，定义的损失函数vae_loss 由两部分构成，分别为二分类交叉熵xent_loss和KL散度kl_loss。 使用msprop优化算法完成模型编译。

相关代码如下:

def vae_loss(x, x_decoded_mean):
    #交叉熵
    xent_loss = original_dim * objectives.binary_crossentropy(x, x_decoded_mean)
    #KL散度
    kl_loss = -0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
    #得到vae_loss
    return xent_loss + kl_loss
vae = Model(x, x_decoded_mean)
#rmsprop优化算法
vae.compile(optimizer='rmsprop', loss=vae_loss)

3. 模型训练及图像生成

在数据集准备成功和模型构建编译完成之后，进行数据的加载并开始模型训练，包括编码器、生成器。与其他生成类模型相比，使用VAE可以得到隐层变量的分布情况，从而实现数据在隐层中的可视化。VAE通过对隐变量空间采样得到生成器的输入内容，对于二维的隐变量，用网格化的方法在二维空间采样，作为新的参数z输入生成器，最后将生成的样本以20X20的图像展示。

1.模型训练

相关代码如下：

#加载数据
(x_train, y_train), (x_test, y_test) = mnist.load_data()
#数据归一化到0~1区间
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
#数据维度60000×*84
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))
vae.fit(x_train, x_train,
        #打乱
        shuffle=True,
        #运行50次
        epochs=epochs,
        #batch_size为100
        batch_size=batch_size,
        validation_data=(x_test, x_test))

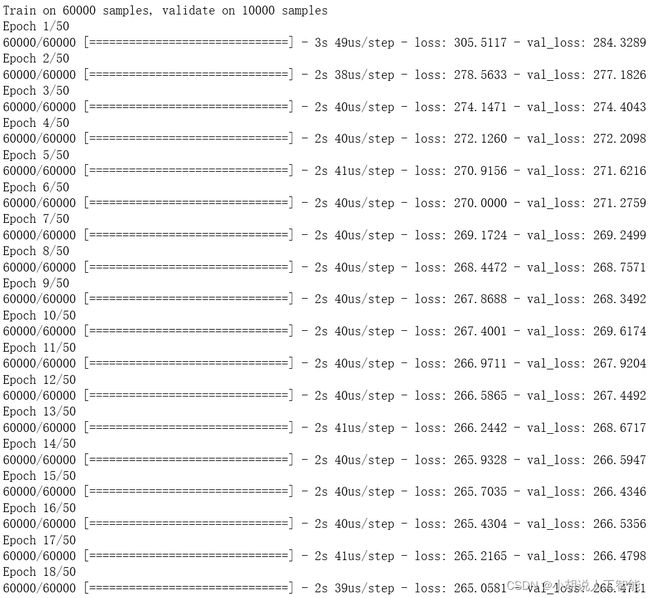
模型训练过程如图所示。

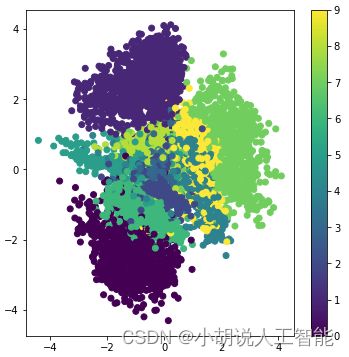
2.数据集的隐层可视化

完成模型训练后，输入数据集的分布特征，即可训练出隐层映射关系。构建数据集的隐层可视化模块便于观察数据集的特征，为研究提供便利。相关代码如下:

#定义一个encoder,实现MNIST中的数据在隐层中的可视化
encoder = Model(x, z_mean)
x_test_encoded = encoder.predict(x_test, batch_size=batch_size)
#图片大小为6*6
plt.figure(figsize=(6, 6))
#定义坐标，标签决定颜色
plt.scatter(x_test_encoded[:, 0], x_test_encoded[:, 1], c=y_test)
plt.colorbar()
plt.show()

3.生成图像

定义一个生成器，从隐层到输出，用于产生新的样本，并用网格化的方法产生一些二维数据，作为新的z参数输入生成器，将生成的x以20X20的图像展示。相关代码如下:

#加载数据
(x_train, y_train), (x_test, y_test) = mnist.load_data()
#数据归一化到0~1区间
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
#定义一个生成器，从隐层到输出，用于产生新的样本
decoder_input = Input(shape=(latent_dim,))
_h_decoded = decoder_h(decoder_input)
_x_decoded_mean = decoder_mean(_h_decoded)
#生成新的样本
generator = Model(decoder_input, _x_decoded_mean)
#用网格化的方法产生一些二维数据，作为新的z参数输入到生成器，并展示生成的x
#20*20个数字
n = 20
#数字大小28*28
digit_size = 28
figure = np.zeros((digit_size * n, digit_size * n))
#产生网格点
grid_x = np.linspace(-4, 4, n)
grid_y = np.linspace(-4, 4, n)
for i, xi in enumerate(grid_x):
    for j, yi in enumerate(grid_y):
        z_sample = np.array([[yi, xi]])
        x_decoded = generator.predict(z_sample)
        #784的向量变成28*28的平面二维数组
        digit = x_decoded[0].reshape(digit_size, digit_size)
        #将digit放入figure中对应的位置上去
        figure[(n - i - 1) * digit_size: (n - i) * digit_size,
               j * digit_size: (j + 1) * digit_size] = digit
plt.figure(figsize=(10, 10))
plt.imshow(figure)
plt.show()

4. 不同数据集处理

本部分包括MNIST和FashionMNIST数据集部分的代码。FashionMNIST对MNIST数据集的代码进行了优化，训练要求高、时间长。

1.MNIST数据集

相关代码如下：

#-*- coding: utf-8 -*-
#加载库
#引入numpy和matplotlib库
import numpy as np
import matplotlib.pyplot as plt
#输入层，全连接层，Lambda层
from keras.layers import Input, Dense, Lambda
from keras.models import Model
#引入后端
from keras import backend as K
#训练的目标函数
from keras import objectives
#数据集MINST
from keras.datasets import mnist
#定义一些参数
#分批，每次训练100个
batch_size = 100
#MNIST中每张图片都为28 * 28的灰度图像
original_dim = 784   # 28 * 28
#使用全连接层，第一个输入为784，输出为256
intermediate_dim = 256
#第二个输入为256，输出维度是2
latent_dim = 2
#一共训练50次
epochs = 50
#encoder部分，两层全连接层，隐层表示包括均值和方差
#输入数量不确定
x = Input(shape=(original_dim,))
#输出维度256
h = Dense(intermediate_dim, activation='relu')(x)
#隐层的均值和方差
z_mean = Dense(latent_dim)(h)
z_log_var = Dense(latent_dim)(h)
#Lambda层,不参与训练，只参与计算，用于后面产生新的z参数
def sampling(args):
    z_mean, z_log_var = args
    #产生100*2，均值为0，方差为1的标准正态分布
    epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0.)
    #根据公式计算出新的正态分布
    return z_mean + K.exp(z_log_var / 2) * epsilon
#用Lambda函数产生新的z参数
z = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])
#decoder部分，两层全连接层，x_decoded_mean为重构的输出
#256个神经元
decoder_h = Dense(intermediate_dim, activation='relu')
#784个神经元
decoder_mean = Dense(original_dim, activation='sigmoid')
h_decoded = decoder_h(z)
#解码输出
x_decoded_mean = decoder_mean(h_decoded)
#自定义总的损失函数并编译模型
def vae_loss(x, x_decoded_mean):
    #交叉熵
    xent_loss = original_dim * objectives.binary_crossentropy(x, x_decoded_mean)
    #KL散度
    kl_loss = -0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
    #得到vae_loss
    return xent_loss + kl_loss
vae = Model(x, x_decoded_mean)
#rmsprop优化算法
vae.compile(optimizer='rmsprop', loss=vae_loss)
#加载数据并训练
#加载数据
(x_train, y_train), (x_test, y_test) = mnist.load_data()
#数据归一化到0~1区间
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
#数据维度60000 * 784
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))
vae.fit(x_train, x_train,
        #打乱
        shuffle=True,
        #运行50次
        epochs=epochs,
        #batch_size为100
        batch_size=batch_size,
        validation_data=(x_test, x_test))
#定义一个encoder,实现MNIST中的数据在隐层中的可视化
encoder = Model(x, z_mean)
x_test_encoded = encoder.predict(x_test, batch_size=batch_size)
#图片大小为6*6
plt.figure(figsize=(6, 6))
#定义坐标，标签决定颜色
plt.scatter(x_test_encoded[:, 0], x_test_encoded[:, 1], c=y_test)
plt.colorbar()
plt.show()
#定义一个生成器，从隐层到输出，用于产生新的样本
decoder_input = Input(shape=(latent_dim,))
_h_decoded = decoder_h(decoder_input)
_x_decoded_mean = decoder_mean(_h_decoded)
#生成新的样本
generator = Model(decoder_input, _x_decoded_mean)
#用网格化的方法产生一些二维数据，作为新的z参数输入到生成器，并将生成的x展示出来
#20*20个数字
n = 20
#数字大小28*28
digit_size = 28
figure = np.zeros((digit_size * n, digit_size * n))
#产生网格点
grid_x = np.linspace(-4, 4, n)
grid_y = np.linspace(-4, 4, n)
for i, xi in enumerate(grid_x):
    for j, yi in enumerate(grid_y):
        z_sample = np.array([[yi, xi]])
        x_decoded = generator.predict(z_sample)
        #784的向量变成28*28的平面二维数组
        digit = x_decoded[0].reshape(digit_size, digit_size)
        #将digit放入figure中对应的位置上去
        figure[(n - i - 1) * digit_size: (n - i) * digit_size,
               j * digit_size: (j + 1) * digit_size] = digit
plt.figure(figsize=(10, 10))
plt.imshow(figure)
plt.show()

2. FashionMNIST数据集

FashionMNIST数据集如图所示：

相关代码如下：

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(0)
tf.set_random_seed(0)
#加载FashionMNIST数据
#input_data脚本可以参考如下URL:
#https://raw.githubusercontent.com/tensorflow/tensorflow/master/tensorflow/examples/tutorials/fashionmnist/input_data.py
import input_data
fashionmnist = input_data.read_data_sets('MNIST_data', one_hot=True)
n_samples = fashionmnist.train.num_examples
def xavier_init(fan_in, fan_out, constant=1): 
    """ Xavier初始化网络权重，参考
URL：
    https://stackoverflow.com/questions/33640581/how-to-do-xavier-initialization-on-tensorflow
"""
    low = -constant*np.sqrt(6.0/(fan_in + fan_out)) 
    high = constant*np.sqrt(6.0/(fan_in + fan_out))
    return tf.random_uniform((fan_in, fan_out), 
                             minval=low, maxval=high, 
                             dtype=tf.float32)
class VariationalAutoencoder(object):
    """
具有使用TensorFlow实现的类似sklearn接口的变体自动编码器（VAE）。该概率编码器和解码器使用高斯分布并由多层感知器实现，可以端到端学习VAE。有关信息，参见Kingma和Welling的"Auto-Encoding Variational Bayes"
    """
    def __init__(self, network_architecture, transfer_fct=tf.nn.softplus,                  learning_rate=0.001, batch_size=100):
        self.network_architecture = network_architecture
        self.transfer_fct = transfer_fct
        self.learning_rate = learning_rate
        self.batch_size = batch_size
        # tf图输入
self.x = tf.placeholder(tf.float32, [None, network_architecture["n_input"]])
        #创建自动编码器网络
        self._create_network()
        #定义基于损失函数的变分上限和相应的优化器
        self._create_loss_optimizer()
        #初始化变量
        init = tf.global_variables_initializer()
       #启动会话
        self.sess = tf.InteractiveSession()
        self.sess.run(init)
        def _create_network(self):
        #初始化自动编码网络权重和偏差 
       network_weights=self._initialize_weights(**self.network_architecture)
        #使用识别网络确定潜在空间中高斯分布的均值和（对数）方差
        self.z_mean, self.z_log_sigma_sq = \
            self._recognition_network(network_weights["weights_recog"], 
                                      network_weights["biases_recog"])
        #从高斯分布中得出z参数的一个样本
        n_z = self.network_architecture["n_z"]
        eps = tf.random_normal((self.batch_size, n_z), 0, 1, 
                               dtype=tf.float32)
        #z = mu + sigma*epsilon
        self.z = tf.add(self.z_mean, 
                        tf.mul(tf.sqrt(tf.exp(self.z_log_sigma_sq)), eps))
        #使用生成器确定重构输入伯努利分布的平均值
        self.x_reconstr_mean = \
            self._generator_network(network_weights["weights_gener"],
                                    network_weights["biases_gener"])
        def _initialize_weights(self, n_hidden_recog_1, n_hidden_recog_2, 
                            n_hidden_gener_1,  n_hidden_gener_2, 
                            n_input, n_z):
        all_weights = dict()
        all_weights['weights_recog'] = {
            'h1': tf.Variable(xavier_init(n_input, n_hidden_recog_1)),
        'h2': tf.Variable(xavier_init(n_hidden_recog_1, n_hidden_recog_2)),
            'out_mean': tf.Variable(xavier_init(n_hidden_recog_2, n_z)),
           'out_log_sigma':tf.Variable(xavier_init(n_hidden_recog_2, n_z))}
        all_weights['biases_recog'] = {
          'b1':tf.Variable(tf.zeros([n_hidden_recog_1], dtype=tf.float32)),
          'b2':tf.Variable(tf.zeros([n_hidden_recog_2], dtype=tf.float32)),
            'out_mean': tf.Variable(tf.zeros([n_z], dtype=tf.float32)),
            'out_log_sigma':tf.Variable(tf.zeros([n_z], dtype=tf.float32))}
        all_weights['weights_gener'] = {
            'h1': tf.Variable(xavier_init(n_z, n_hidden_gener_1)),
         'h2':tf.Variable(xavier_init(n_hidden_gener_1, n_hidden_gener_2)),
            'out_mean':tf.Variable(xavier_init(n_hidden_gener_2, n_input)),
       'out_log_sigma':tf.Variable(xavier_init(n_hidden_gener_2,n_input))}
        all_weights['biases_gener'] = {
         'b1': tf.Variable(tf.zeros([n_hidden_gener_1], dtype=tf.float32)),
         'b2': tf.Variable(tf.zeros([n_hidden_gener_2], dtype=tf.float32)),
          'out_mean': tf.Variable(tf.zeros([n_input], dtype=tf.float32)),
          'out_log_sigma': tf.Variable(tf.zeros([n_input], dtype=tf.float32))}
        return all_weights
          def _recognition_network(self, weights, biases):
        #生成概率编码器（识别网络），该编码器将输入映射到潜在空间中的正态分布
     layer_1 = self.transfer_fct(tf.add(tf.matmul(self.x, weights['h1']),                                            biases['b1'])) 
    layer_2 = self.transfer_fct(tf.add(tf.matmul(layer_1, weights['h2']),                                           biases['b2'])) 
        z_mean = tf.add(tf.matmul(layer_2, weights['out_mean']),
                        biases['out_mean'])
        z_log_sigma_sq = \
            tf.add(tf.matmul(layer_2, weights['out_log_sigma']), 
                   biases['out_log_sigma'])
        return (z_mean, z_log_sigma_sq)
    def _generator_network(self, weights, biases):
        #生成概率解码器（解码器网络），将潜在空间中的点映射到数据空间中的伯努利分布
     layer_1 = self.transfer_fct(tf.add(tf.matmul(self.z, weights['h1']),                                            biases['b1'])) 
     layer_2 = self.transfer_fct(tf.add(tf.matmul(layer_1,weights['h2']),                     biases['b2'])) 
        x_reconstr_mean = \
            tf.nn.sigmoid(tf.add(tf.matmul(layer_2, weights['out_mean']), 
                                 biases['out_mean']))
        return x_reconstr_mean
           def _create_loss_optimizer(self):
#损失由两部分组成：1）重建损失（在数据空间中，解码器在重建的伯努利分布下，输入的负对数概率），可以解释为当潜在激活被激活时重构输入所需的“nat”数
        #增加1e-10避免出现log(0.0)
        reconstr_loss = \
            -tf.reduce_sum(self.x * tf.log(1e-10 + self.x_reconstr_mean)
            + (1-self.x) * tf.log(1e-10 + 1 - self.x_reconstr_mean),
                           1)
#潜在损失，定义为编码器数据和某些先验数据之间，在潜在空间分布之间的Kullback Leibler散度，充当一种正则化，可以解释为在先验情况下传输潜在空间分布所需的“nat”数
        latent_loss = -0.5 * tf.reduce_sum(1 + self.z_log_sigma_sq 
                                           - tf.square(self.z_mean) 
                                           - tf.exp(self.z_log_sigma_sq), 1)
        self.cost = tf.reduce_mean(reconstr_loss + latent_loss)#平均化
         #使用ADAM优化器
        self.optimizer = \            tf.train.AdamOptimizer(learning_rate=self.learning_rate).minimize(self.cost)
        def partial_fit(self, X):
        #基于最小数据训练模型，返回最小批量代价
        opt, cost = self.sess.run((self.optimizer, self.cost), 
                                  feed_dict={self.x: X})
        return cost
        def transform(self, X):
        #将数据映射到潜在空间，映射到分布的均值，也可以从高斯分布中采样
        return self.sess.run(self.z_mean, feed_dict={self.x: X})
        def generate(self, z_mu=None):
"""
通过从潜在空间采样生成数据。如果z_mu不为None，则生成潜在空间中此点的数据，否则，z_mu是从潜在空间中的先验数据得出
"""
        if z_mu is None:
            z_mu = np.random.normal(size=self.network_architecture["n_z"])
        #映射到分布的均值，也可以从高斯分布中采样
        return self.sess.run(self.x_reconstr_mean, 
                             feed_dict={self.z: z_mu})
        def reconstruct(self, X):
        #使用VAE重建给定的数据
        return self.sess.run(self.x_reconstr_mean, 
                             feed_dict={self.x: X})
def train(network_architecture, learning_rate=0.001,
          batch_size=100, training_epochs=10, display_step=5):
    vae = VariationalAutoencoder(network_architecture, 
                                 learning_rate=learning_rate, 
                                 batch_size=batch_size)
    #循环训练
    for epoch in range(training_epochs):
        avg_cost = 0.
        total_batch = int(n_samples / batch_size)
        for i in range(total_batch):
            batch_xs, _ = fashionmnist.train.next_batch(batch_size)
            #使用批量数据进行拟合训练
            cost = vae.partial_fit(batch_xs)
            #计算平均损失
            avg_cost += cost / n_samples * batch_size
        #显示日志
        if epoch % display_step == 0:
            print("Epoch:", '%04d' % (epoch+1), 
                  "cost=", "{:.9f}".format(avg_cost))
    return vae
network_architecture = \
    dict(n_hidden_recog_1=500, #第一层编码器神经元
         n_hidden_recog_2=500,  #第二层编码器神经元
         n_hidden_gener_1=500,  #第一层解码器神经元
         n_hidden_gener_2=500,  #第二层解码器神经元
         n_input=784,             #FASHIONMNIST数据输入
         n_z=20)                   #潜在空间的维数
vae = train(network_architecture, training_epochs=75)
x_sample = fashionmnist.test.next_batch(100)[0]
x_reconstruct = vae.reconstruct(x_sample)
plt.figure(figsize=(8, 12))
for i in range(5):
    plt.subplot(5, 2, 2*i + 1)
    plt.imshow(x_sample[i].reshape(28, 28), vmin=0, vmax=1, cmap="gray")
    plt.title("Test input")
    plt.colorbar()
    plt.subplot(5, 2, 2*i + 2)
    plt.imshow(x_reconstruct[i].reshape(28, 28), vmin=0, vmax=1, cmap="gray")
    plt.title("Reconstruction")
    plt.colorbar()
plt.tight_layout()
network_architecture = \
    dict(n_hidden_recog_1=500, #第一层编码器神经元
         n_hidden_recog_2=500, #第二层编码器神经元
         n_hidden_gener_1=500, #第一层解码器神经元
         n_hidden_gener_2=500, #第二层解码器神经元
         n_input=784,  #FASHIONMNIST数据输入(28*28)
         n_z=2)  #潜在空间的维数
vae_2d = train(network_architecture, training_epochs=75)
x_sample, y_sample = fashionmnist.test.next_batch(5000)
z_mu = vae_2d.transform(x_sample)
plt.figure(figsize=(8, 6)) 
plt.scatter(z_mu[:, 0], z_mu[:, 1], c=np.argmax(y_sample, 1))
plt.colorbar()
plt.grid()
nx = ny = 20
x_values = np.linspace(-3, 3, nx)
y_values = np.linspace(-3, 3, ny)
canvas = np.empty((28*ny, 28*nx))
for i, yi in enumerate(x_values):
    for j, xi in enumerate(y_values):
        z_mu = np.array([[xi, yi]]*vae.batch_size)
        x_mean = vae_2d.generate(z_mu)
        canvas[(nx-i-1)*28:(nx-i)*28, j*28:(j+1)*28] = x_mean[0].reshape(28, 28)
plt.figure(figsize=(8, 10))        
Xi, Yi = np.meshgrid(x_values, y_values)
plt.imshow(canvas, origin="upper", cmap="gray")
plt.tight_layout()

系统测试

本部分包括隐层可视化、测试效果及放大图像。

1.隐层可视化

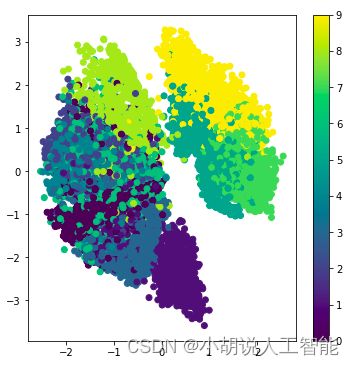
模型训练后每个数据都转换成一个二维的离散点在图像中呈现。离散点横纵坐标值是经模型训练后对应二维向量的值，离散点的颜色由数据对应的标签决定。MNIST数据集的隐层可视化如图1所示，同类数据绝大多数聚集在一起，证明VAE的训练结果比较理想。FashionMNIST数据集的隐层可视化如图2所示。

图1 MNIST隐层

图2 FashionMNIST隐层

2. 测试效果

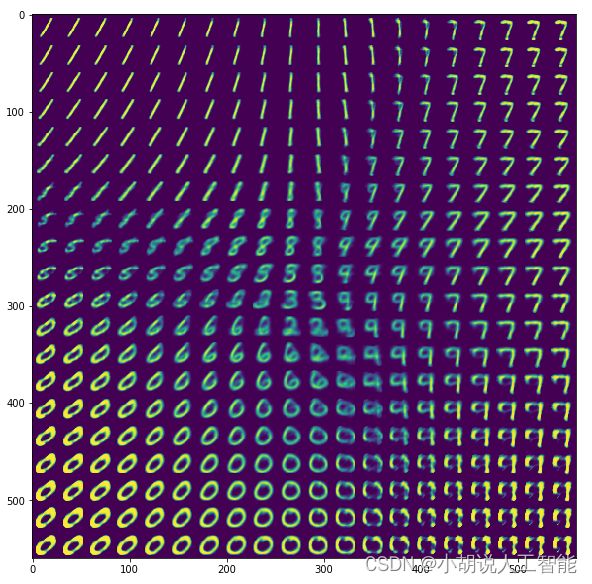
相对于黑底白字，为便于观察图像，进行热图绘制，生成20X20的数据集图像，如图所示。输入0~9的手写数据集时，VAE能清晰地生成各种数字。0、6、8、9等数字二进制形式中包含很多0的信息，所以生成的0较多；还生成很多数字1，可能1、2、6、7等数字二进制形式中包含很多1的信息。不仅如此，还生成一些无法辨认数字图片VAE是对数据集进行学习模仿从而生产新的数据，出现这种情况是合理的。数据集内图片间的差异越大，产生无法辨认的数字图片概率越大。

生成的每一个数据图像都是28X28像素的灰度图像，与输入数据集相同，如图所示。

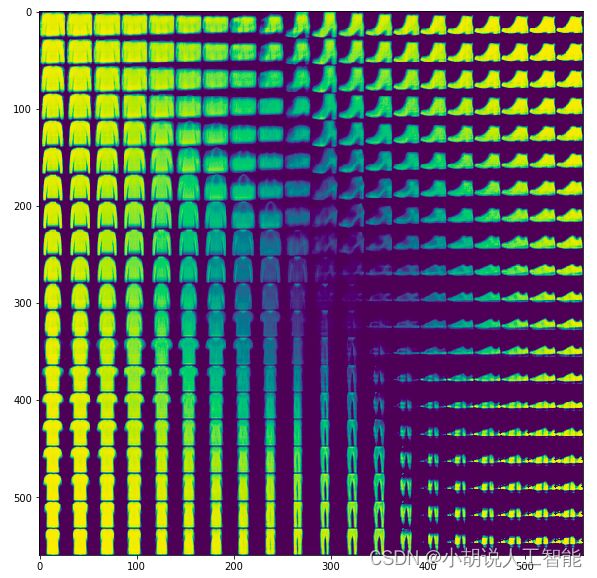
FashionMNIST的20 X 20像素数据集如图所示。

3. 放大图像

为实现放大图像，实验了插值放大方式和VAE-CPPN模型方式。插值放大方式采用TensorFlow提供的函数:

tf.image.resize()

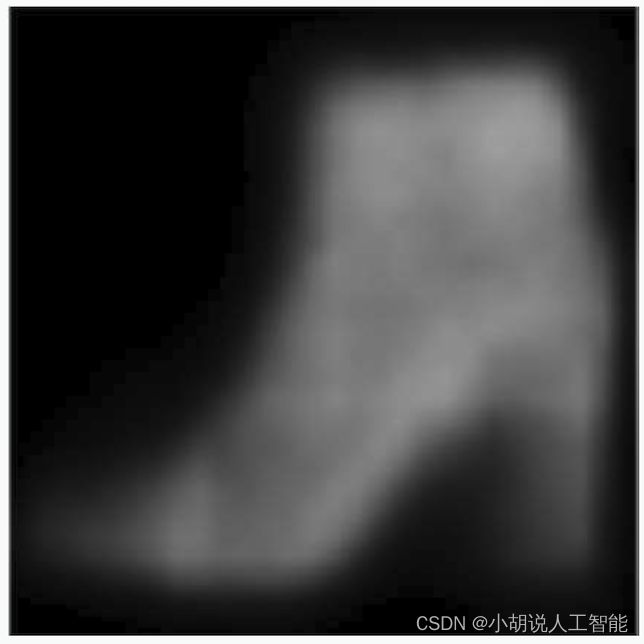
放大的图片仍然很模糊，因为VAE生成结果原本就相对模糊，效果如图所示。

为得到较为清晰的图像，在基础实验成功后重构了代码，将CPPN作为VAE解码器进行训练，放大效果如图所示。

工程源代码下载

详见本人博客资源下载页

---

其它资料下载

如果大家想继续了解人工智能相关学习路线和知识体系，欢迎大家翻阅我的另外一篇博客《重磅 | 完备的人工智能AI 学习——基础知识学习路线，所有资料免关注免套路直接网盘下载》
这篇博客参考了Github知名开源平台，AI技术平台以及相关领域专家：Datawhale，ApacheCN，AI有道和黄海广博士等约有近100G相关资料，希望能帮助到所有小伙伴们。